Презентация на тему Понятие обратной функции. Определение логарифмической функции

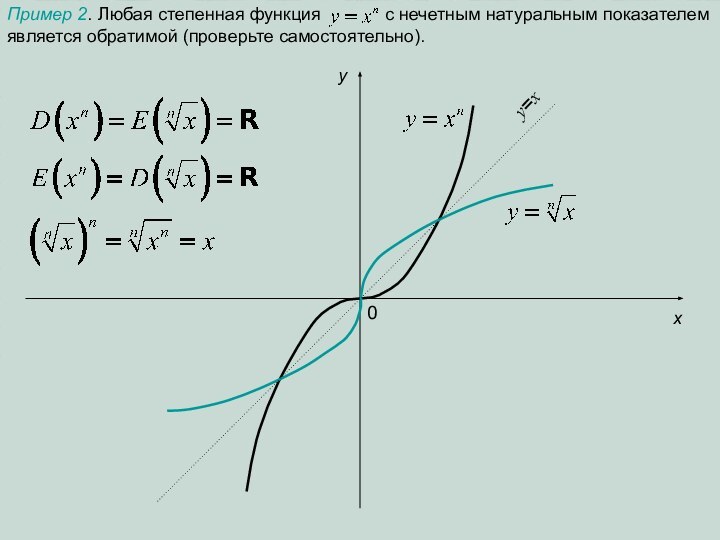
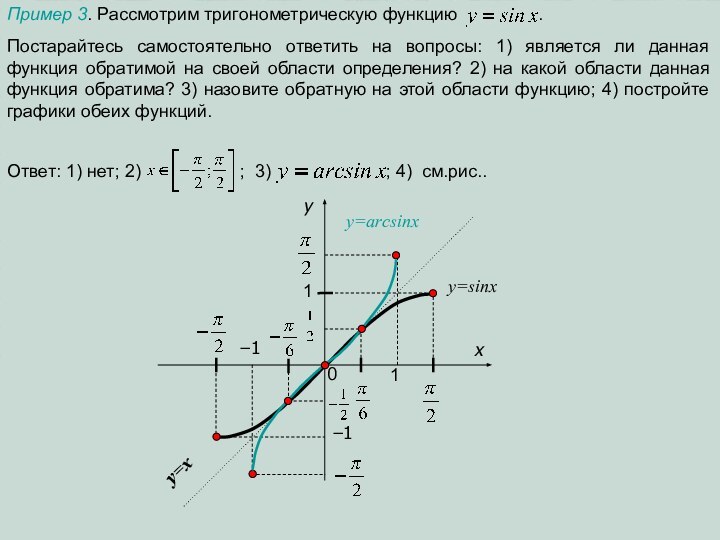
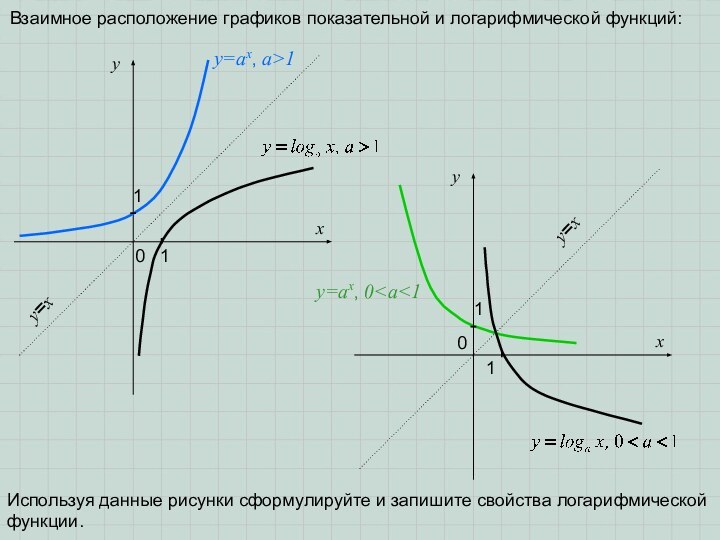
формулой y=f(x). Пусть, для определенности, это будет линейная функция

…Правильно: для этого надо данное значение аргумента подставить в формулу и произвести вычисления. Например, при x=2, значение функции равно y=22–7=–3.

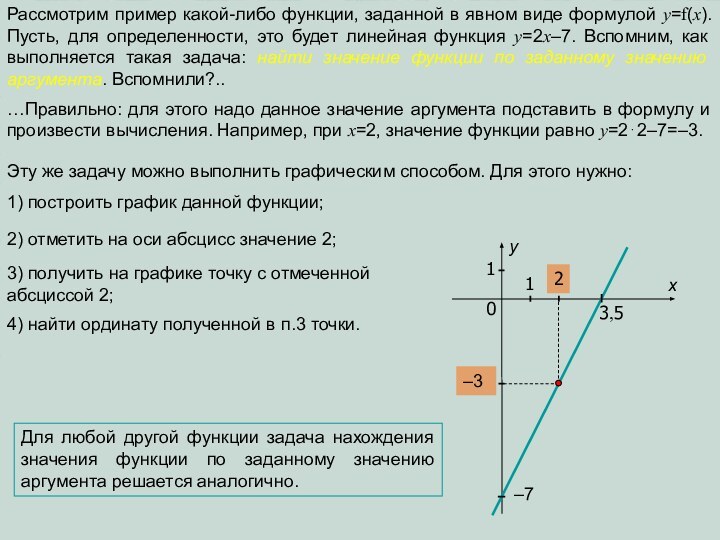
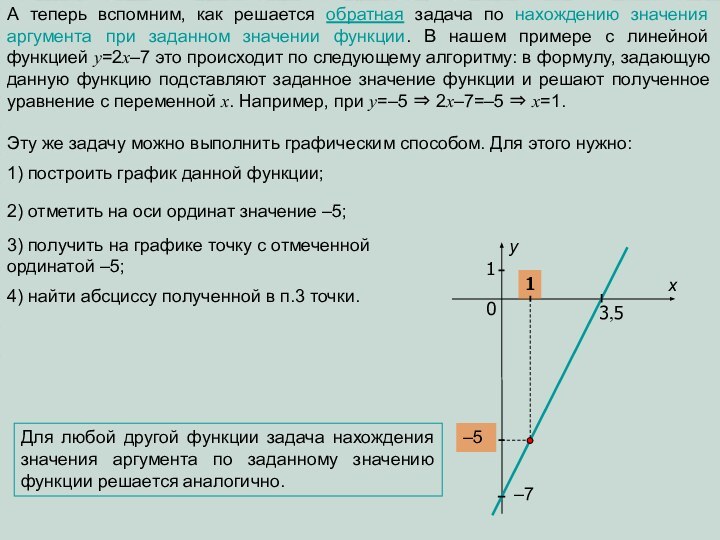
Эту же задачу можно выполнить графическим способом. Для этого нужно:
1) построить график данной функции;

x

y

1

0

1

–7

3,5

2) отметить на оси абсцисс значение 2;

–3

2

3) получить на графике точку с отмеченной абсциссой 2;

4) найти ординату полученной в п.3 точки.

Для любой другой функции задача нахождения значения функции по заданному значению аргумента решается аналогично.

нахождению значения аргумента при заданном значении функции. В нашем

Эту же задачу можно выполнить графическим способом. Для этого нужно:
1) построить график данной функции;

2) отметить на оси ординат значение –5;

3) получить на графике точку с отмеченной ординатой –5;

4) найти абсциссу полученной в п.3 точки.

x

1

0

1

–7

3,5

–5

Для любой другой функции задача нахождения значения аргумента по заданному значению функции решается аналогично.

y

1

Для этого составляют обратную зависимость, считая заданное значение данной

Выразить из формулы данной функции х через у. В нашем случае:
y=2x–7  2х=у+7  х=0,5у+3,5. А теперь записать эту зависимость, как новую функцию, в привычном для нас виде: у=0,5х+3,5. Или

2) Поменять в формуле данной функции х и у. В нашем случае:
y=2x–7  х=2у–7. А теперь записать эту зависимость, как новую функцию, в привычном для нас виде, выразив у через х : 2у=х+7  у=0,5х+3,5.

умножить на 2 и вычесть 7

D(y) - область определения.

E(y) - область значений.

y=2x–7

прибавить 7 и разделить на 2.

D(y) - область определения

E(y) - область значений

зависимость, которая является в свою очередь также функцией у=0,5х+3,5.

Примечание 1. Если для данной функции можно составить обратную зависимость, являющуюся также функцией, то говорят , что данная функция обратима и обратная зависимость является обратной функцией.

Примечание 2. Если функция y=f(x) является обратимой и y=g(x) – обратная для неё функция, то:
1) D(f)=E(g) и E(f)=D(g); 2) f(g(х))=g(f(х))=x.

Примечание 3. Графики данной и обратной для неё функций симметричны относительно прямой у=х.

обратные функции.
1
0
1
x
y
f(x)=2x–7
g(x)=0,5x+3,5
y=x

функцией необходимо и достаточно, чтобы каждое свое значение функция

1

0

1

x

y

y=x

3

–3

9

D(y)

E(y)

D(y)

E(y)

данная функция обратимой на своей области определения? 2) на

y=x

Так как эта функция является монотонной, в зависимости от

Теперь перед нами встает проблема выражения из последнего равенства переменной y (показателя степени, в который возводится положительное число a) через x, чтобы получить привычную формулу зависимости. Это делается с помощью нового понятия – логарифма числа по основанию a:

Читают так: «логарифм икс по основанию а».

Определение. Логарифмом числа x по основанию a называется показатель степени, в которую нужно возвести основание a, чтобы получить число x.

Число a называется основанием логарифма, число x называют подлогарифмическим выражением.

a>0, a1, то основание логарифма обладает такими же свойствами.
Примечание

А теперь постарайтесь ответить на вопрос: в какую степень нужно возвести число 3, чтобы результатом этой степени получилось число 10?

3 = 10

?

функций:
Используя данные рисунки сформулируйте и запишите свойства логарифмической функции.