построить, зная свойства основных элементарных функций вида y=f
(x).гипотеза
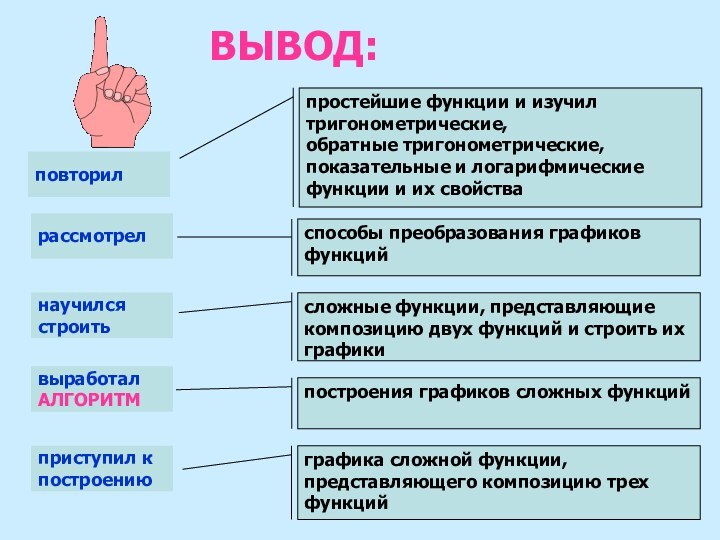
Выработаем
простой алгоритм построения графиков.
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Построение графиков функций сложных функций на основе свойств монотонности
Содержание
- 2. Графики сложных функций вида y=f (v (x))
- 3. 1. Область определения/ область значения функций2. Четность/нечетность функций3. Монотонность функцийосновные свойства функцийДЛЯ ЭТОГО ВСПОМНИМ
- 4. Симметричное отображениеПараллельный переносРастяжениеСжатиеи преобразования графиков
- 5. к построениюП Р И С Т У П И Мграфиков сложных функцийвида y=f (v (x)).
- 6. Сложная функция (четная). xvvxyy000111110,5-1-11V=1+х2Y=1/VКонтрольные точки: (1;0,5), (-1;0,5).-1-1
- 7. Сложная функция y=arctg 2x xvvxyy000111∏/2-11V= 2xY=arctg VКонтрольные точки: (0;∏/4).∏/2-1-∏/2∏/41/2-1
- 8. Сложная функция y=arctg 1/x, х=0 xvvxyy000111∏/2√3-1-11V=1/XY=arctg VКонтрольные точки: (1;∏/4), (√3;∏/6).∏/2-1-∏/2-∏/2∏/4- ∏/4∏/6
- 9. Таким образом я построил графики сложных функций:xxy00011∏/2-11Y=2
- 10. 1. начертить графики внутренней
- 11. 00131-111/2232-1x1Y= 2vyy1/2v, где х=1, х=3 0x1231u0vU=x2-4x+3-1xV=1/(x2-4x+3)123
- 12. Скачать презентацию
- 13. Похожие презентации
Графики сложных функций вида y=f (v (x)) легко построить, зная свойства основных элементарных функций вида y=f (x).гипотезаВыработаемпростой алгоритм построения графиков.
Слайд 2 Графики сложных функций вида y=f (v (x)) легко
Слайд 3
1. Область определения/
область значения функций
2. Четность/нечетность
функций
3. Монотонность функций
основные
свойства функций
ДЛЯ ЭТОГО ВСПОМНИМ
Слайд 6 Сложная функция
(четная).
x
v
v
x
y
y
0
0
0
1
1
1
1
1
0,5
-1
-1
1
V=1+х2
Y=1/V
Контрольные точки: (1;0,5), (-1;0,5).
-1
-1
Слайд 7
Сложная функция y=arctg 2x
x
v
v
x
y
y
0
0
0
1
1
1
∏/2
-1
1
V= 2x
Y=arctg V
Контрольные точки:
(0;∏/4).
∏/2
-1
-∏/2
∏/4
1/2
-1
Слайд 8
Сложная функция y=arctg 1/x, х=0
x
v
v
x
y
y
0
0
0
1
1
1
∏/2
√3
-1
-1
1
V=1/X
Y=arctg V
Контрольные точки:
(1;∏/4), (√3;∏/6).
∏/2
-1
-∏/2
-∏/2
∏/4
- ∏/4
∏/6
Слайд 9
Таким образом я построил графики сложных функций:
x
x
y
0
0
0
1
1
∏/2
-1
1
Y=2 1/х
Y=arctg
lnх
1/2
-1
-∏/2
∏/2
∏/4
- ∏/2
3∏/2
y
x
2
1/2
-3
3
3
Y=ln (x2-3х+2)
x
y
0
1
-1
2/∏
- 4/∏
Y=1/arctg х,
D (y)=(-∞;0) U (0;+∞)
y
y
2
1
0
x
Y=
2 sinх Слайд 10 1. начертить графики внутренней v
= v(x) и внешней
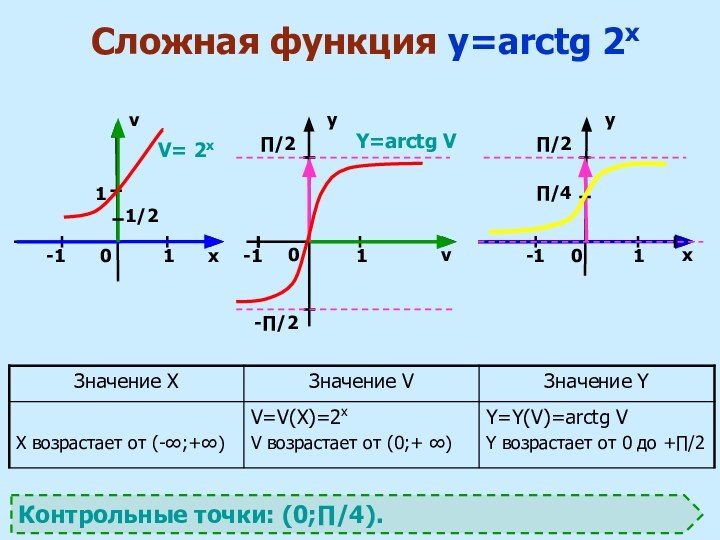
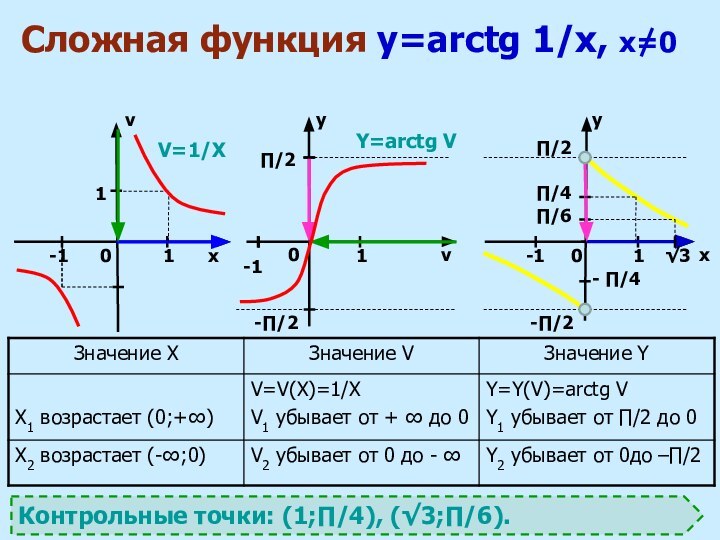
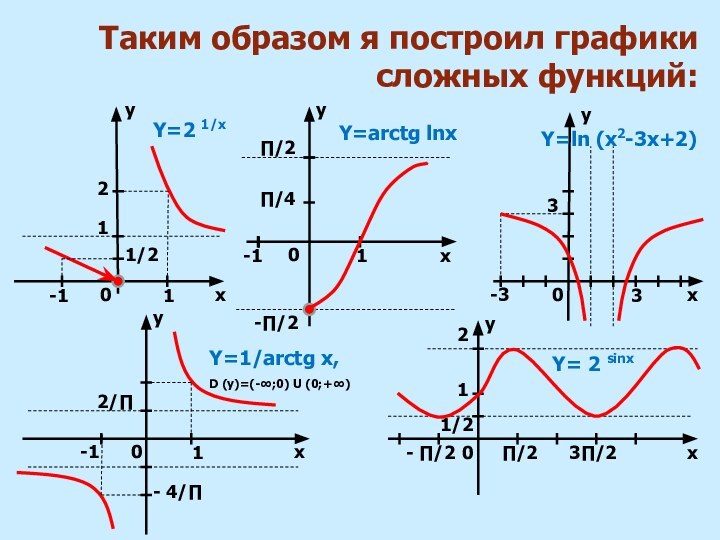
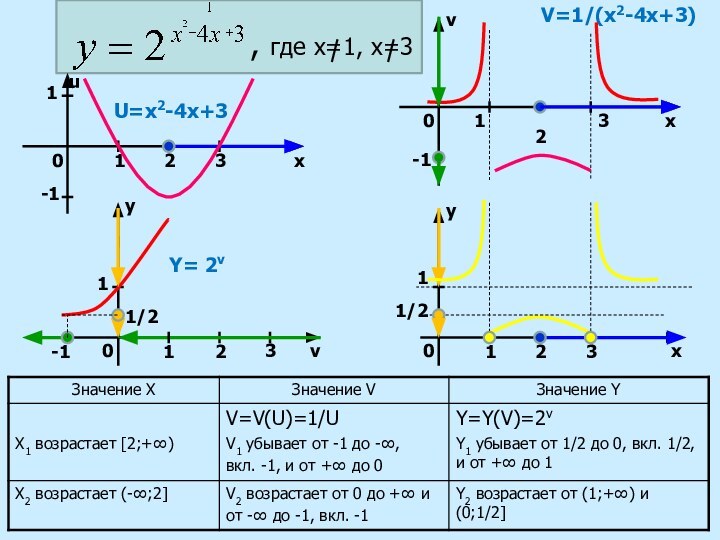
y = f (v) функций и систему координат XOY. 6. построить график сложной функции y = y (x) в системе координат XOY с учетом промежутков монотонности Х, Y и контрольных точек.
2. определить промежутки монотонности внутренней функции v = v (x).
4. на каждом промежутке определить границы изменения функции v = v(x) и выбрать те значения v (x), которые попадают в область определения функции y = f (v).
3. определить промежутки монотонности внешней функции y = f(v).
5. по графику внешней функции y = f (v) найти характер изменения функции y.
Алгоритм
построения
графиков сложных функций
И ВЫРАБОТАЛ
АЛГОРИТМ
