- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Правильные многогранники
Содержание
- 2. Правильные многогранники– это выпуклый многогранник, у которого
- 3. Полуправильные многогранники– это выпуклый многогранник, гранями которого
- 5. Попытка классификации многогранников привела в
- 6. — это правильный невыпуклый многогранник. Они получаются
- 7. Применение компьютерной программы"Математика" При помощи компьютерной
- 8. Кроме этого компьютерная программа позволят получать каркасные
- 9. Решим задачу по получению звезды Кеплера. Этот
- 10. Скачать презентацию
- 11. Похожие презентации








Слайд 2
Правильные многогранники
– это выпуклый многогранник, у которого гранями
являются правильные многоугольники и все многогранные углы равны.
Слайд 3
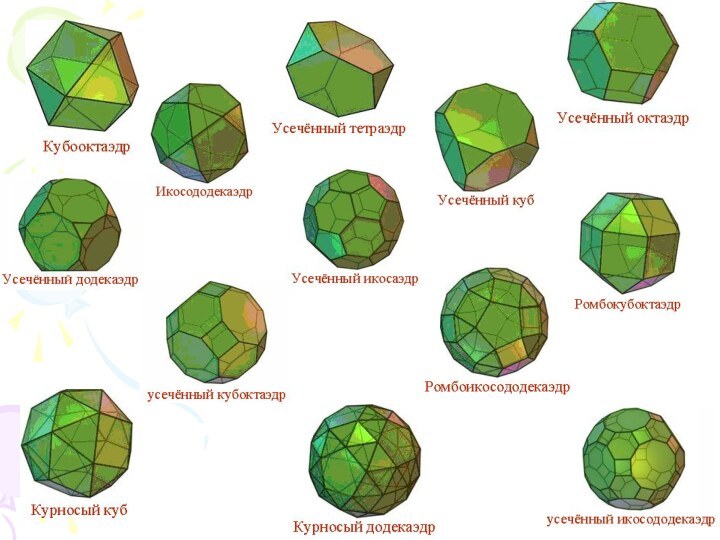
Полуправильные многогранники
– это выпуклый многогранник, гранями которого является
правильные многоугольники (возможно, с разным числом сторон) и все
многогранные углы раны.К полуправильным многогранникам относятся правильные
n-угольные призмы, все ребра которых равны, а также так называемые антипризмы. Кроме этих двух бесконечных серий полуправильных многогранников имеется еще 13 полуправильных многогранников, которые впервые открыл и описал Архимед, - это тела Архимеда
Слайд 5 Попытка классификации многогранников привела в 1750
году известнейшего математика Леонарда Эйлера к следующему результату.
В - Р + Г = 2 Где В – число вершин, Р – число ребер,
Г – число граней многогранника.
Теорема Эйлера
Проверим теорему Эйлера на полуправильных многогранниках. В – Р + Г = 2
Кубооктаэдр: 12 – 24 + 14 = 2 ПОДХОДИТ
Икосододекаэдр: 30 – 60 + 32 = 2 ПОДХОДИТ
Курносый додекаэдр: 60-150+92=2 ПОДХОДИТ
Вывод: Теорема Эйлера выполняется и для полуправильных многогранников.
Слайд 6 — это правильный невыпуклый многогранник. Они получаются из
правильных многогранников продолжением их граней или рёбер.
Звездчатые многогранники
Слайд 7
Применение компьютерной программы
"Математика"
При помощи компьютерной программы
мы можем изображать правильные многогранники и получать из них
полуправильные. Для этого нужно набрать< и мы получим додекаэдр. Если вместо Dodecahedron написать соответственно Tetrahedron, Octahedron, Hexahedron, Icosahedron, то получим изображения тетраэдра, октаэдра, куба и икосаэдра. В программе «Математика» имеется операция «Truncate», при которой от правильных многогранников отсекаются углы и в результате получаются полуправильные многогранники. Так, например, использование команды <
Show [p, Boxed->False]
Show [Truncate[p], Boxed->False]
Приводит к усеченному додекаэдру.
Слайд 8 Кроме этого компьютерная программа позволят получать каркасные изображения
любого из выбранных вами многогранников.
Каркасное изображение тетраэдра.
Каркасное изображение
икосаэдра.
Слайд 9
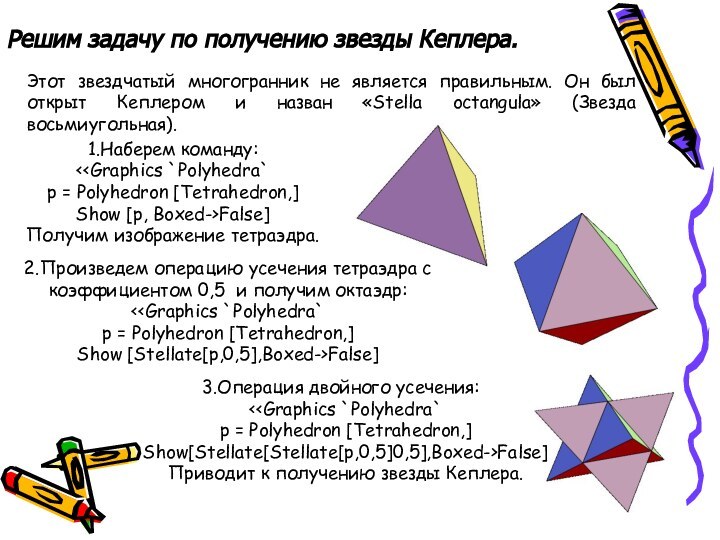
Решим задачу по получению звезды Кеплера.
Этот звездчатый
многогранник не является правильным. Он был открыт Кеплером и
назван «Stella octangula» (Звезда восьмиугольная).1.Наберем команду: 2.Произведем операцию усечения тетраэдра с коэффициентом 0,5 и получим октаэдр: 3.Операция двойного усечения:
<
Show [p, Boxed->False]
Получим изображение тетраэдра.
<
Show [Stellate[p,0,5],Boxed->False]
<
Show[Stellate[Stellate[p,0,5]0,5],Boxed->False]
Приводит к получению звезды Кеплера.





























