- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Правильные многогранники. Симметрия
Содержание
- 2. Правильный многогранник - это выпуклый
- 3. МногогранникВыпуклыйНевыпуклый
- 4. Грани многогранника - это многоугольники, которые
- 5. Тетраэдр - простейший многогранник, гранями которого являются
- 6. Куб (гексаэдр).Куб (гексаэдр) - правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.
- 7. Октаэдр.Октаэдр - выпуклый правильный многогранник.Октаэдр имеет 8 треугольных
- 8. Икосаэдр.Икосаэдр - правильный выпуклый многогранник.Каждая из 20
- 9. Додекаэдр.Додекаэдр – правильный многогранник. Каждая вершина додекаэдра
- 10. Многогранник называется правильным, если: он выпуклый; все
- 11. Симметрия в пространстве. Точки А и
- 12. Симметрия в архитектуре.
- 13. Симметрия в природе.
- 14. Симметрия в технике.
- 15. Симметрия в быту.
- 16. Скачать презентацию
- 17. Похожие презентации
Правильный многогранник - это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.Существует 5 видов правильных многогранников:















Слайд 2 Правильный многогранник - это выпуклый многогранник,
состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.
5 видов правильных многогранников:Слайд 4 Грани многогранника - это многоугольники, которые его
образуют.
Ребра многогранника - это стороны многоугольников.
Вершины
многогранника - это вершины многоугольника.Диагональ многогранника - это отрезок, соединяющий 2 вершины, не принадлежащие одной грани.
Элементы многогранника.
Слайд 5 Тетраэдр - простейший многогранник, гранями которого являются четыре
треугольника.
У тетраэдра 4 грани, 4 вершины и 6
рёбер.Тетраэдр.
Слайд 6
Куб (гексаэдр).
Куб (гексаэдр) - правильный многогранник, каждая грань которого
представляет собой квадрат. Частный случай параллелепипеда и призмы.
Слайд 7
Октаэдр.
Октаэдр - выпуклый правильный многогранник.
Октаэдр имеет 8 треугольных граней,
12 рёбер,
6 вершин, в каждой его вершине сходятся
4 ребра.
Слайд 8
Икосаэдр.
Икосаэдр - правильный выпуклый многогранник.
Каждая из 20 граней
представляет собой равносторонний треугольник.
Число рёбер равно 30, число
вершин - 12.
Слайд 9
Додекаэдр.
Додекаэдр – правильный многогранник.
Каждая вершина додекаэдра является
вершиной трёх правильных пятиугольников.
Додекаэдр имеет 12 граней (пятиугольных), 30
рёбер и 20 вершин (в каждой сходятся 3 ребра).
Слайд 10
Многогранник называется правильным, если:
он выпуклый;
все его
грани являются равными правильными многоугольниками;
в каждой его вершине
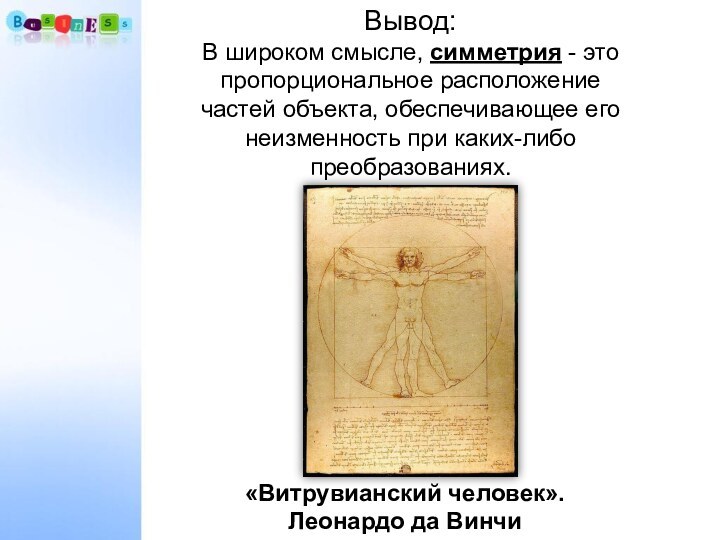
сходится одинаковое число рёбер.Вывод.
Слайд 11
Симметрия в пространстве.
Точки А и А1
называются симметричными относительно точки О (центр симметрии), если О
– середина отрезка АА1.Точка О считается симметричной самой по себе.
Точки А и А1 называются симметричными относительно прямой а (ось симметрии), если прямая а проходит через середину отрезка АА1 и перпендикулярна к этому отрезку.
Каждая точка прямой а считается симметричной самой себе.
Точки А и А1 называются симметричными относительно плоскости α (плоскость симметрии), если плоскость α проходит через середину отрезка АА1 и перпендикулярна к этому отрезку. Каждая точка плоскости α считается симметричной самой себе.