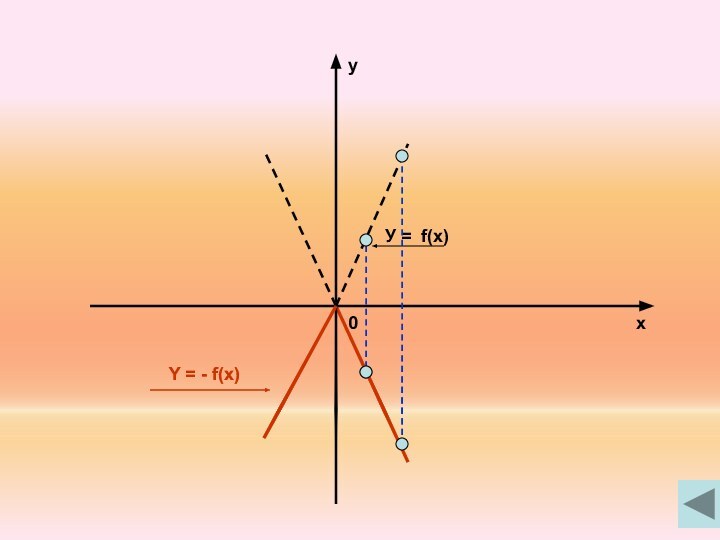
f(x) ← y = f(x) , отображением относительно оси
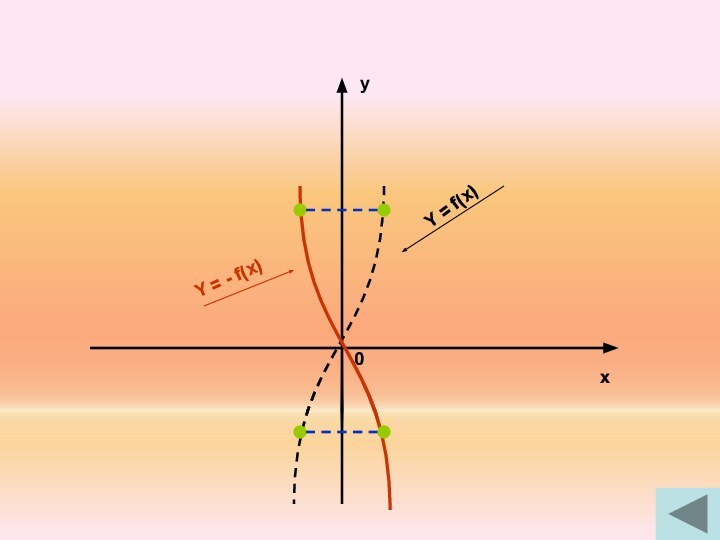
ОХ.2. У = f(- x) ← y = f(x), отображением от оси ОУ.
3. У = - f (- x) ← y = f(x), отображением относительно начала координат.
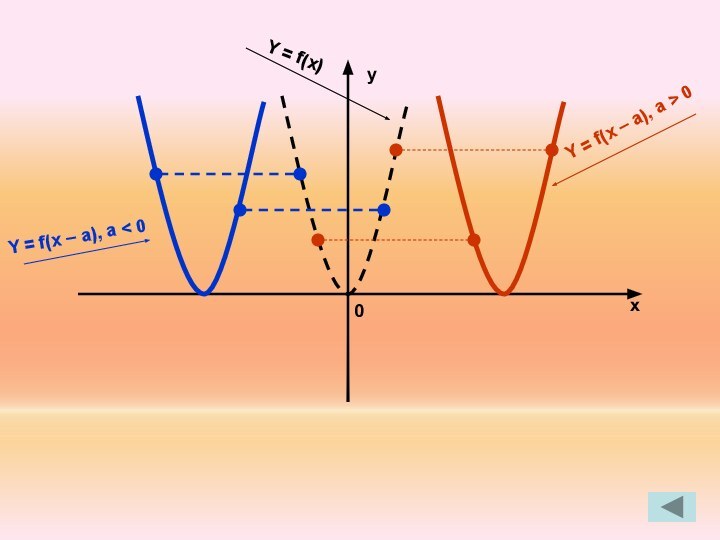
4. У = f(x – a) ← y = f(x),параллельным переносом вправо по ОХ, если а >0,
влево по ОХ, если а < 0.
5. У = f(x) + b ← y = f(x), параллельным переносом вверх по ОУ, если в > 0,
вниз по ОУ, если в < 0.
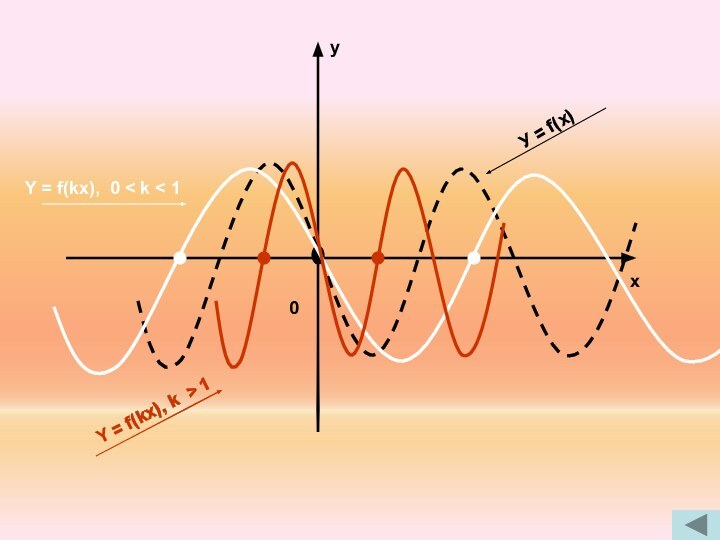
6. У = f(kx) ← y = f(x), растяжением в вдоль оси ОХ в 1/к раз, если 0 < к < 1;
сжатием вдоль оси ОХ в к раз, если к > 1.
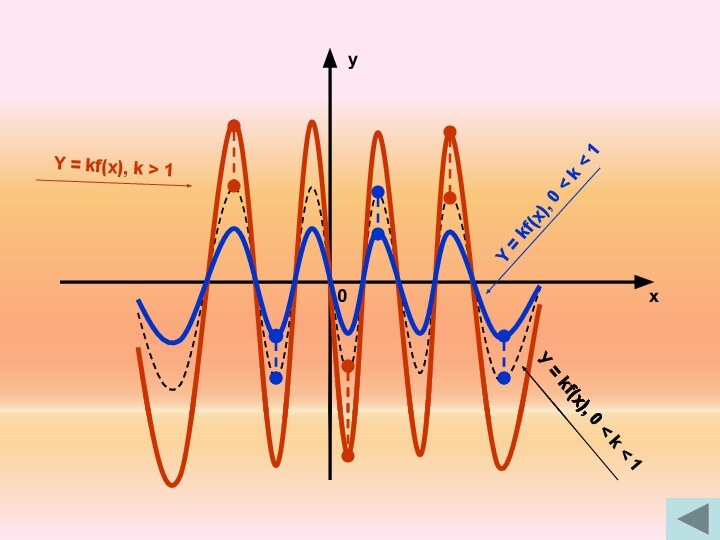
7. У = kf(x) ← y = f(x), сжатием вдоль оси ОУ в 1/к раз, если 0 < к < 1 и
растяжением вдоль оси ОУ в к раз, если к > 1.
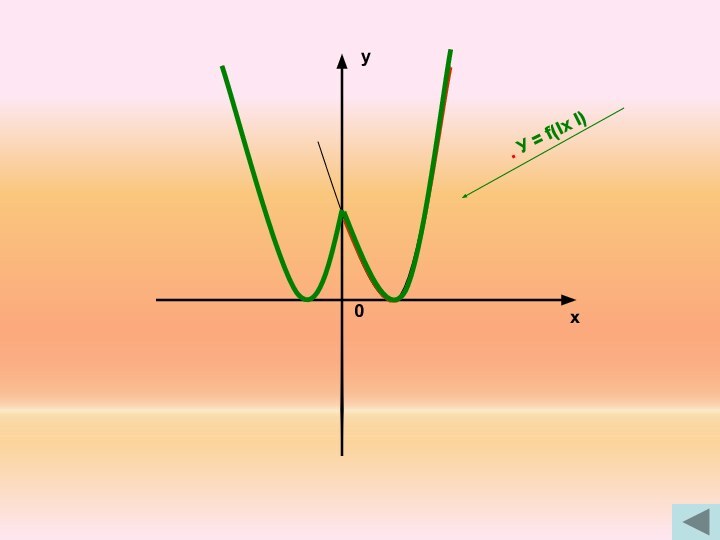
9. У = f(Ix I) ← y = f(x) строим график функции y = f(x) при х ≥ 0 и
отображением его относительно оси ОУ.
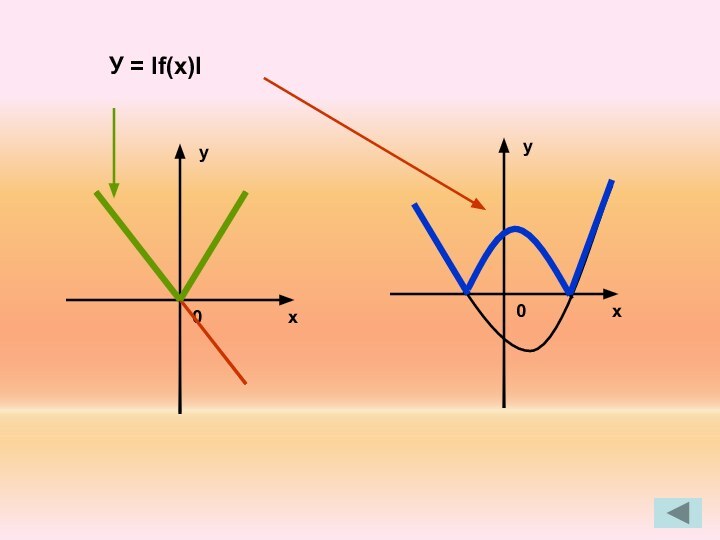
8. У = If(x)I – совпадает с у = f(x) в тех точках, которые лежат выше оси ОХ
симметричен графику у = f(x) относительно оси абсцисс в остальных точках.