- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение заданий части С по алгебре
Содержание
- 2. Решение заданий части С по алгебре
- 3. Задание С1 в КИМах ЕГЭ интересно тем,
- 4. а). Решите уравнениеб). Найдите все корни этого
- 5. Найдите все корни этого уравнения, принадлежащие отрезку n=-1n=-1
- 6. xб). Найдите все корни этого уравнения, принадлежащие отрезку Отбор корней с помощью графиков
- 7. -3πВыбрать корни по тригонометрическому кругу удобно, т.к.
- 8. Эксперты оценивают выполнение задания по следующим
- 9. а). Решите уравнениеб). Найдите все корни этого
- 10. б). Найдите все корни этого уравнения, принадлежащие отрезку Отбор корней с помощью решения неравенствn=0
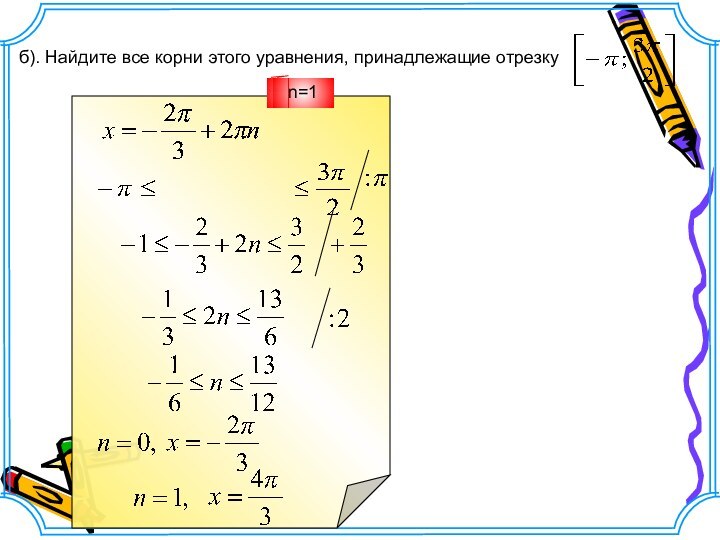
- 11. б). Найдите все корни этого уравнения, принадлежащие отрезку n=0n=1
- 12. б). Найдите все корни этого уравнения, принадлежащие отрезку n=0
- 13. yx1-1б). Найдите все корни этого уравнения, принадлежащие отрезку Отбор корней с помощью графиков
- 14. yx1-1б). Найдите все корни этого уравнения, принадлежащие отрезку Отбор корней с помощью графиков
- 15. π0Выбирать корни по тригонометрическому кругу не удобно,
- 16. π0б). Найдите все корни этого уравнения, принадлежащие
- 17. Третье задание части С из экзамена ЕГЭ
- 19. Пример1: (1 способ)
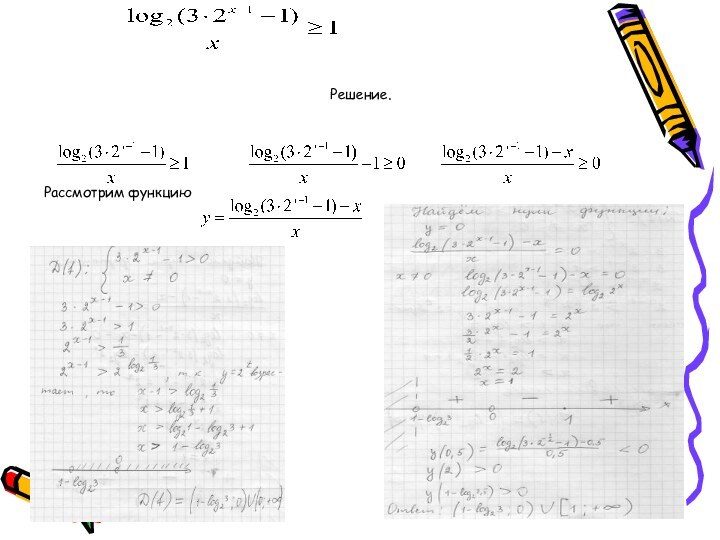
- 21. Решение.Рассмотрим функцию
- 22. Основные ошибки при решении неравенств (С3) Ошибки
- 23. Алгоритм решения задач с параметром графическим методом1.
- 24. Найдите все значения р, при каждом из
- 25. Найти все значения параметра `a`, при каждом
- 26. Для успешного решения задач типа С5 необходимо:
- 27. Источники:1. http://alexlarin.narod.ru 2. http://www.akipkro.ru/ 3. http://4ege.ru/matematika/4. http://www.ctege.info/content/5.
- 28. Скачать презентацию
- 29. Похожие презентации

















Слайд 4
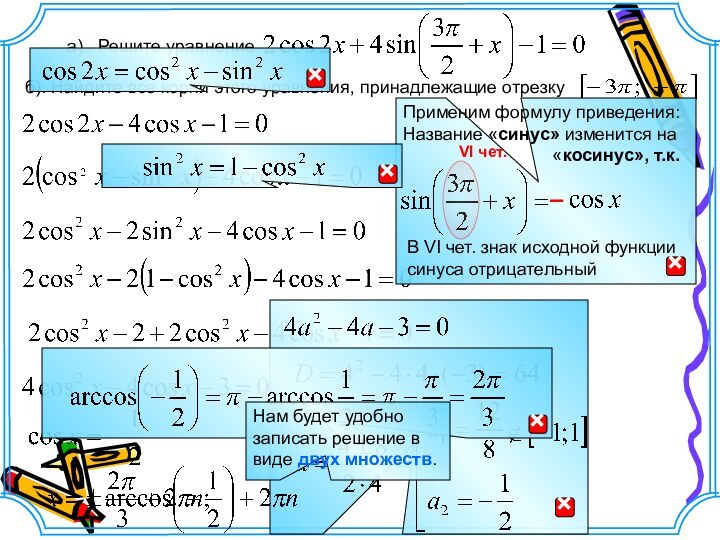
а). Решите уравнение
б). Найдите все корни этого уравнения,
принадлежащие отрезку
VI чет.
В VI чет. знак исходной функции
синуса отрицательный
–
Нам будет удобно записать решение в виде двух множеств.
Слайд 6
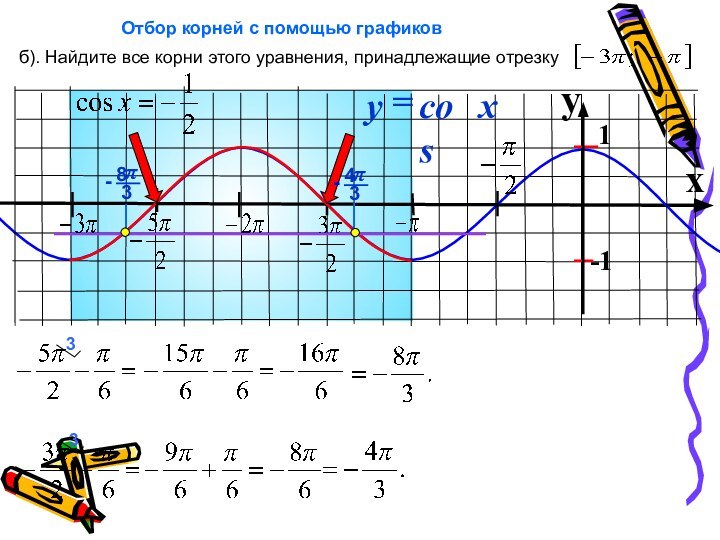
x
б). Найдите все корни этого уравнения, принадлежащие отрезку
Отбор корней с помощью графиков
Слайд 7
-3π
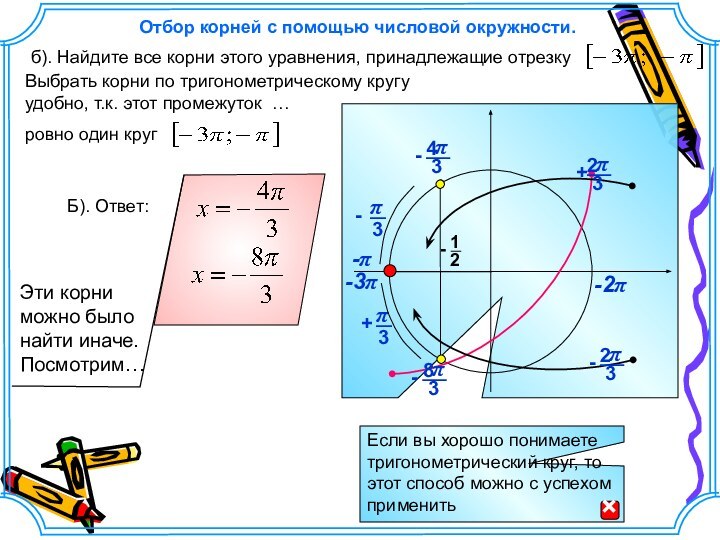
Выбрать корни по тригонометрическому кругу удобно, т.к. этот
промежуток …
ровно один круг
б). Найдите все корни
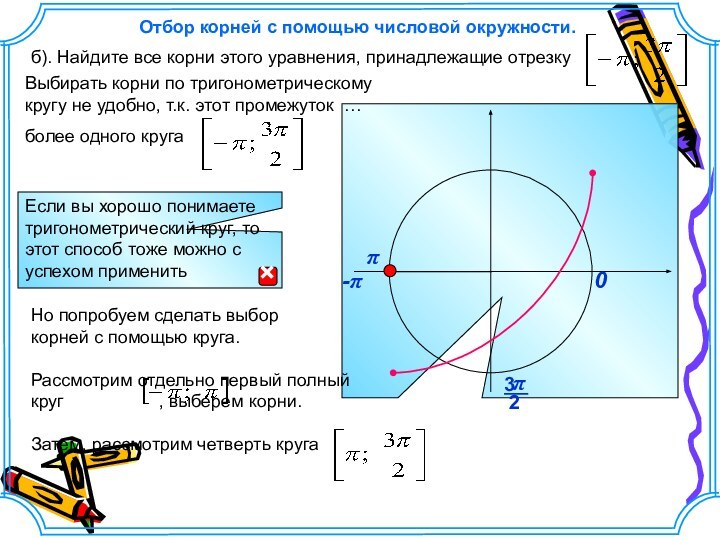
этого уравнения, принадлежащие отрезку Отбор корней с помощью числовой окружности.
-2π
-π
Б). Ответ:
Слайд 8 Эксперты оценивают выполнение задания по следующим критериям. -
Обоснованно получены ответы в обоих пунктах - 2 балла,
это максимальный балл. - Обоснованно получен ответ в пункте а или в пункте б - 1 балл. - Решение не соответствует ни одному из критериев, перечисленных выше - 0 баллов.
Слайд 9
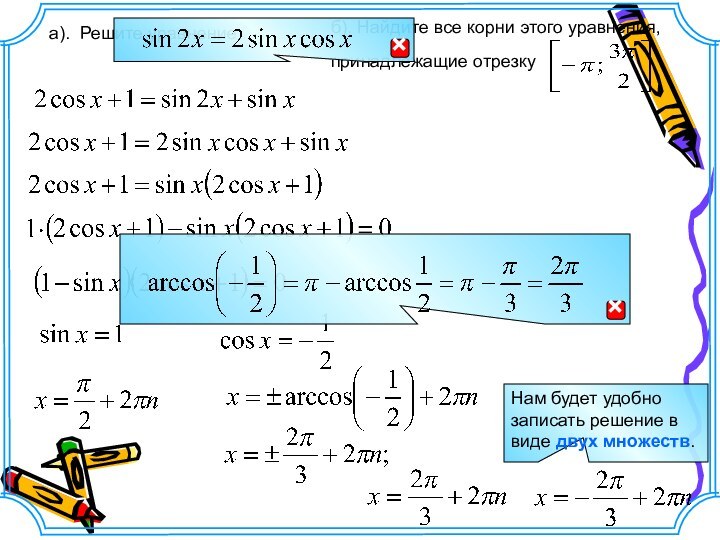
а). Решите уравнение
б). Найдите все корни этого уравнения,
принадлежащие отрезку
Нам будет удобно записать решение в виде
двух множеств.
Слайд 10
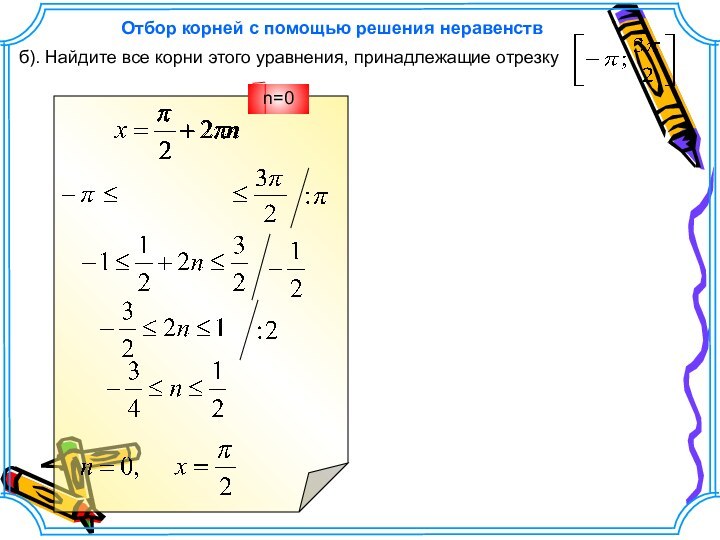
б). Найдите все корни этого уравнения, принадлежащие отрезку
Отбор корней с помощью решения неравенств
n=0
Слайд 13
y
x
1
-1
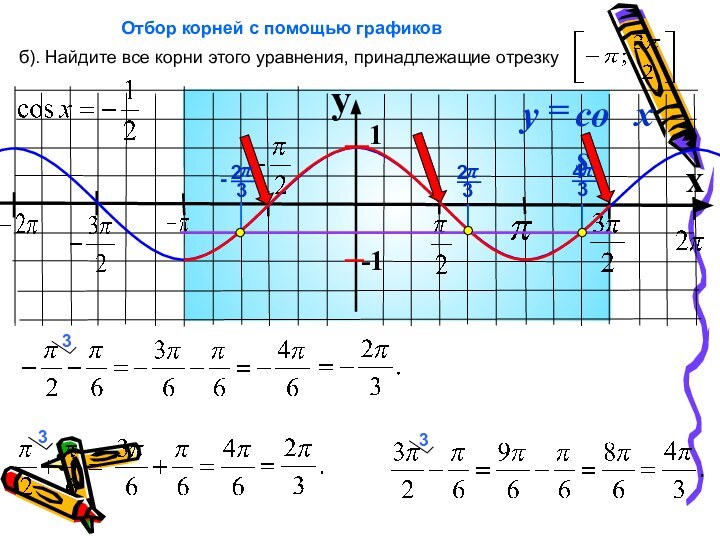
б). Найдите все корни этого уравнения, принадлежащие отрезку
Отбор корней с помощью графиков
Слайд 14
y
x
1
-1
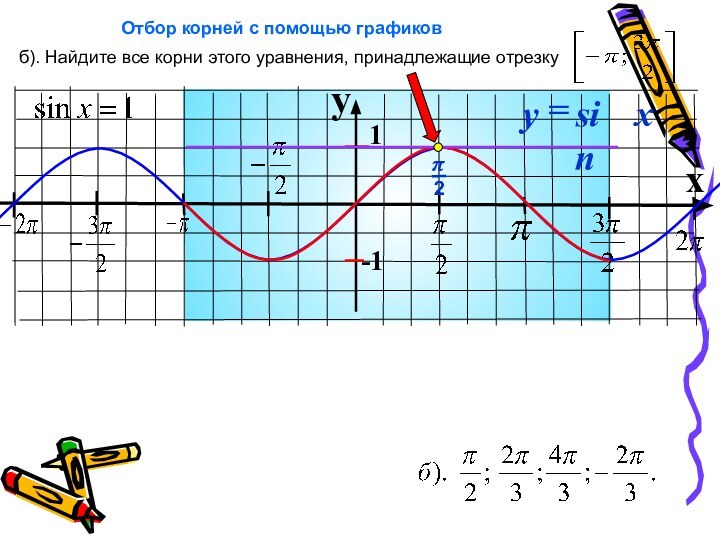
б). Найдите все корни этого уравнения, принадлежащие отрезку
Отбор корней с помощью графиков
Слайд 15
π
0
Выбирать корни по тригонометрическому кругу не удобно, т.к.
этот промежуток …
более одного круга
б). Найдите все
корни этого уравнения, принадлежащие отрезку Но попробуем сделать выбор корней с помощью круга.
Рассмотрим отдельно первый полный круг , выберем корни.
Затем, рассмотрим четверть круга
Отбор корней с помощью числовой окружности.
Слайд 16
π
0
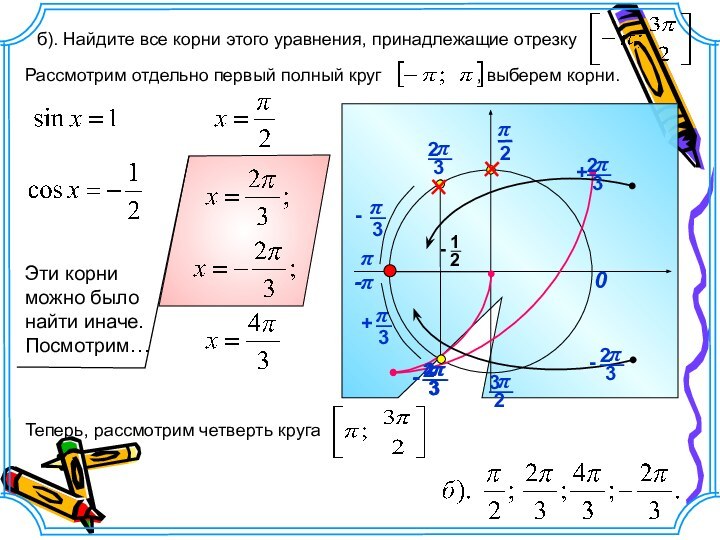
б). Найдите все корни этого уравнения, принадлежащие отрезку
Рассмотрим отдельно первый полный круг
, выберем корни. -π
Слайд 17
Третье задание части С
из экзамена ЕГЭ
по
математике посвящена
решению системы неравенств.
Третье задание части С
из экзамена ЕГЭ
по математике посвящена
решению системы неравенств.
Слайд 22
Основные ошибки при решении неравенств (С3)
Ошибки в
применении свойств логарифма.
Плохое знание свойств логарифмической функции, показательной.
Неумение применять
замену переменной.Неумение применять метод интервалов при решении неравенств повышенного и высокого уровней сложности.
Неумение применять метод равносильных преобразований, при решении неравенств повышенного и высокого уровней сложности.
Некорректное использование систем и совокупностей.
Незнание рациональных методов решения неравенств повышенного и высокого уровня сложности.
Слайд 23
Алгоритм решения задач с параметром графическим методом
1. Преобразовываем
исходное условие задачи к системе неравенств, в которых неизвестное
выражается через параметр, или, наоборот, параметр выражается через неизвестное.2. Вводим систему координат (а;х), если мы неизвестное выражали через параметр, или (х;а) , если, наоборот, параметр выражали через неизвестное.
3. Изображаем в выбранной координатной плоскости фигуру, которая задается множеством решений системы неравенств.
4. «Сканируем» эту фигуру, двигаясь вдоль оси параметра и определяем, при каких значениях параметра выполняются заданные в задаче условия.
5. Записываем ответ.
Слайд 24 Найдите все значения р, при каждом из которых
для любого q система
имеет решения.Решение.
График функции, заданной первым уравнением – окружность радиуса 1 с
центром в начале координат. График функции, заданной вторым уравнением
должен пересекать эту окружность при любом q, т.е. при любом угле наклона
прямых этой ломаной.
Нетрудно видеть, что это условие для любого угла наклона выполняется при сдвиге вершины ломаной по оси у не более чем на единицу вниз или вверх .
Ответ:
Слайд 25 Найти все значения параметра `a`, при каждом из
которых уравнение `ax + sqrt( -7 -8x -x^2) = 2a
+3`имеет единственное решение `ax + sqrt(-7-8x-x^2) =2a+3` перепишем как `sqrt(-7 - 8*x - x^2) = a*(-x + 2) + 3`... `y = sqrt(-7 - 8*x - x^2) ` - уравнение верхней половины окружности с центром `(-4; 0)` и радиуса `3`... `y = a*(-x + 2) + 3` - прямая, проходящая через точку `(2; 3)`... и угловым коэффициентом `k = -a`... Графики имеют одну общую точку в следующих случаях 1) касание с окружностью в точке `(-4; 3)`... при этом `a = 0`... 2) угловые коэффициенты прямых, проходящих через точки на оси икс от точки `(-7; 0)` (не включая этот случай, поскольку получаем 2 точки пересечения) до точки `(-1; 0)`... Получаем `k (3/9; 1]`... Ответ: ` [-1; -1/3) {0}`
Слайд 26
Для успешного решения задач типа С5 необходимо:
Уметь
решать уравнения и неравенства
Решать рациональные, иррациональные, показательные, тригонометрические
и логарифмические уравнения, их системы Решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков; использовать для приближенного решения уравнений и неравенств графический метод
Решать рациональные, показательные и логарифмические неравенства, их системы





























