- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Призма и ее виды
Содержание
- 2. Решётка железа Решётка магния
- 3. АквариумБашня Смоленской крепости
- 4. ОбелискБеседка
- 5. Призма
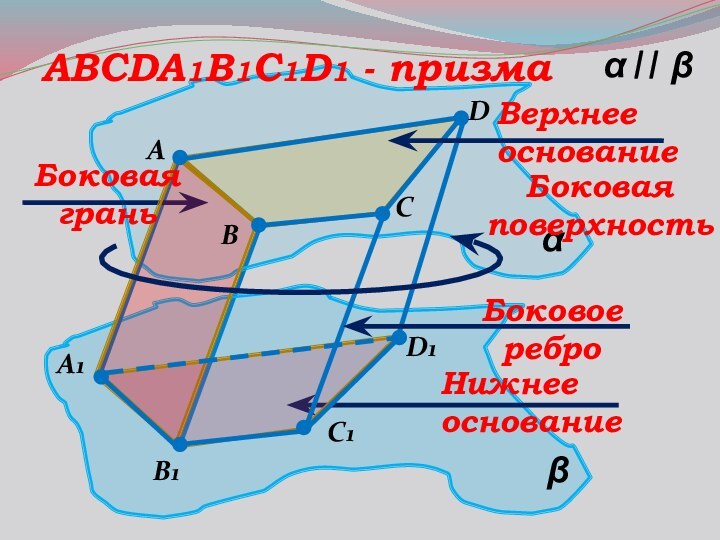
- 6. αβαβ||ABC1DA1B1D1CABCDA1B1C1D1 - призмаВерхнееоснованиеНижнееоснованиеБоковоереброБоковаяграньБоковаяповерхность
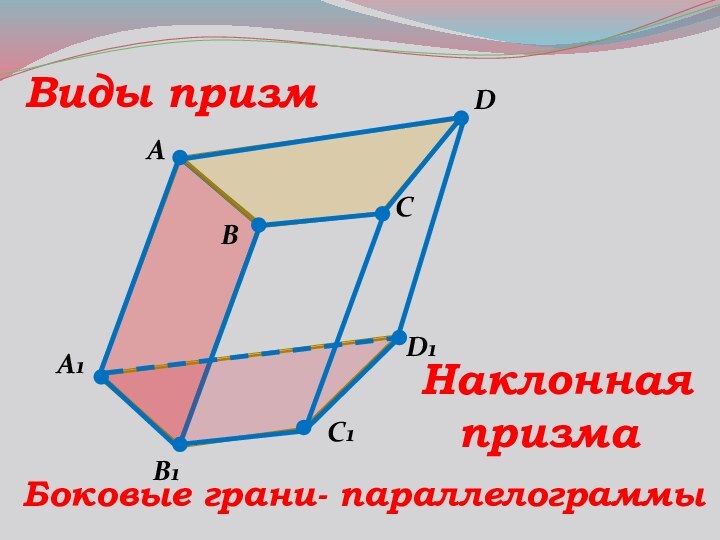
- 7. ABC1DA1B1D1CВиды призм Наклоннаяпризма Боковые грани- параллелограммы
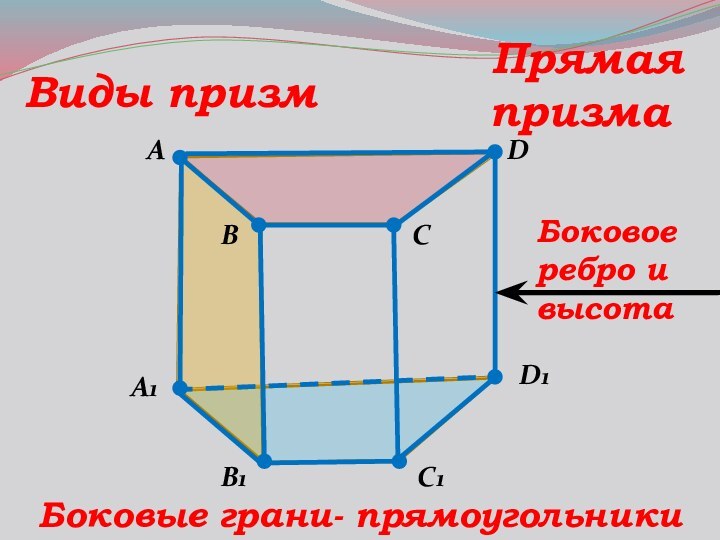
- 8. ABC1DA1B1D1CВиды призм ПрямаяпризмаБоковые грани- прямоугольникиБоковоеребро и высота
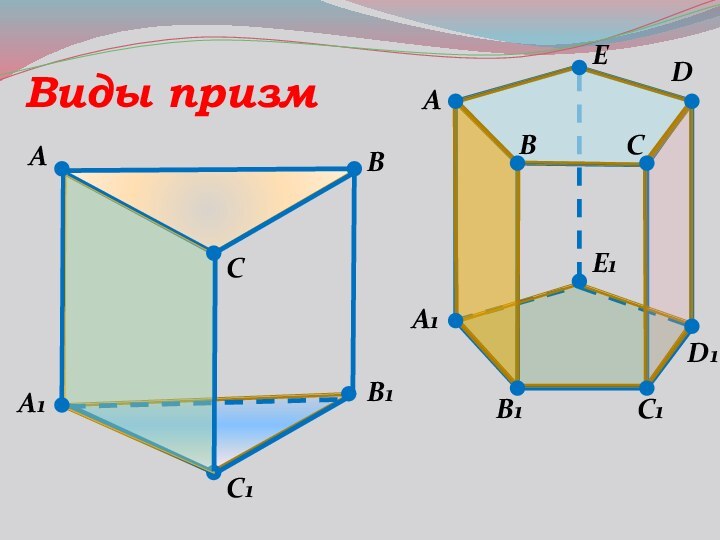
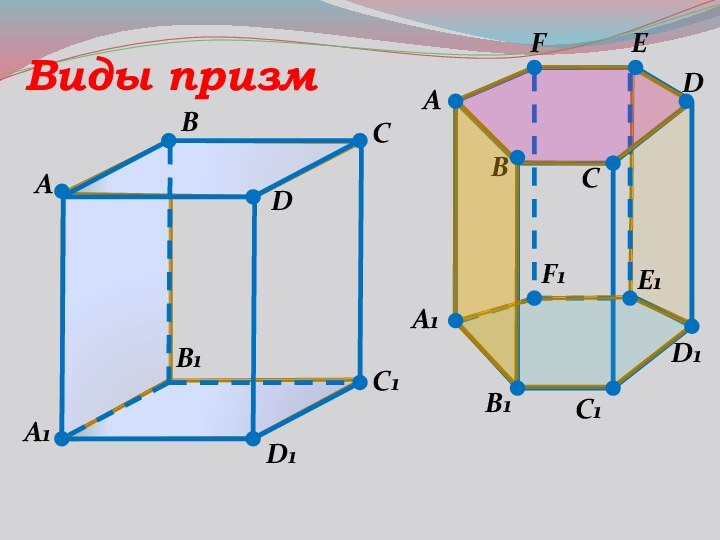
- 9. ABC1DA1B1D1CВиды призмEA1BB1CC1AE1
- 10. ABC1DA1B1D1CВиды призмEA1BB1CC1AE1DD1FF1
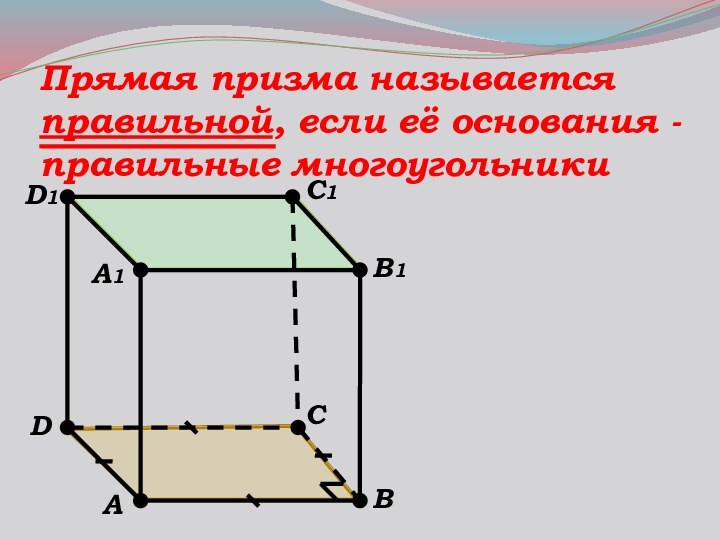
- 11. Прямая призма называется правильной, если её основания - правильные многоугольникиB1C1D1A1ABCD
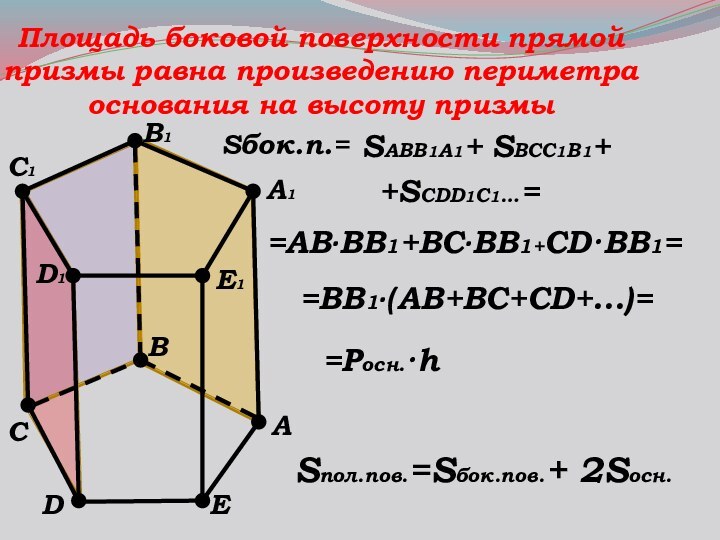
- 12. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы А1АBB1C1D1DE1ECSпол.пов.=Sбок.пов.+ 2Sосн.Sбок.п.=SАВВ1А1+ SBCC1B1+ +SCDD1C1…==АВ·ВВ1+ВС·ВВ1+CD·BB1==ВВ1·(АВ+ВС+СD+…)==Pосн.·h
- 13. Скачать презентацию
- 14. Похожие презентации
Решётка железа Решётка магния