Слайд 2
СОДЕРЖАНИЕ
1. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ
2. СПОСОБЫ ПОЛУЧЕНИЯ ГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ
3. ЦЕНТРАЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
4. ОРТОГОНАЛЬНЫЕ
ПРОЕКЦИИ И ОСНОВНЫЕ ВИДЫ ЧЕРТЕЖА
5. ПРОЕКЦИИ ТОЧКИ
6. ПРОЕКЦИИ ПРЯМОЙ
7. РАЗРЕЗЫ, СЕЧЕНИЯ И
ВИДЫ
8. РАЗМЕРЫ, ПРОСТАВЛЯЕМЫЕ НА ЧЕРТЕЖЕ ДЕТАЛИ
Слайд 3
Начертательная геометрия изучает способы построения изображений пространственных фигур
на плоскости и решения пространственных задач на чертеже.
Проекционное черчение
рассматривает практические вопросы построения чертежей и решает задачи способами, рассмотренными в начертательной геометрии, сначала на чертежах геометрических тел, а затем на чертежах моделей и технических деталей.
ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ
Слайд 4
СПОСОБЫ ПОЛУЧЕНИЯ ГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ
Форму любого предмета можно рассматривать
как сочетание отдельных простейших геометрических тел. А для изображения
геометрических тел нужно уметь изображать их отдельные элементы: вершины (точки), ребра (прямые), грани (плоскости).
В основе построения изображений лежит способ проецирования. Получить изображение какого-либо предмета — значит спроецировать его на плоскость чертежа, т.е. спроецировать отдельные его элементы. Поскольку простейшим элементом любой фигуры является точка, изучение проецирования начинают с проецирования точки.
Слайд 5
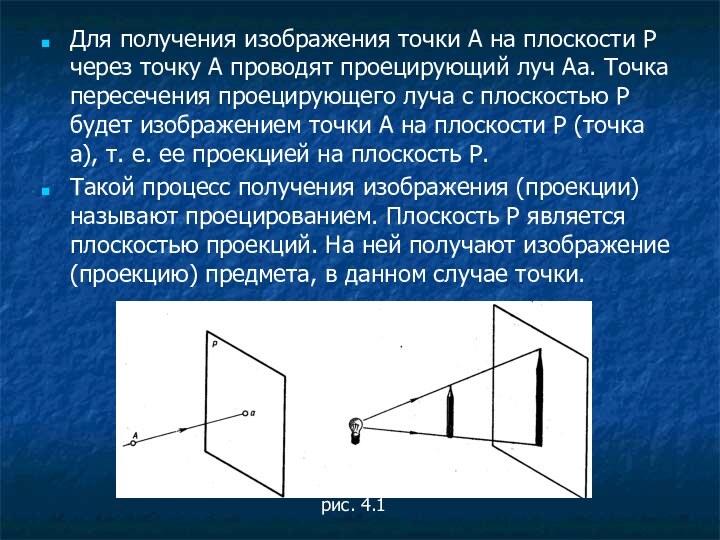
Для получения изображения точки А на плоскости Р
через точку А проводят проецирующий луч Аа. Точка пересечения
проецирующего луча с плоскостью Р будет изображением точки А на плоскости Р (точка а), т. е. ее проекцией на плоскость Р.
Такой процесс получения изображения (проекции) называют проецированием. Плоскость Р является плоскостью проекций. На ней получают изображение (проекцию) предмета, в данном случае точки.
рис. 4.1
Слайд 6
Принцип проецирования
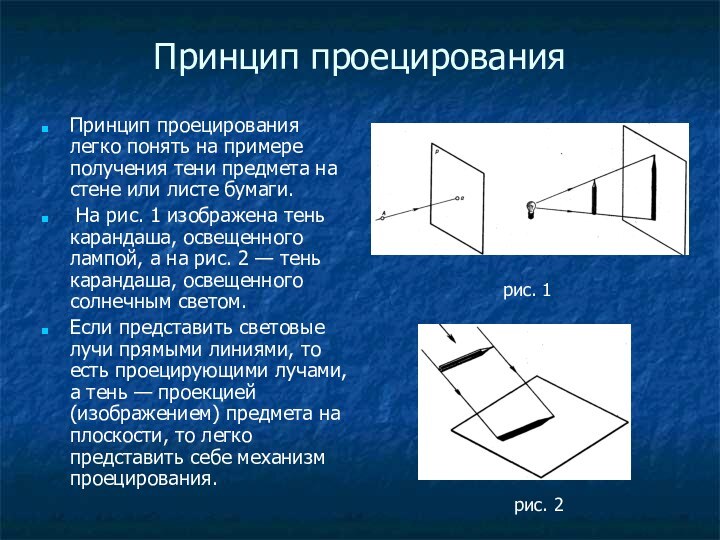
Принцип проецирования легко понять на примере получения
тени предмета на стене или листе бумаги.
На рис.
1 изображена тень карандаша, освещенного лампой, а на рис. 2 — тень карандаша, освещенного солнечным светом.
Если представить световые лучи прямыми линиями, то есть проецирующими лучами, а тень — проекцией (изображением) предмета на плоскости, то легко представить себе механизм проецирования.
рис. 1
рис. 2
Слайд 7
В зависимости от взаимного расположения проецирующих лучей проецирование
делят на центральное и параллельное.
Два вида проецирования
Слайд 8
ЦЕНТРАЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
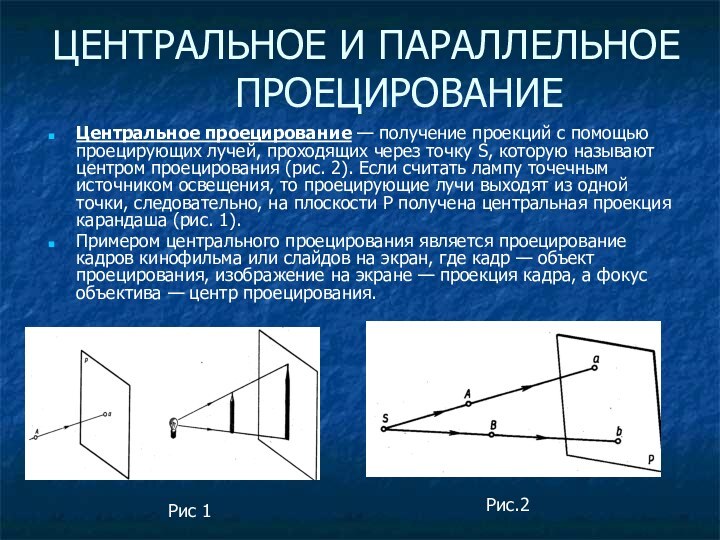
Центральное проецирование — получение проекций
с помощью проецирующих лучей, проходящих через точку S, которую
называют центром проецирования (рис. 2). Если считать лампу точечным источником освещения, то проецирующие лучи выходят из одной точки, следовательно, на плоскости Р получена центральная проекция карандаша (рис. 1).
Примером центрального проецирования является проецирование кадров кинофильма или слайдов на экран, где кадр — объект проецирования, изображение на экране — проекция кадра, а фокус объектива — центр проецирования.
Рис.2
Рис 1
Слайд 9
Изображения, получаемые способом центрального проецирования, подобны изображениям на
сетчатке нашего глаза. Они наглядны, понятны для нас, так
как показывают нам предметы окружающей действительности такими, какими мы их привыкли видеть. Но искажение размеров предметов и сложность построения изображений при центральном проецировании не позволяют использовать его для изготовления чертежей.
Центральные проекции широко применяют лишь там, где нужна наглядность в изображениях, например, в архитектурно-строительных чертежах при изображении перспектив зданий, улиц, площадей и т. п.
ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ
Слайд 10
ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
Параллельное проецирование. Если центр проецирования — точку
S удалить в бесконечность, то проецирующие лучи станут параллельными
друг другу. На рис. 1 показано получение параллельных проекций точек А и В на плоскости Р.
При прямоугольном проецировании проецирующие лучи перпендикулярны плоскости проекций (рис.2).
При косоугольном проецировании угол наклона проецирующих лучей к плоскости проекций не равен 90о (рис. 3).
Рис 1
Рис 2
Рис 3
Слайд 11
Рассмотренные выше способы проецирования не устанавливают взаимно однозначного
соответствия между объектом (точка А) и его изображением (проекцией).
При заданном направлении проецирующих лучей на плоскости проекций всегда получается лишь одна проекция точки, но судить о положении точки в пространстве по одной ее проекции невозможно, так как на одном и том же проецирующем луче Аа (рис. 4) точка может занимать различные положения, находясь выше или ниже заданной точки А, и какое положение точки в пространстве соответствует изображению (проекции) а, определить невозможно.
ы
Рис 4
ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
Слайд 12
Для того чтобы по изображению точки можно было
определить ее положение в пространстве, необходимо как минимум иметь
две проекции этой точки. При этом должно быть известно взаимное расположение плоскостей проекций и направление проецирования. Тогда, имея два изображения точки А, можно будет представить, как расположена точка в пространстве.
Наиболее простым и удобным является проецирование на взаимно перпендикулярные плоскости проекций с помощью проецирующих лучей, перпендикулярных плоскостям проекций.
Такое проецирование называют ортогональным проецированием, а полученные изображения — ортогональными проекциями.
ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ
Слайд 13
ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ И
ОСНОВНЫЕ ВИДЫ ЧЕРТЕЖА
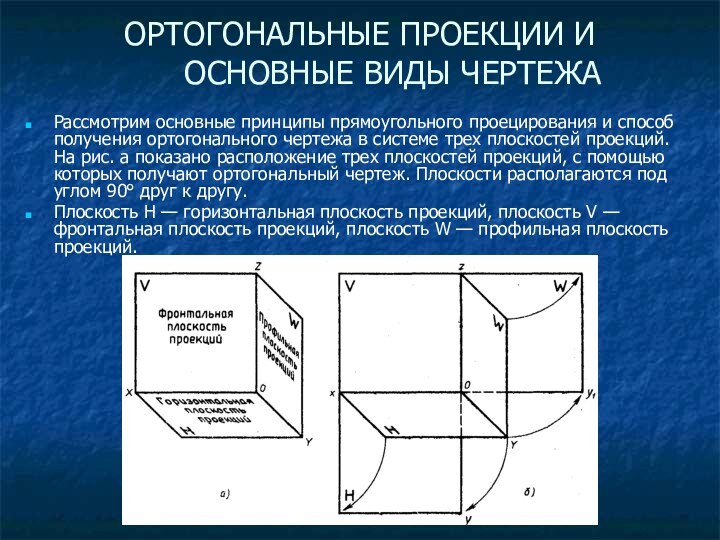
Рассмотрим основные принципы прямоугольного
проецирования и способ получения ортогонального чертежа в системе трех
плоскостей проекций. На рис. а показано расположение трех плоскостей проекций, с помощью которых получают ортогональный чертеж. Плоскости располагаются под углом 90° друг к другу.
Плоскость H — горизонтальная плоскость проекций, плоскость V — фронтальная плоскость проекций, плоскость W — профильная плоскость проекций.
Слайд 14
Линии пересечения плоскостей проекций называются осями проекций, или
осями координат и обозначаются Ox, Оу, Oz.
Точка пересечения
трех осей координат (точка О) является началом координат, т.е. точкой, от которой ведется отсчет координат по осям Ox, Qy, Oz.
Угол, образованный тремя плоскостями проекций, называют координатным у г л о м, так как плоскости проекций являются базами отсчета расстояний (координат) и ограничивают пространство плоскостями проекций, в котором располагают проецируемые предметы.
Слайд 15
Помещая изображаемый (проецируемый) предмет (геометрическая фигура, модель, деталь
и т.п.) в определенное положение относительно плоскостей проекций V.
Н и W, фиксируют его положение относительно этих плоскостей, что дает возможность получить взаимосвязанные изображения данного предмета, по которым легко представить его положение в пространстве, его форму. Каждое изображение (проекция) предмета на плоскость отображает то, что мы видим при взгляде на предмет в определенном направлении. Чтобы получить представление о форме предмета, обычно недостаточно рассмотреть предмет с какой-то одной стороны. Проецируя предмет в системе трех плоскостей проекций, его рассматривают с трех сторон, в направлениях, перпендикулярных трем плоскостям проекций.
Слайд 16
Получив проекции предмета на трех плоскостях проекций, плоскости
координатного угла развертывают в одну плоскость. При этом плоскости
H и W условно разрезают по оси Оу, плоскость H поворачивают вокруг оси Ох, а плоскость W -- вокруг оси Oz, получают одну общую плоскость — плоскость чертежа. При этом ось Оу как бы разрезаемся пополам. Одна ее «половина» оказывается в плоскости H и располагается перпендикулярно оси Ох, а другая — в плоскости W и располагается перпендикулярно оси Oz. Совмещенные плоскости проекций разделяются взаимно перпендикулярными осями, которые определяют на чертеже рабочее поле для построения проекций предмета. Каждая плоскость проекций имеет два измерения по взаимно перпендикулярным направлениям. Для плоскости Н — это оси Ох и Оу, для плоскости V — оси Oz и Оx:, для плоскости W -оси Oz и Оу.
Слайд 17
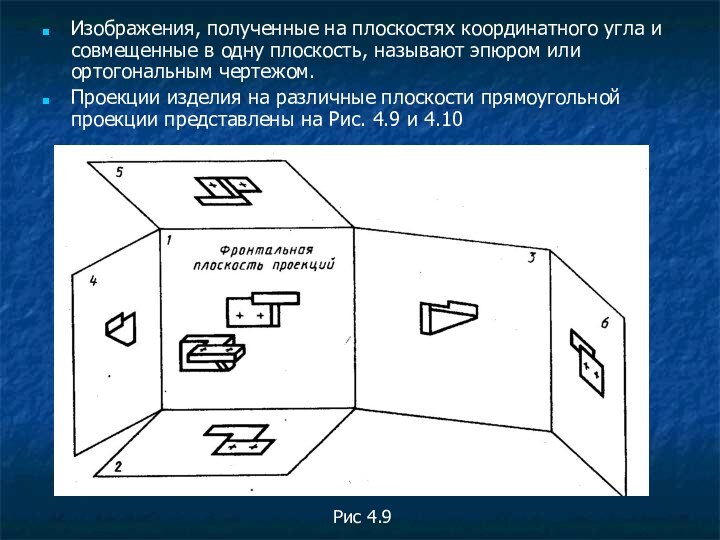
Изображения, полученные на плоскостях координатного угла и совмещенные
в одну плоскость, называют эпюром или ортогональным чертежом.
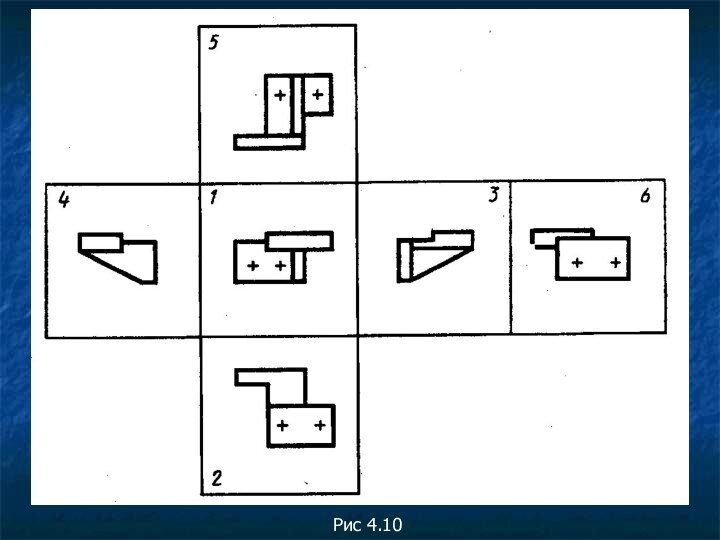
Проекции
изделия на различные плоскости прямоугольной проекции представлены на Рис. 4.9 и 4.10
Рис 4.9
Слайд 19
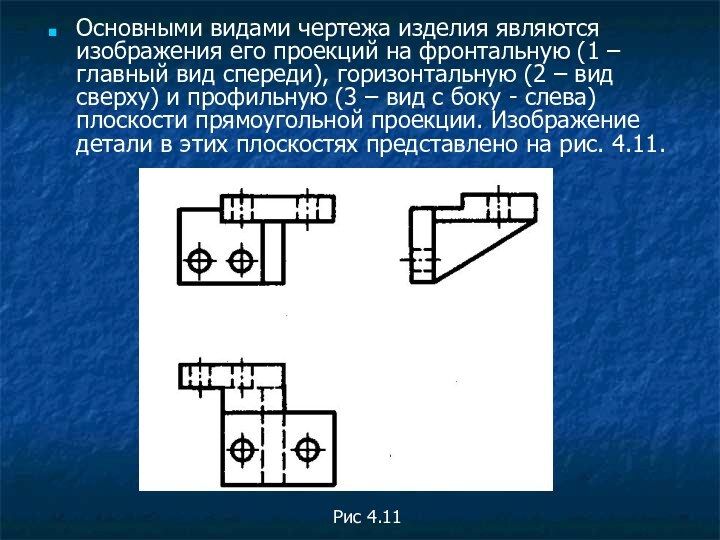
Основными видами чертежа изделия являются изображения его проекций
на фронтальную (1 – главный вид спереди), горизонтальную (2
– вид сверху) и профильную (3 – вид с боку - слева) плоскости прямоугольной проекции. Изображение детали в этих плоскостях представлено на рис. 4.11.
Рис 4.11
Слайд 20
ПРОЕКЦИИ ТОЧКИ
Проецирование точки на три плоскости проекций координатного
угла начинают с получения ее изображения на плоскости H
- горизонтальной плоскости проекций. Для этого через точку А проводят проецирующий луч перпендикулярно плоскости H.
На рисунке перпендикуляр к плоскости Н параллелен оси Oz. Точку пересечения луча с плоскостью Н (точку а) выбирают произвольно. Отрезок Аа определяет, на каком расстоянии находится точка А от плоскости Н, указывая тем самым однозначно положение точки А на рисунке по отношению к плоскостям проекций. Точка а является прямоугольной проекцией точки А на плоскость Н и называется горизонтальной проекцией точки А.
Слайд 22
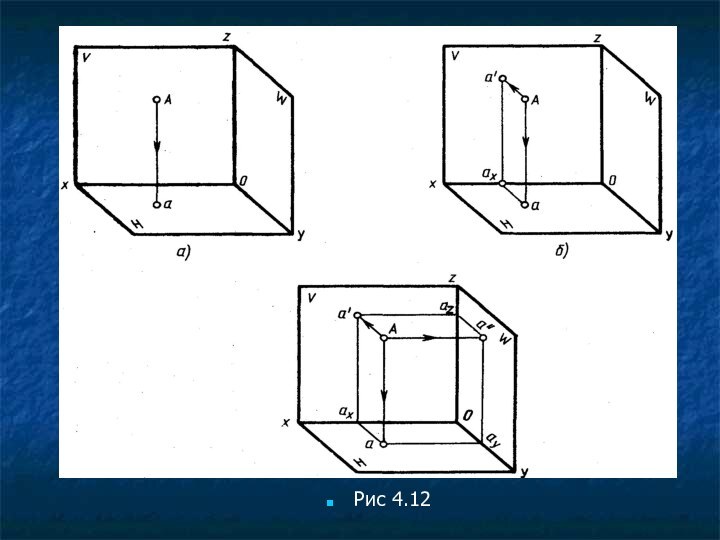
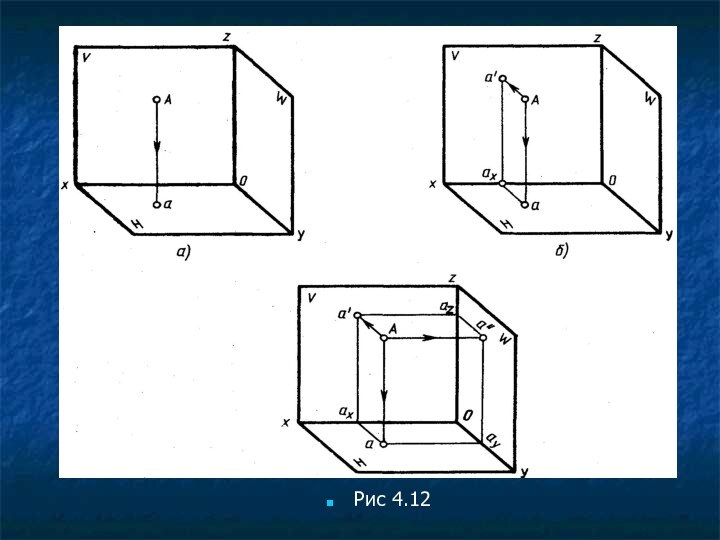
Для получения изображения точки А на плоскости V
(рис. 4.12,б) через точку А проводят проецирующий луч перпендикулярно
фронтальной плоскости проекций V. На рисунке перпендикуляр к плоскости V параллелен оси Оу. На плоскости Н расстояние от точки А до плоскости V изобразится отрезком аах, параллельным оси Оу и перпендикулярным оси Ох. Если представить себе, что проецирующий луч и его изображение проводят одновременно в направлении плоскости V, то когда изображение луча пересечет ось Ох в точке ах, луч пересечет плоскость V в точке а'. Проведя из точки ах в плоскости V перпендикуляр к оси Ох, который является изображением проецирующего луча Аа на плоскости V, в пересечении с проецирующим лучом получают точку а'. Точка а' является фронтальной проекцией точки А, т. е. ее изображением на плоскости V.
Слайд 24
Изображение точки А на профильной плоскости проекций (рис.
4.12, в) строят с помощью проецирующего луча, перпендикулярного плоскости
W. На рисунке перпендикуляр к плоскости W параллелен оси Ох. Проецирующий луч от точки А до плоскости W на плоскости Н изобразится отрезком аау, параллельным оси Ох и перпендикулярным оси Оу. Из точки Оу параллельно оси Oz и перпендикулярно оси Оу строят изображение проецирующего луча аА и в пересечении с проецирующим лучом получают точку а". Точка а" является профильной проекцией точки А, т. е. изображением точки А на плоскости W.
Слайд 26
Точку а" можно построить, проведя от точки а'

отрезок а'аz (изображение проецирующего луча Аа" на плоскости V)
параллельно оси Ох, а от точки аz — отрезок а"аz параллельно оси Оу до пересечения с проецирующим лучом.
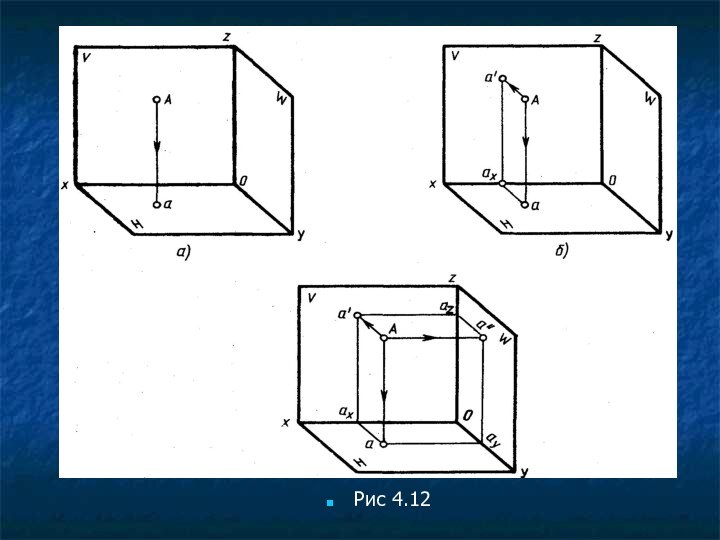
Получив три проекции точки А на плоскостях проекций, координатный угол развертывают в одну плоскость, как показано на рис. 4.11,б, вместе с проекциями точки А и проецирующих лучей, а точку А и проецирующие лучи Аа, Аа' и Аа" убирают. Края совмещенных плоскостей проекций не проводят, а проводят только оси проекций Oz, Оу и Ох, Оу1 (рис. 4.13).
Анализ ортогонального чертежа точки показывает, что три расстояния — Аа', Аа и Аа" (рис. 4.12, в), характеризующие положение точки А в пространстве, можно определить, отбросив сам объект проецирования — точку А, на развернутом в одну плоскость координатном угле (рис. 4.13). Отрезки а'аz, ааy и Оах равны Аа" как противоположные стороны соответствующих прямоугольников (рис. 4.12,в и 4.13). Они определяют расстояние, на котором находится точка А от профильной плоскости проекций. Отрезки а'ах, а"ау1 и Оау равны отрезку Аа, определяют расстояние от точки А до горизонтальной плоскости проекций, отрезки аах, а"аz и Оаy1 равны отрезку Аа', определяющему расстояние от точки А до фронтальной плоскости проекций.
Рис 4.13
Слайд 28
Отрезки Оах, Оау и Оаz, расположенные на осях

проекций, являются графическим выражением размеров координат X, Y и
Z точки А. Координаты точки обозначают с индексом соответствующей буквы. Измерив величину этих отрезков, можно определить положение точки в пространстве, т. е. задать координаты точки.
На эпюре отрезки а'ах и аах располагаются как одна линия, перпендикулярная к оси Ох а отрезки а'аz и a"az — к оси Оz. Эти лини называются линиями проекционной связи. Они пересекают оси проекций в точках ах и аz соответственно. Линия проекционной связи, соединяющая горизонтальную проекцию точки А с профильной, оказалась «разрезанной» в точке ау.
Две проекции одной и той же точки всегда располагаются на одной линии проекционной связи, перпендикулярной к оси проекций.
Для представления положения точки в пространстве достаточно двух ее проекций и заданного начала координат (точка О) На рис. 4.14, б две проекции точки полностью определяют ее положение в пространстве По этим двум проекциям можно построит профильную проекцию точки А. Поэтому в дальнейшем, если не будет необходимости в профильной проекции, эпюры будут построены на двух плоскостях проекций: V и Н.
Рис 4.14
Рис 4.15
Слайд 29
Рассмотрим несколько примеров построения и чтения чертежа точки.
Пример
1. Определение координат точки J заданной на эпюре двумя
проекциях (рис. 4.14). Измеряются три отрезка: отрезок ОвХ (координата X), отрезок bХb (координата Y) и отрезок bХb' (координата Z). Координаты записывают в следующем п рядке: X, Y и Z, после буквенного обозначения точки, например, В20; 30; 15.
Пример 2. Построение точки по заданным координатам. Точка С задана координатами С30; 10; 40. На оси Ох (рис. 4.15) находят точку сх, в которой линия проекционной связи пересекает ось проекций. Для этого по оси Ох от начала координат (точка О) откладывают координату X (размер 30) и получают точку сх. Через эту точку перпендикулярно оси Ох проводят линию проекционной связи и от точки вниз откладывают координату У (размер 10), получают точку с — горизонтальную проекцию точки С. Вверх от точки сх по линии проекционной связи откладывают координату Z (размер 40), получают точку с' — фронтальную проекцию точки С.
Слайд 31
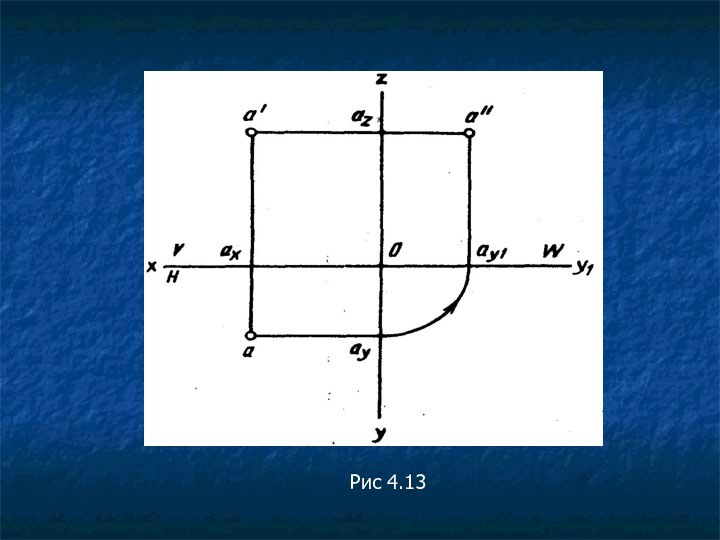
Пример 3. Построение профильной проекции точки по заданным

проекциям. Заданы проекции точки D — d и d'.
Через точку О проводят оси проекций Oz, Oy и Оу1 (рис. 4.16, а). Для построения профильной проекции точки D отточки d' проводят линию проекционной связи, перпендикулярную оси Oz, и продолжают ее вправо за ось Oz. На этой линии будет располагаться профильная проекция точки D. Она будет находиться на таком расстоянии от оси Oz, на каком горизонтальная проекция точки d располагается: от оси Ох, т. е. на расстоянии ddx. Отрезки dzd" и ddx одинаковы, так как определяют одно и то же расстояние — расстояние от точки D до фронтальной плоскости проекций. Это расстояние является координатой У точки D.
Графически отрезок dzd" строят перенесением отрезка ddx с горизонтальной плоскости проекций на профильную. Для этого проводят линию проекционной связи параллельно оси Ох, получают на оси Оу точку dy (рис. 4.16,б). Затем переносят размер отрезка Ody на ось Оу1, проведя из точки О дугу радиусом, равным отрезку Ody, до пересечения с осью Оу1 (рис. 4.16,б), получают точку dy1. Эту точку можно построить и как показано на рис. 4.16, в, проведя прямую под углом 45° к оси Оу из точки dy. Из точки dy1 проводят линию проекционной связи параллельно оси Oz и на ней откладывают отрезок, равный отрезку d'dx, получают точку d".
Перенос величины отрезка dxd на профильную плоскость проекций можно осуществить с помощью постоянной прямой чертежа (рис. 4.16, г). В этом случае линию проекционной связи ddy проводят через горизонтальную проекцию точки параллельно оси Оу1 до пересечения с постоянной прямой, а затем параллельно оси Оу до пересечения с продолжением линии проекционной связи d'dz.
Слайд 32
Частные случаи расположения точек относительно плоскостей проекций
Положение точки

относительно плоскости проекций определяется соответствующей координатой, т. е. величиной
отрезка линии проекционной связи от оси Ох до соответствующей проекции. На рис. 4.17 координата У точки А определяется отрезком аах — расстояние от точки А до плоскости V. Координата Z точки А определяется отрезком а'ах — расстояние от точки А до плоскости Н. Если одна из координат равна нулю, то точка расположена на плоскости проекций. На рис. 4.17 приведены примеры различного расположения точек относительно плоскостей проекций. Координата Z точки В равна нулю, точка находится в плоскости Н. Ее фронтальная проекция находится на оси Ох и совпадает с точкой bх. Координата У точки С равна нулю, точка располагается на плоскости V, ее горизонтальная проекция с находится на оси Ох и совпадает с точкой сх.
Следовательно, если точка находится на плоскости проекций, то одна из проекций этой точки лежит на оси проекций.
Слайд 33
На рис. 4.17 координаты Z и Y точки
D равны нулю, следовательно, точка D находится на оси
проекций Ох и две ее проекции совпадают.
Рис 4.17
Слайд 34
ПРОЕКЦИИ ПРЯМОЙ
При проецировании прямой на какую-либо плоскость проекций
проецирующие лучи, проходящие через точки прямой, образуют проецирующую плоскость,
которая пересекает плоскость проекции по прямой (рис. 4.18). Следовательно, проекцией отрезка будет отрезок прямой. Чаще всего проекция отрезка меньше самого отрезка, так как его проекция (ab) является частью катета прямоугольной: треугольника (ВbМ), а отрезок (АВ) — частью гипотенузы. Так как Mb < MB, то и ab
Рис 4.18
Слайд 35
Коэффициент искажения обозначают буквой К,
К= аb/AB ≤1
Если отрезок
прямой параллелен плоскости проекций, при проецировании образуется прямоугольник, в
котором сам отрезок и его проекция являются противоположными сторонами этого прямоугольника. Следовательно ВС=bс. В этом случае коэффициент искажения К= аb/AB =1, т. е. отрезок проецируется без искажения.
Положение прямой в пространстве можно определить двумя ее точками, поэтому, чтобы задать прямую на эпюре, достаточно задать проекции двух ее точек (рис. 4.18), т.е. проекции отрезка этой прямой. Данные проекции отрезка прямой полностью определяют положение прямой в пространстве.
Рис 4.18
Слайд 36
Сравнивая координаты точек А и В, являющихся концами

отрезка, можно представить себе, как располагается отрезок в пространстве.
Точка В находится выше точки А относительно плоскости Н, так как b'bх>а'ах, т. е. ZB>ZA, и точка В ближе к плоскости V, чем точка А, так как bbx
Различные случаи расположения прямых относительно плоскостей проекций
Прямая общего положения — прямая, не параллельная ни одной из плоскостей проекций (рис. 4.18), т. е. ни одна из проекций этой прямой не параллельна какой-либо оси проекций.
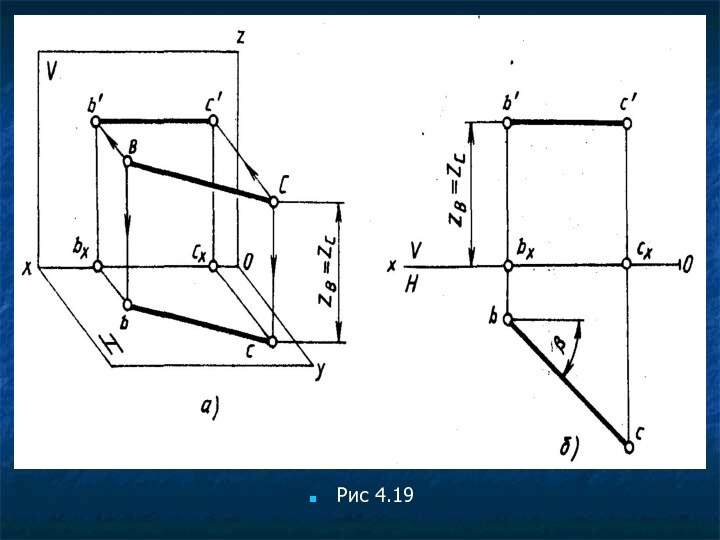
Горизонтальная прямая — прямая, параллельная плоскости Н. Все точки прямой находятся на одинаковом расстоянии от плоскости Н (рис. 4.19, а), т. е. координаты Z всех точек отрезка ВС равны между собой, ВЬ= = Сс — b'bx—c'cx — ZH = Zc- Фронтальная проекция горизонтальной прямой параллельна оси Ох (рис. 4.19,б). Положение второй проекции относительно оси Ох определяется положением самой прямой, Угол наклона горизонтальной прямой к плоскости V — р. На плоскость Н отрезок горизонтальной прямой проецируется в натуральную величину.
Слайд 38
Фронтальная прямая — прямая, параллельная плоскости V. Все
точки прямой находятся на одинаковом расстоянии от плоскости V
(рис. 4.20, а), т. е. координаты Y всех точек отрезка CD равны между собой. Горизонтальная проекция фронтальной прямой параллельна оси Ох (рис. 4.20,б). Положение второй проекции относительно оси Ох определяется положением самой прямой. Угол наклона фронтальной прямой к горизонтальной плоскости H равен α. На плоскость V отрезок фронтальной прямой проецируется в натуральную величину.
Рис 4.20
Слайд 39
Профильная прямая — прямая, параллельная плоскости H. Все
точки прямой находятся на одинаковом расстоянии от плоскости W
(рис. 4.21,а), т. е. координаты X всех точек отрезка DE равны между собой. Фронтальная проекция профильной прямой параллельна оси Oz, а горизонтальная проекция — оси Оу (рис. 4.21,б). Положение профильной проекции определяется положением самой профильной прямой. Угол наклона профильной прямой к плоскости Н — α, к плоскости V — β. На плоскость W отрезок профильной прямой проецируется в натуральную величину.
Рис 4.21
Слайд 40
Прямые, перпендикулярные одной из плоскостей проекций, называют проецирующими
прямыми.
Горизонтально-проецирующая прямая перпендикулярна плоскости H. Проекция такой прямой на
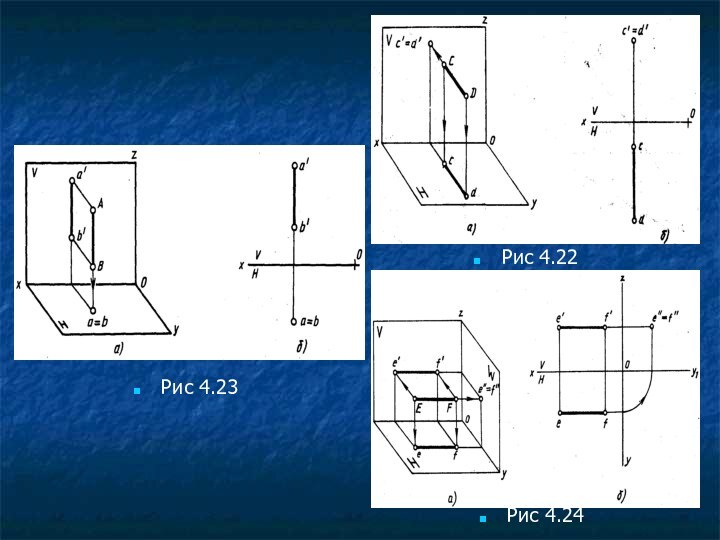
плоскости Н является точкой, а ее фронтальная проекция перпендикулярна оси Ох и параллельна оси Оz (рис. 4.22). На плоскость V прямая проецируется в натуральную величину.
Фронтально-проецирующая прямая перпендикулярна плоскости V. Проекция этой прямой на плоскость V является точкой, а ее горизонтальная проекция перпендикулярна оси Ох и параллельна оси Оу (рис. 4.23). На плоскость Н прямая проецируется в натуральную величину.
Профильно-проецирующая прямая перпендикулярна плоскости W. Проекция этой прямой на плоскость W является точкой. Ее горизонтальная проекция перпендикулярна оси Оу и параллельна оси Ох, а фронтальная — перпендикулярна оси Oz и параллельна оси Ох (рис. 4.24). На плоскости Н и V прямая проецируется в натуральную величину.
Слайд 42
Точка, принадлежащая прямой. Если точка лежит на прямой,
то ее проекции лежат на одноименных проекциях этой прямой
и на одной линии проекционной связи. На рис. 4.25,а точка М лежит на прямой CD. Ее горизонтальная проекция т (рис. 4.25,б) лежит на горизонтальной проекции прямой cd, а фронтальная проекция т' — на фронтальной проекции прямой c'd'.
Обычно по двум проекциям можно определить взаимное расположение точки и прямой. Точка 5 принадлежит прямой CD (рис. 4.25,б), так как ее проекции лежат на продолжении одноименных проекций прямой и на одной линии проекционной связи. Только одна проекция точки F (горизонтальная) лежит на одноименной проекции прямой ей, поэтому точка F не принадлежит прямой CD (рис. 4.25, а и б).
Рис 4.25
Слайд 43
Если прямая параллельна одной из плоскостей проекций, о
взаимном расположении прямой и точки можно получить представление на
плоскости проекций, параллельной данной прямой. Для горизонтальной прямой — на плоскости, для фронтальной прямой — на плоскости V, для профильной прямой — на плоскости W.
На рис. 4.25, в и г показаны частные случаи расположения точки и прямой, когда только две проекции точки F лежат на одноименных проекциях прямой CD, и сама точка F не принадлежит прямой CD, так как третья проекция точки не лежит на проекции прямой.
Слайд 44
Взаимное расположение прямых
Пересекающиеся прямые — прямые, имеющие одну
общую точку. На эпюре одноименные проекции этих прямых пересекаются
в точках, лежащих на одной линии проекционной связи (рис. 4.26, а).
Скрещиваются прямые. Если одноименные проекции прямых пересекаются, но точки пересечения лежат на разных линиях проекционной связи (рис. 4.26,6), то прямые не пересекаются, а скрещиваются. Точки пересечения одноименных проекций (рис. 4.26,б, точки 1' и 2) представляют собой проекции разных точек, которые находятся на одном проецирующем луче и принадлежат разным прямым.
Рис 4.26
Слайд 45
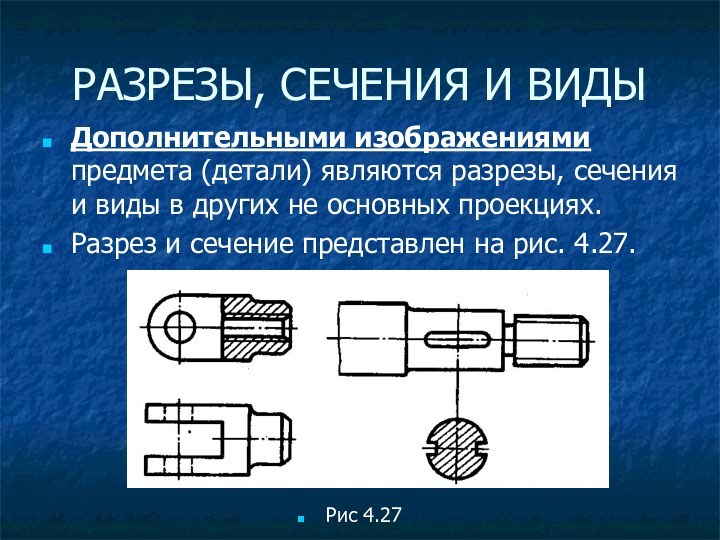
РАЗРЕЗЫ, СЕЧЕНИЯ И ВИДЫ
Дополнительными изображениями предмета (детали) являются
разрезы, сечения и виды в других не основных проекциях.
Разрез и сечение представлен на рис. 4.27.
Рис 4.27
Слайд 46
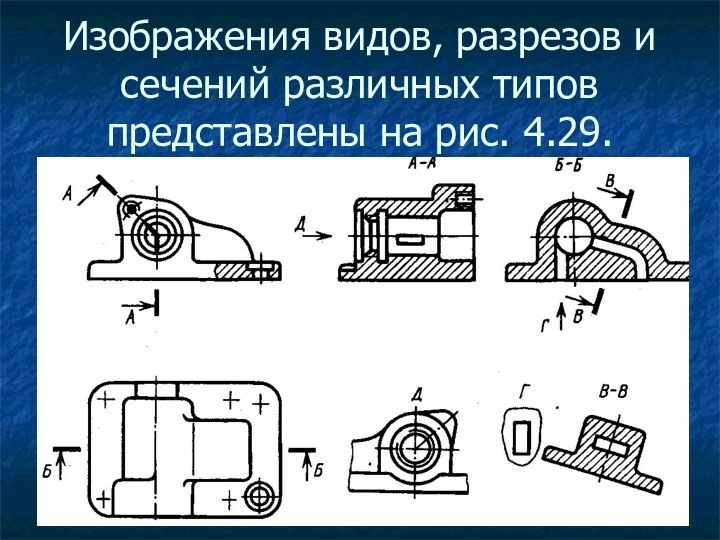
Изображения видов, разрезов и сечений различных типов представлены
на рис. 4.29.
Слайд 47
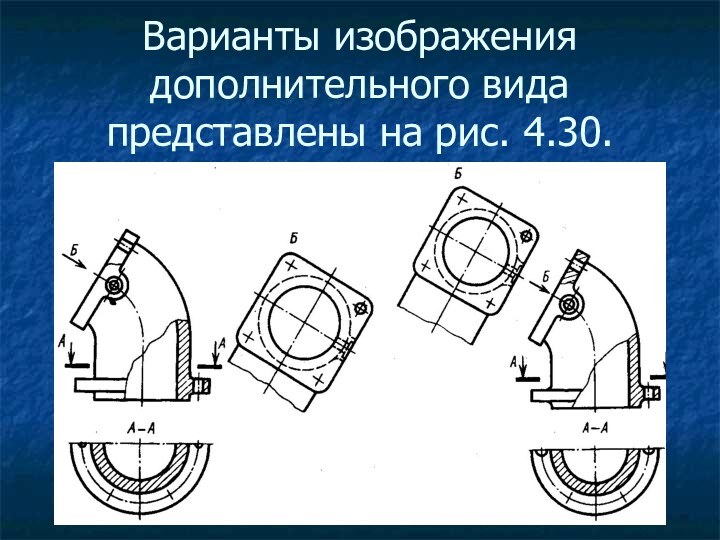
Варианты изображения дополнительного вида представлены на рис. 4.30.
Слайд 48
РАЗМЕРЫ, ПОСТАВЛЯЕМЫЕ НА ЧЕРТЕЖЕ ДЕТАЛИ
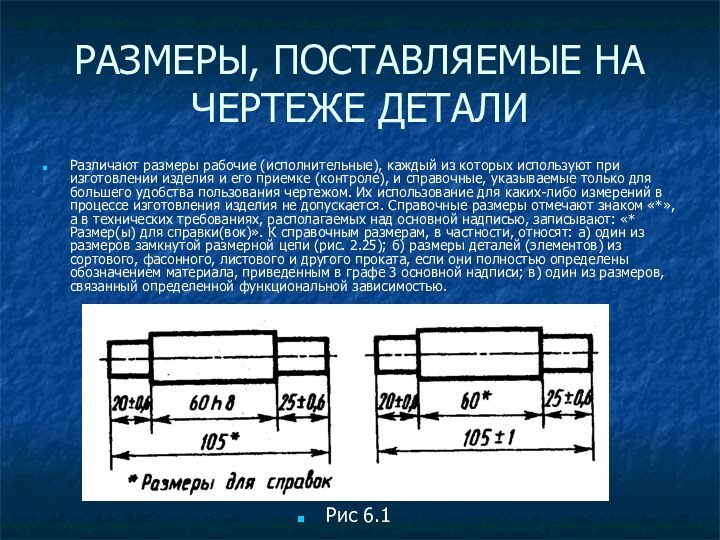
Различают размеры рабочие (исполнительные),
каждый из которых используют при изготовлении изделия и его
приемке (контроле), и справочные, указываемые только для большего удобства пользования чертежом. Их использование для каких-либо измерений в процессе изготовления изделия не допускается. Справочные размеры отмечают знаком «*», а в технических требованиях, располагаемых над основной надписью, записывают: «* Размер(ы) для справки(вок)». К справочным размерам, в частности, относят: а) один из размеров замкнутой размерной цепи (рис. 2.25); б) размеры деталей (элементов) из сортового, фасонного, листового и другого проката, если они полностью определены обозначением материала, приведенным в графе 3 основной надписи; в) один из размеров, связанный определенной функциональной зависимостью.
Рис 6.1
Слайд 49
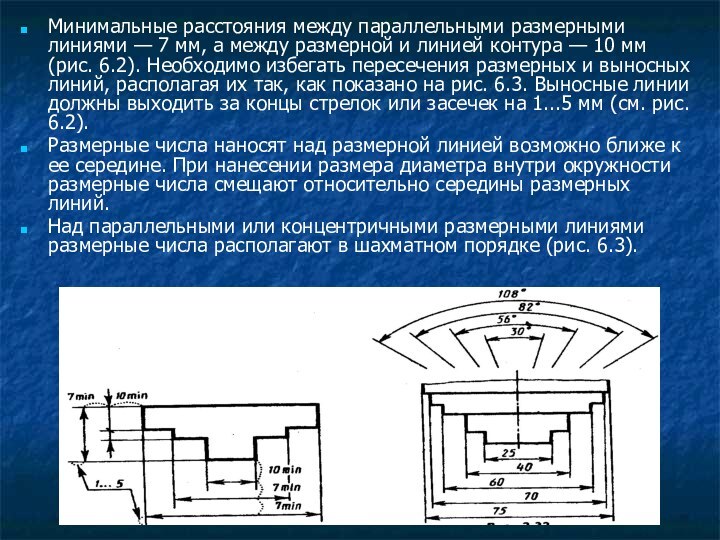
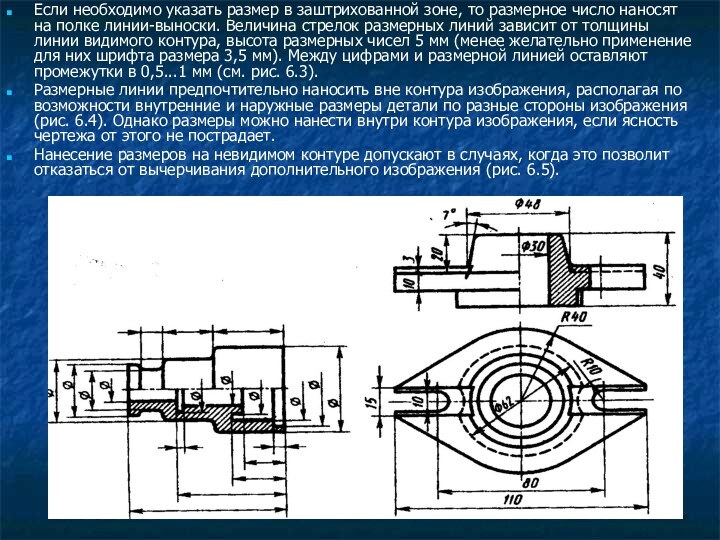
Минимальные расстояния между параллельными размерными линиями — 7
мм, а между размерной и линией контура — 10
мм (рис. 6.2). Необходимо избегать пересечения размерных и выносных линий, располагая их так, как показано на рис. 6.3. Выносные линии должны выходить за концы стрелок или засечек на 1...5 мм (см. рис. 6.2).
Размерные числа наносят над размерной линией возможно ближе к ее середине. При нанесении размера диаметра внутри окружности размерные числа смещают относительно середины размерных линий.
Над параллельными или концентричными размерными линиями размерные числа располагают в шахматном порядке (рис. 6.3).