космос и море, Строенье звёзд и вся Земля, Но
математиков зовёт Известный лозунг:"Прогрессио - движение вперёд!"
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





















"Прогрессио - движение вперёд!"
Актуальность исследования
(Почему это важно для нас?):
В 9 классе мы изучаем прогрессии:
давали определения, научились находить по формулам любой член прогрессии,
сумму первых членов прогрессии. Захотели найти ответы на вопросы:
имеет ли это какое - либо практическое значение
и как давно люди знают последовательности, как возникло это понятие.
Мы подтвердим или опровергнем утверждение того,
что математика – наука очень древняя и возникла она из практических нужд
человека, что алгебра является частью общечеловеческой культуры.
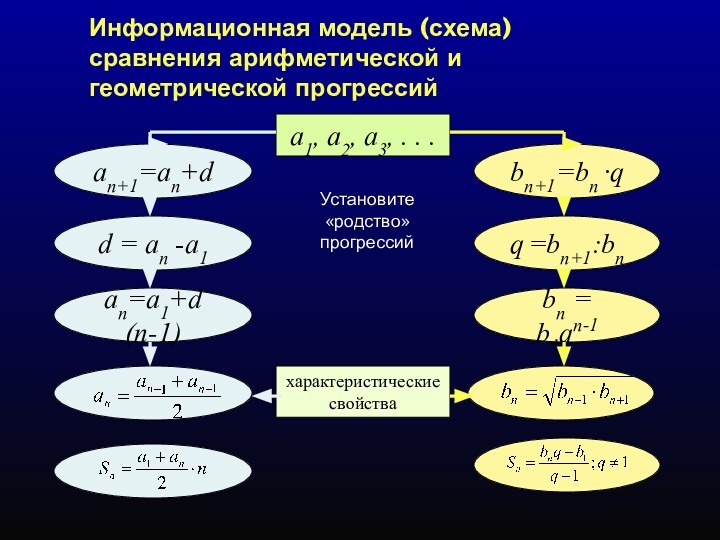
d = an -а1
q =bn+1:bn
характеристические
свойства
Наука о числах
Немного истории
Древняя индийская легенда
b15 = 2·214 = 32 768
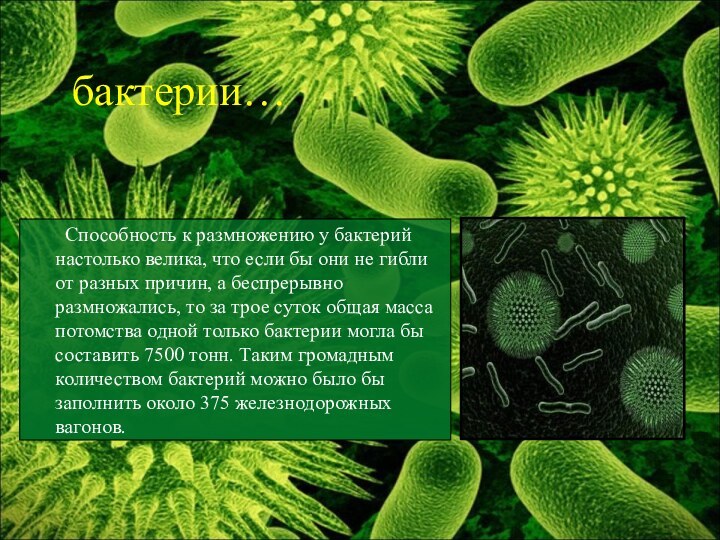
бактерии…
в фармацевтической промышленности (для создания лекарств, вакцин)
в коммунальном
хозяйстве и
природоохранных
мероприятиях
(для очистки сточных
вод,ликвидации
нефтяных пятен)
мухи…
одуванчик…