- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Производная и интеграл для линейных функций. (Глава 1)
Содержание
- 2. Пояснение Сокращенная версия 1 части пособия для показа
- 3. Глава 1. ПРОИЗВОДНАЯ И ИНТЕГРАЛ ДЛЯ ЛИНЕЙНЫХ ФУНКЦИЙ (быстрое начало)
- 4. Основные понятия математического анализа – производная и
- 5. 1.1.1. Линейная функция, по определению, есть функция
- 6. Подчеркнем: такое определение производной относится лишь к
- 7. Геометрически производная есть мера крутизны, то есть,
- 8. Но в таком определении тангенса недостает эмоциональности:
- 9. 1.1.4. Итак, тангенс, угловой коэффициент, производная –
- 10. 1.1.5. Если по оси абсцисс откладывать
- 11. 1.1.7. Терминологическое замечание. Существует магия слов. Подходящее
- 12. 1.1.8. Производную функции принято обозначать как ту
- 13. 1.2. Интеграл 1.2.1. Определенный интеграл, как площадь
- 14. Для частного случая функции – положительной постоянной
- 15. Обозначим верхний предел через x и будем
- 16. Рис. 1.4. Неопределенный интегралДалее. Легко видеть, что
- 17. 1.2.3. Формула Ньютона-Лейбница А сейчас мы увидим,
- 18. Построив затем ее график, пересекающий ось абсцисс
- 19. Это и есть знаменитая формула Ньютона -
- 20. Чрезвычайно важно понять и запомнить следующее. Все,
- 21. Построим прямоугольный треугольник (рис. 1.6, низ), гипотенуза
- 22. 1.2.4. Приложения интеграла: не только площадь Мы
- 23. путьСкорость движенияИнтеграл по времениПроизводная по времениработамощностьИнтеграл по
- 24. Изгибающий моментПеререзывающая силаИнтеграл по длинеПроизводная по длинеФункция
- 25. ЗАКЛЮЧЕНИЕ к главе 1Материал этой главы в
- 26. Мы уже знаем о них:
- 27. Основные сведения, входящие в активное пятно, полезно
- 28. Ариаднина нить для формирования активного
- 29. Скачать презентацию
- 30. Похожие презентации

























Слайд 4 Основные понятия математического анализа – производная и интеграл.
Понять их суть и взаимосвязь – самое главное для
уверенного движения вперед.Заголовок раздела требует пояснения. Для линейного случая эти понятия не нужны – здесь любые задачи элементарно решаются и без них. Пусть Вас это не смущает и не кажется ненужным усложнением. Это – способ «не накладывать трудность на трудность».
Когда задача прозрачна и ответ очевиден, гораздо легче понять и усвоить то, что на самом деле понадобится позже – для задач нетривиальных.
Откладывать знакомство с ним до этого времени – означает следование пословице: на охоту идти – собак кормить.
Слайд 5 1.1.1. Линейная функция, по определению, есть функция первого
порядка. Простейшее ее выражение y = k·x
+ b, а график имеет вид прямой линии. И обратно: любой прямой линии соответствуетвполне определенная линейная функция.
Рис.1.1. График линейной функции
α
b
Δy
Δx
x
y
1.1. Производная
Слайд 6 Подчеркнем: такое определение производной относится лишь к простейшему
частному случаю – линейным функциям. Но для них оно
справедливо при любых, сколь угодно больших приращениях, и для выбранной функции значение производной постоянно при любых значениях аргумента. Более точное определение для общего случая см. в главе 2.1.1.2. Главное свойство линейной функции – в том, что ее приращение пропорционально приращению аргумента:
Коэффициент пропорциональности в этом выражении и есть производная – отношение приращений функции и аргумента:
Слайд 7 Геометрически производная есть мера крутизны, то есть, отношение
величины подъема к величине продвижения вперед. Для лестницы (точнее,
для сопровождающего ее пандуса) – отношение высоты ступеньки к ее длине (по ходу).1.1.3. Тригонометрически производная – это тангенс угла между горизонтальной линией и графиком функции. Или, построив на этих линиях прямоугольный треугольник (см. рис. 1.1) – отношение его вертикального катета к горизонтальному. Обычно говорят: противолежащего катета к прилежащему.
Слайд 8 Но в таком определении тангенса недостает эмоциональности: ничего
не стоит забыть его, или запомнить с точностью до
наоборот, или перепутать с синусом. Для мнемоничности стоит его дополнять для себя менее научным, но более понятным: тангенс – мера крутизны, и чем круче подъем, тем больше тангенс. Синус – тоже мера крутизны, но он меняется от 0 до единицы, а тангенс – до бесконечности.Как видим, для преемственности с элементарной математикой из всей тригонометрии нам пока понадобился один лишь тангенс. В аналитической геометрии ту же величину называют еще угловым коэффициентом.
Попутно - о практической разнице между тангенсом и синусом. Относя высоту подъема к пройденному пути на местности, получаем синус. Определяя же путь по топографической карте, получим тангенс. Ибо путь на местности это гипотенуза, а путь на карте – прилежащий катет. Подъем же, в любом случае – противолежащий катет.
Слайд 9 1.1.4. Итак, тангенс, угловой коэффициент, производная – все
это об одном и том же. И, однако,
это не просто синонимы – между ними есть и различия:тангенс – принадлежность угла,
угловой коэффициент – принадлежность прямой,
производная – понятие, приложимое не только к линейной функции.
Кроме того, если по осям отложены величины с разными размерностями или в разных масштабах, значения тангенса угла и углового коэффициента различны – для перехода от одного к другому обязателен учет масштабных коэффициентов (сколько единиц изображаемой величины укладывается в единицу длины каждой координатной оси). Угловой коэффициент равен тангенсу, умноженному на отношение масштабных коэффициентов функции и аргумента.
Слайд 10 1.1.5. Если по оси абсцисс откладывать время,
а по оси ординат – пройденный путь, то производная
есть скорость движения. Если путь понимать в обобщенном смысле, то так же выражается и скорость любого изменения – например, скорость протекания химической реакции или скорость нагрева воды в чайнике.1.1.6. С другой стороны, производная – это мера влияния аргумента на функцию. В экономике для нее применяют свое название – эластичность (относимое к спросу или предложению) – отношение изменений цены и числа продаж. Впрочем, и сама цена – тоже производная: отношение порции дохода к порции проданного товара. В автоматике – коэффициент усиления или коэффициент передачи. Итак, скорость, эластичность, цена, коэффициент усиления, коэффициент передачи –неполный список синонимов, часть из которых общеупотребительны.
Слайд 11 1.1.7. Терминологическое замечание. Существует магия слов. Подходящее название
– ключ к пониманию. И, наоборот, неудачное – отпугивает,
создает впечатление сложности, чуждости, уводит в сторону от понимания сути.Производная – название весьма неудачное. Оно никак не характеризует обозначаемое понятие – ни его сущность, ни способ получения, ни область применения. Всего лишь некая функция, происходящая от другой функции.
Об этом нужно помнить и противостоять ложному ощущению трудного и непонятного. На самом деле понятием производная (в математическом смысле) владеет каждый человек на житейском уровне, даже если он не слыхал этого слова. И каждому знакомы термины, применяемые в науках и в быту: скорость, крутизна, плотность, цена … , но люди в большинстве не знают или не задумываются о том, что каждое из этих слов – и есть производная на языке конкретной задачи.
Но ведь существует множество объектов, происходящих от других объектов, и к каждой такой паре (исходное– вторичное) приложимо то же название. Например, в химии: вещество В, производное от вещества А – в смысле, не имеющем ничего общего с изучаемым здесь.
Слайд 12 1.1.8. Производную функции принято обозначать как ту же
функцию со штрихом. Например, y′ – производная функции y.
Другое ее обозначение рассмотрим позже.Пока ограничимся приведенными сведениями о производной и вернемся к ней после столь же кратких сведений об интеграле.
Слайд 13
1.2. Интеграл
1.2.1. Определенный интеграл, как площадь
В
отличие от производной, название “интеграл” вполне содержательно. В переводе
– сумма, и в этом или сходных смыслах оно употребляется не только в математике.Причину такого названия раскроем позже (см. гл.2, п.2.2).
Пусть некоторая функция задана своим графиком в прямоугольных координатах (см. рис. 1.2). Назовем определенным интегралом этой функции в пределах от a до b площадь, заключенную между осью абсцисс, графиком функции и двумя вертикальными отрезками с абсциссами a и b, соединяющими график с осью. Величины a и b называют нижним и верхним пределами интегрирования.
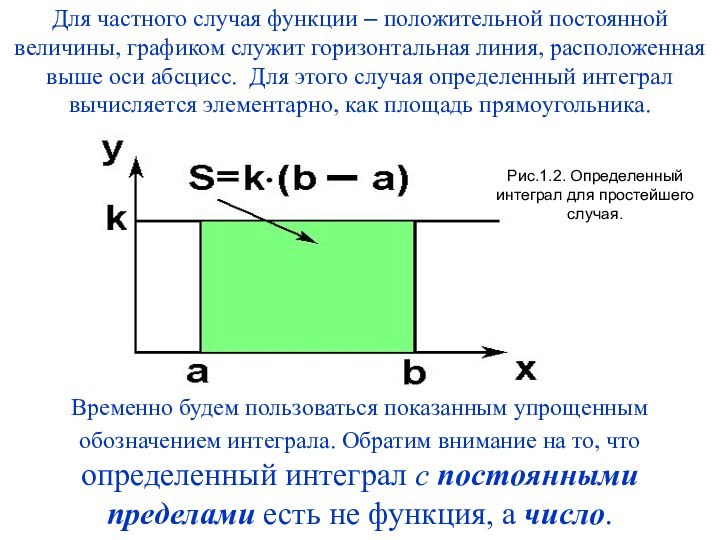
Слайд 14 Для частного случая функции – положительной постоянной величины,
графиком служит горизонтальная линия, расположенная выше оси абсцисс. Для
этого случая определенный интеграл вычисляется элементарно, как площадь прямоугольника.Временно будем пользоваться показанным упрощенным обозначением интеграла. Обратим внимание на то, что определенный интеграл с постоянными пределами есть не функция, а число.
Рис.1.2. Определенный интеграл для простейшего случая.
Слайд 15 Обозначим верхний предел через x и будем непрерывно
двигать его вправо (рис. 1.3, a). Теперь интеграл есть
уже не число, а функция того же аргумента (рис. 1.3, b). Любая точка графика b – это площадь, накопленная под графиком a при движении до текущей абсциссы. Итак, интеграл S(x) на графике a есть площадь, а на графике b – ордината.1.2.2. Интеграл с переменным верхним пределом и взаимная обратность действий дифференцирования и интегрирования
Площадь прямоугольника пропорциональна его длине – расстоянию от нижнего предела, поэтому график – прямая линия, пересекающая ось x в точке a. Какова же ее крутизна? Ясно, что ее угловой коэффициент равен ординате k верхнего графика – коэффициенту пропорциональности между длиной и площадью прямоугольника.
Другими словами, исходная функция (график a) есть производная новой функции (интеграла), выражаемой графиком b.
А значит, интегрирование – вычисление площадей – есть действие, обратное дифференцированию. Отсюда еще одно название для получаемой функции: это первообразная, для которой исходная функция есть производная.
Рис. 1.3. Определенный интеграл
с переменным верхним пределом
Слайд 16
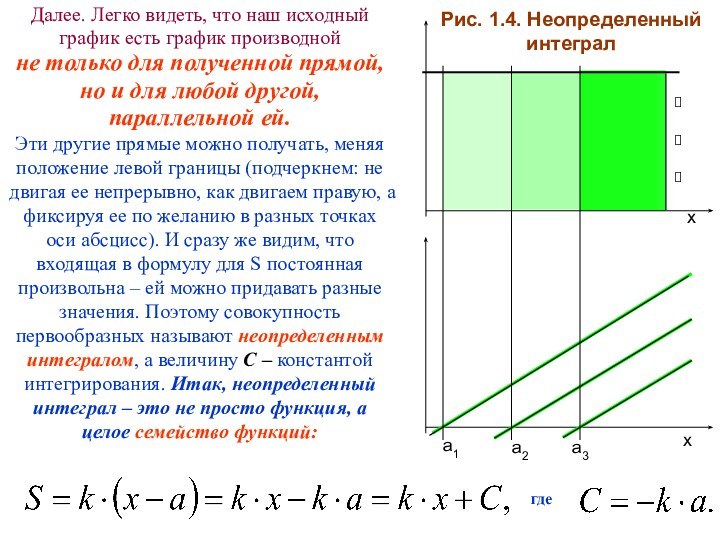
Рис. 1.4. Неопределенный интеграл
Далее. Легко видеть, что наш
исходный график есть график производной
не только для полученной
прямой, но и для любой другой, параллельной ей. Эти другие прямые можно получать, меняя положение левой границы (подчеркнем: не двигая ее непрерывно, как двигаем правую, а фиксируя ее по желанию в разных точках оси абсцисс). И сразу же видим, что входящая в формулу для S постоянная произвольна – ей можно придавать разные значения. Поэтому совокупность первообразных называют неопределенным интегралом, а величину С – константой интегрирования. Итак, неопределенный интеграл – это не просто функция, а целое семейство функций:
где
Слайд 17
1.2.3. Формула Ньютона-Лейбница
А сейчас мы увидим, что
определенный интеграл можно вычислить через посредство неопределенного. Для нашего
частного случая это не нужно – проще вычислить площадь прямоугольника простым умножением.Но ведь когда-то придется переходить к более сложным задачам, с графиками разной формы. Там одним умножением не обойдешься – потребуется универсальный прием, а показать его удобнее на простом примере, где легко сравнить оба подхода.
Потому для начала и воспользовались тем, что площадь прямоугольника умеют определять все – но только для начала.
Выберем для нашей первообразной (рис. 1.5) некую точку отсчета x0 (например, x0=0), не совпадающую ни с одной из заданных границ – пределов интегрирования. В таком совпадении не было бы ничего противозаконного, но лучше не создавать впечатление, что оно для чего-нибудь нужно.
Слайд 18 Построив затем ее график, пересекающий ось абсцисс в
точке x0, отметим на нем точки a и b
для заданных нижнего (левого) и верхнего (правого) пределов. Проведем через них горизонтальные засечки, и покажем расстояние между ними вертикальным отрезком. В каждой из этих точек график изображает площадь прямоугольника в пределах от начала x0 до соответствующего предела. А значит, длина вертикального отрезка между засечками равна искомой площади в заданных границах. Численно – разность значений первообразной на границах интервала – верхнем и нижнем пределах. Отсюда следует формула для вычисления определенного интеграла:Рис. 1.5. Формула Ньютона-Лейбница
или, упростив запись (поскольку результат не зависит от х0):
Слайд 19 Это и есть знаменитая формула Ньютона - Лейбница
(далее именуемая ФНЛ).
ФНЛ на самом деле справедлива не
только для линейных функций, хотя здесь она пока выведена только для них. Для обобщения требуется лишь одно: доказать, что взаимная обратность дифференцирования и интегрирования присуща ВСЕМ, а не только линейным функциям.
Об этом пойдет речь в главе 2.
Смысл ее в том, что для вычисления определенного интеграла вначале находим неопределенный интеграл через действие, обратное дифференцированию, а затем берем разность значений первообразной на верхнем и нижнем пределах.
Слайд 20 Чрезвычайно важно понять и запомнить следующее. Все, что
на исходном графике изображается площадью (повторимся), на новом графике
изображается его ординатами или их разностями. И обратно, все отрезки ординат нижнего рисунка (на рис. 1.3–1.6) – на верхнем изображаются площадями.И еще одно. Для подстановки пределов интегрирования можно брать любую первообразную, но обязательно одну и ту же для обоих. Это настолько само собой разумеется, что в учебниках даже не считают нужным о нем упоминать. А между тем, именно это –
ключевой момент для понимания.
Этой мысли посвящен следующий слайд.
Слайд 21 Построим прямоугольный треугольник (рис. 1.6, низ), гипотенуза которого
– отрезок первообразной между пределами интегрирования.
Он остается самим
собой при любых перемещениях вверх – вниз (то есть, при переходе к другим первообразным), и, естественно, величина его правого катета – а это и есть интеграл – от них не зависит.В этом и состоит смысл ФНЛ на геометрическом языке.
Рис. 1.6. Геометрический смысл теоремы Ньютона-Лейбница
Y=S′
S
S(a, b)
b
a
x
Слайд 22
1.2.4. Приложения интеграла: не только площадь
Мы ввели
интеграл, как площадь под графиком. Но это – лишь
зрительный образ, и понимать его нужно обобщенно. В действительности он может изображать разнообразные величины. И, так же, как для производной, можно сказать, что понятием интеграла каждый владеет на интуитивном уровне. Всегда в паре с ним следует рассматривать величину, получаемую обратным действием. Ниже следует ряд конкретных примеров. Скорость движения есть производная пройденного пути по времени; путь – интеграл скорости по времени.
Мощность есть производная работы по времени; работа есть интеграл мощности по времени.
Скорость нагрева есть производная температуры по времени; температура есть интеграл скорости нагрева по времени.
Эти и другие примеры приведены ниже в виде наглядных схем.
Слайд 23
путь
Скорость движения
Интеграл по времени
Производная по времени
работа
мощность
Интеграл по времени
Производная
по времени
Количество прокачанной нефти
Курс валюты %
Пропускная способность нефтепровода
Уровень инфляции
Интеграл
по времениПроизводная по времени
Интеграл по времени
Производная по времени
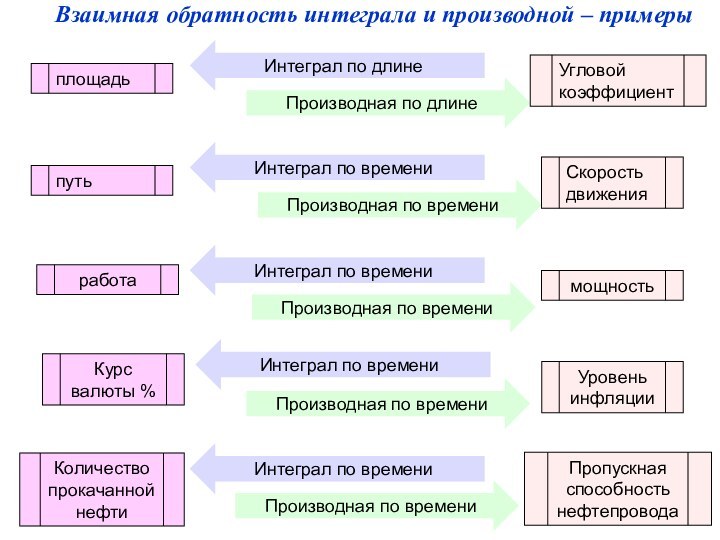
Взаимная обратность интеграла и производной – примеры
площадь
Угловой коэффициент
Интеграл по длине
Производная по длине
Слайд 24
Изгибающий момент
Перерезывающая сила
Интеграл по длине
Производная по длине
Функция распределения
случайной величины
Плотность распределения случайной величины
Интеграл по аргументу
Производная по аргументу
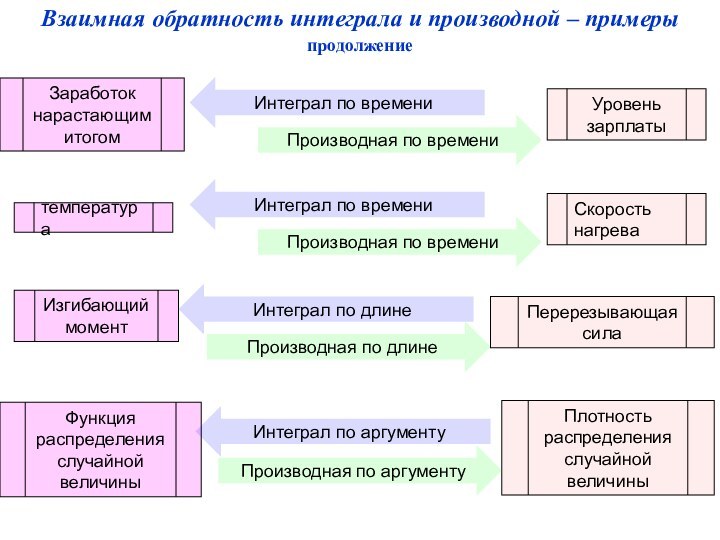
Взаимная
обратность интеграла и производной – примерыпродолжение
температура
Скорость нагрева
Интеграл по времени
Производная по времени
Заработок нарастающим итогом
Уровень зарплаты
Интеграл по времени
Производная по времени
Слайд 25
ЗАКЛЮЧЕНИЕ
к главе 1
Материал этой главы в «обычной»
математике отдельно не рассматривают. Линейные функции – простейший частный
случай, упоминаемый мимоходом. Для них вообще не требуются понятия производной и интеграла и методы дифференциального и интегрального исчислений. И мы применяли их вовсе не для решения линейных задач.Мы как бы повторили элементы аналитической геометрии на другом языке. Но введенный на задачах, где он еще не нужен, этот язык оказывается совсем простым и прозрачным. Тем самым облегчается его освоение там, где он становится необходим. Прозрачность оттого, что нам не потребовались понятия предела, предельного перехода, дифференциала, интегральной суммы. А когда они потребуются, действия с ними облегчатся благодаря уже известным простейшим сведениям о производных и интегралах.
Слайд 26
Мы уже знаем о них:
Производная есть мера крутизны, скорости изменения функции, степени влияния
аргумента на функцию.Интегрирование есть способ определения площадей.
Интегрирование есть действие обратное дифференцированию, и производная интеграла по верхнему пределу равна подынтегральной функции.
Для вычисления определенного интеграла можно использовать неопределенный интеграл через формулу Ньютона-Лейбница.
Вот еще неполный перечень свойств, которые мы не рассматривали, но которые можно узнать из линейного случая.
Интеграл суммы равен сумме интегралов.
Интеграл с одинаковыми пределами равен нулю.
Площадь, образованная графиком с отрицательными ординатами, считается отрицательной.
При перемене местами пределов интегрирования знак интеграла меняется.
Слайд 27 Основные сведения, входящие в активное пятно, полезно представить
в компактном виде по типу опорных сигналов В.Ф. Шаталова.
Они образуют своего рода ариаднину нить, помогающую запомнить навсегда не только их, но и их взаимосвязи (см. следующий слайд).
При этом не нужно зазубривать формулировки. Просто эту картинку нужно держать где-нибудь на видном месте, чтобы она почаще попадалась на глаза, и при каждом удобном случае мысленно восстанавливать ход рассуждений. Запоминание придет, как неизбежный результат понимания.