Презентация на тему Расстояние между точками

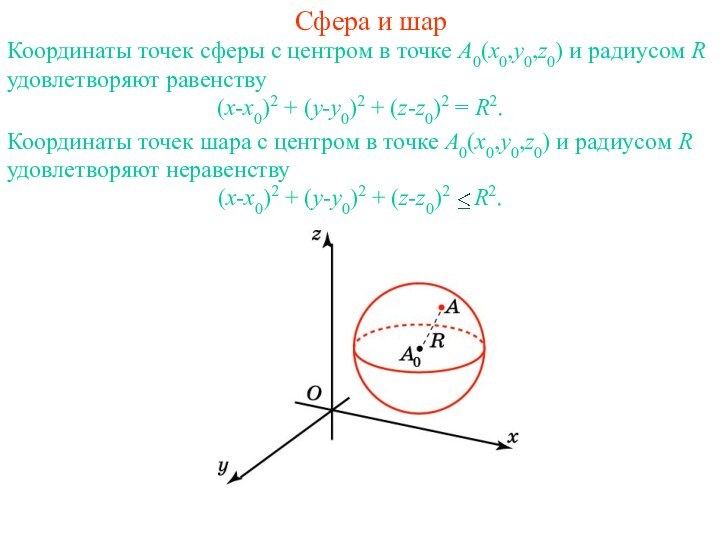
точке A0(x0,y0,z0) и радиусом R удовлетворяют равенству
(x-x0)2 + (y-y0)2

Координаты точек шара с центром в точке A0(x0,y0,z0) и радиусом R удовлетворяют неравенству

(x-x0)2 + (y-y0)2 + (z-z0)2 R2.

и A2(-1, 1, 1), B1(3, 4, 0) и B2(3,

или B (-2, 1, 6) лежит ближе к началу

Ответ: Точка A.

K (3,1,-2). Найдите периметр треугольника MNK.

координаты: A(0, 0, 2), B(0, 2, 0), C(2, 0,

Ответ: Равносторонний.

сферы, заданной уравне­нием:
а) (x - 2)2 + (y +

Ответ: а) C(2,-5,0), R = 3;

точке O(0, 0, 0) и радиусом 1;
б) с

Ответ: а) x2 + y2 +z2 = 1;

б) (x-1)2 + (y+2)2 + (z-3)2 = 16.

O(1, 2, -1), касающейся координатной плоскости: а) Oxy; б)

Ответ: а) (x-1)2 + (y-2)2 + (z+1)2 = 1;

б) (x-1)2 + (y-2)2 + (z+1)2 = 4;

в) (x-1)2 + (y-2)2 + (z+1)2 = 1.

O(3, -2, 1), касающейся координатной прямой: а) Ox; б)

Ответ: а) (x-3)2 + (y+2)2 + (z-1)2 = 5;

б) (x-3)2 + (y+2)2 + (z-1)2 = 10;

в) (x-3)2 + (y+2)2 + (z-1)2 = 13.

координатных плоскостей.
Ответ: 8 сфер (xR)2 + (yR)2 +

y2 + z2=0 задает сферу в пространстве. Найдите ее

Ответ: O(2, 0, 0), R = 2.

сферы x2 + y2 + z2 - 8x +

Ответ: Лежит внутри сферы.

- 1)2 + (y - 2)2 + (z +

Ответ: Не имеют общих точек.

(x-x0)2+(y-y0)2+(z-z0)2R2?
Ответ: а) Точки внутри сферы; б) точки