знание формул, теорем и расчеты. И математика предстает перед
нами как некая абстрактная наука, оперирующая цифрами.Но так ли это на самом деле?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


































Проблема
Цель и задачи проекта
Симметрия
Радиальная симметрия
Поворотная симметрия
Симметрия
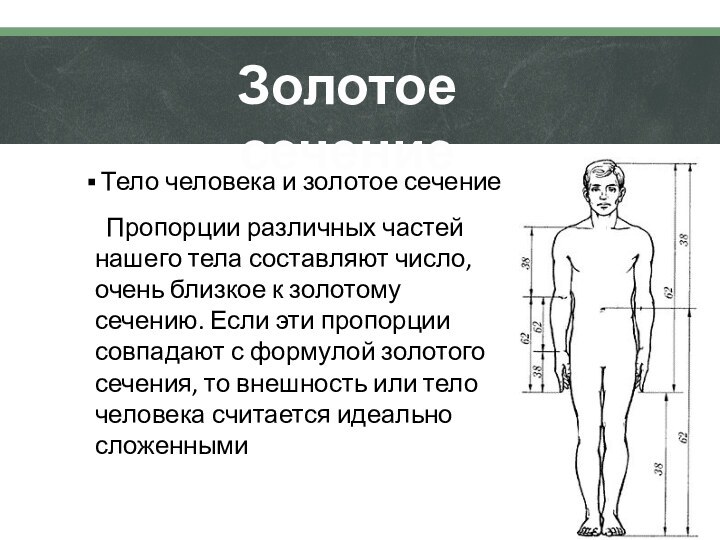
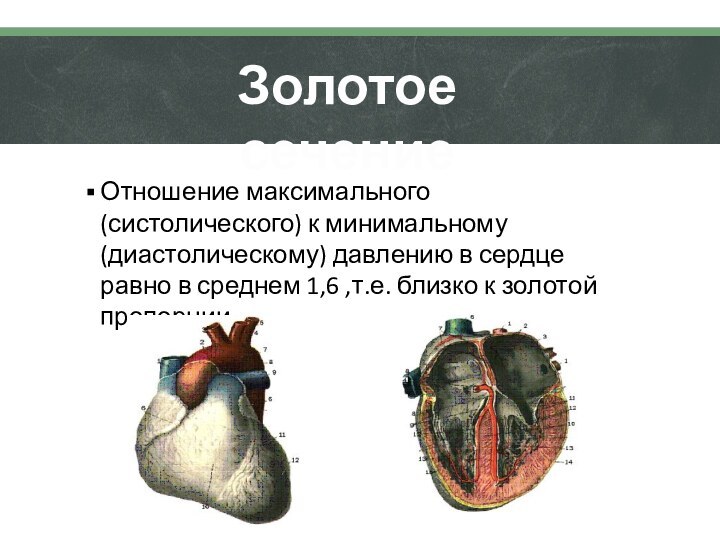
Золотое сечение
В основном соотношение 1/1,618
Золотое сечение
Числа Фибоначчи
Числа Фибоначчи
Числа Фибоначчи
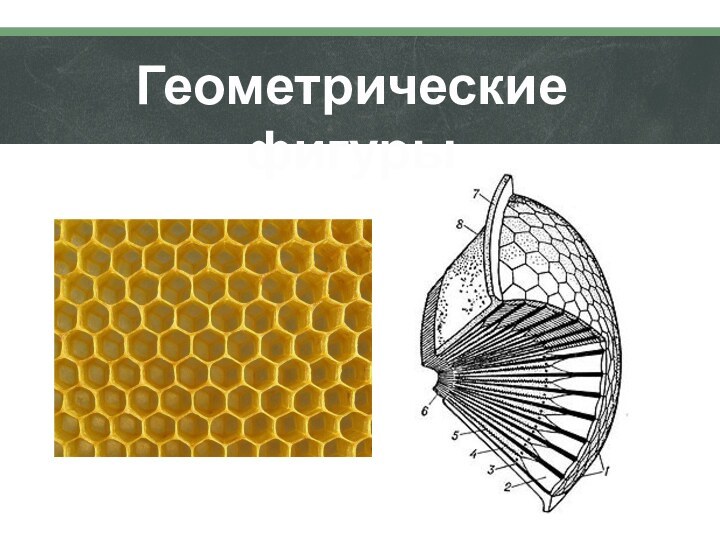
Геометрические фигуры
Геометрические фигуры
Фракталы
Числовые прогрессии
Прогрессия присутствует у одноклеточных организмов. К примеру любая клетка делится на две, эти две делятся на четыре и т.д. То есть это геометрическая прогрессия с коэффициентом 2
Числовые прогрессии
Числовые прогрессии
Заключение