точек на плоскости и конечный набор линий X, соединяющих
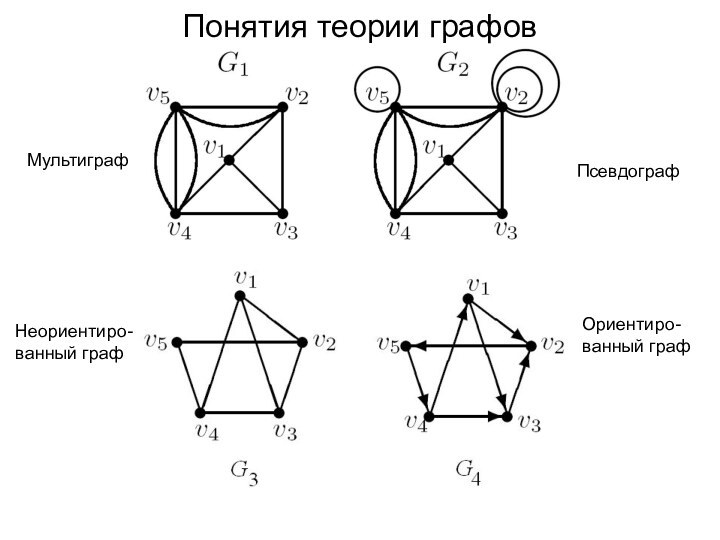
некоторые пары точек из V.Граф состояний - наглядная геометрическая схема, изображающая возможные состояния системы с указанием (в виде стрелок) возможных переходов из состояния в состояние.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть








Матрица инцидентности
(для неориентированного графа)
Матрица
смежности