- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение логических задач
Содержание
- 2. Как решать логические задачи ?Три способа решения логических задач:Средствами алгебры логикиТабличныйС помощью рассуждений
- 3. Решение задач средствами алгебры логикиСхема решения:Изучается условие задачиВводится система обозначенийСоставляется логическая формулаОпределяется значения логической формулы
- 4. Задача «История Нового года»Три друга обсуждали историю
- 5. Задача «История Нового года»Обозначения:Ф – французыР –
- 6. Задача «История Нового года»Логическая формула: (Ф&неЦ + неФ&Ц)&(Р&неК + неР&К)&&(неВ&неФ +Ф&В)= упростим логическую формулувоспользуемся распределительным законом
- 7. Задача «История Нового года»Логическая формула: (Ф&неЦ +
- 8. Задача «История Нового года»Логическая формула:=(неФ&Ц& Р&неК+Ф&неЦ& неР&К)&&(неВ&неФ+Ф&В)==
- 9. Задача «История Нового года»Логическая формула:=(неФ&Ц& Р&неК+Ф&неЦ& неР&К)&&(неВ&неФ+Ф&В)==
- 10. Задача «История Нового года»Логическая формула:=Ц&Р&неК&неВ&неФ формула принимает
- 11. Решение задач табличным способомСхема решения:Результаты рассуждений фиксируются с помощью специально составленных таблиц
- 12. Задача «Новогодние костюмы»На новогодний праздник три друга
- 13. Задача «Новогодние костюмы»
- 14. Решение логических задач с помощью рассужденийЭтим способом обычно решают несложные логические задачи
- 15. Задача «Новогодний подарок»Известно, что на одной двери
- 16. Ответ:Подарок только за первой дверьюЗадача «Новогодний подарок»
- 17. Скачать презентацию
- 18. Похожие презентации
Как решать логические задачи ?Три способа решения логических задач:Средствами алгебры логикиТабличныйС помощью рассуждений
















Слайд 3
Решение задач средствами алгебры логики
Схема решения:
Изучается условие задачи
Вводится
система обозначений
Составляется логическая формула
Определяется значения логической формулы
Слайд 4
Задача «История Нового года»
Три друга обсуждали историю Нового
года, при этом каждый сказал следующее:
Празднование Нового года с
1 января установили во Франции в 45 году до Рождества Христова (Юлием Цезарем)Празднование Нового года с 1 января установили римляне в 1659 году указом Карла IX
Празднование Нового года с 1 января установили во 2 веке и не французы
Оказавшийся рядом знаток истории сказал, что каждый из них прав только в одном из двух высказанных предложений.
Где и в какое время было установлено празднование Нового года с 1 января?
Слайд 5
Задача «История Нового года»
Обозначения:
Ф – французы
Р – римляне
К
– Карл IX в 1659
Ц – Цезарь
В –2
век
Слайд 6
Задача «История Нового года»
Логическая формула:
(Ф&неЦ + неФ&Ц)&(Р&неК
+ неР&К)&
&(неВ&неФ +Ф&В)=
упростим логическую формулу
воспользуемся распределительным законом
Слайд 7
Задача «История Нового года»
Логическая формула:
(Ф&неЦ + неФ&Ц)&(Р&неК
+ неР&К)&
&(неВ&неФ +Ф&В)=
=((Ф&неЦ+неФ&Ц)&Р&неК+(Ф&неЦ+неФ&Ц)&
&неР&К)&(неВ&неФ+Ф&В)=
=(Ф&неЦ&Р&неК+неФ&Ц& Р&неК+Ф&неЦ& &неР&К+неФ&Ц&неР&К)&(неВ&неФ+Ф&В)=
Т.к. Ф&Р=0, Ц&К=0,
то получаем следующую формулу
Слайд 8
Задача «История Нового года»
Логическая формула:
=(неФ&Ц& Р&неК+Ф&неЦ& неР&К)&
&(неВ&неФ+Ф&В)=
= (неФ&Ц&
Р&неК+Ф&неЦ& неР&К)&неВ&неФ+ (неФ&Ц& Р&неК+Ф&неЦ& неР&К)&Ф&В=
Т.к. Ф&неФ=0, неФ&неФ=неФ, Ф&Ф=Ф
то
получаем=неФ&Ц&Р&неК&неВ+Ф&неЦ&неР&К&В=
Слайд 9
Задача «История Нового года»
Логическая формула:
=(неФ&Ц& Р&неК+Ф&неЦ& неР&К)&
&(неВ&неФ+Ф&В)=
= (неФ&Ц&
Р&неК+Ф&неЦ& неР&К)&неВ&неФ+ (неФ&Ц& Р&неК+Ф&неЦ& неР&К)&Ф&В=
Т.к. Ф&неФ=0, неФ&неФ=неФ, Ф&Ф=Ф
то
получаем=неФ&Ц&Р&неК&неВ+Ф&неЦ&неР&К&В,
т.к. К&В=0, то получаем следующую формулу:
Слайд 10
Задача «История Нового года»
Логическая формула:
=Ц&Р&неК&неВ&неФ
формула принимает значение
истинно только при Ц=1, Р=1, К=0, В=0, Ф=0
Ответ:
Празднование
Нового года с 1 января установили римляне в 45 году до Рождества Христова (благодаря введению нового календаря Юлием Цезарем )
Слайд 11
Решение задач
табличным способом
Схема решения:
Результаты рассуждений фиксируются с
помощью специально составленных таблиц
Слайд 12
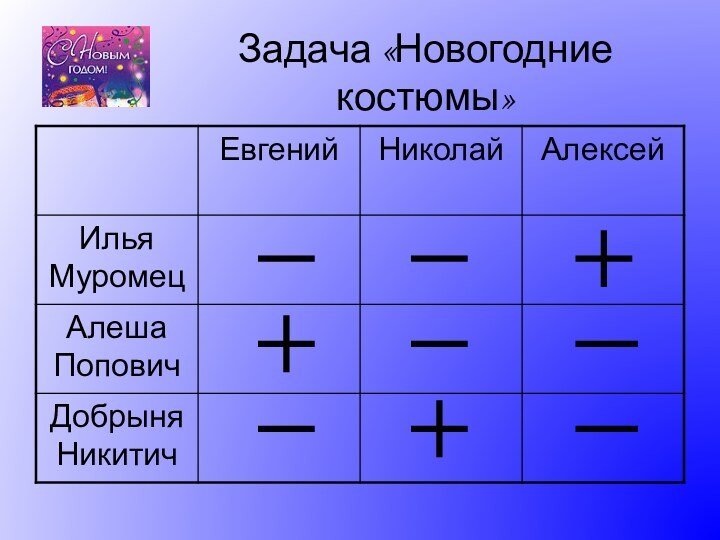
Задача «Новогодние костюмы»
На новогодний праздник три друга –
Евгений, Николай, Алексей, выбрали себе костюмы трех богатырей: Ильи
Муромца, Алеши Попович, Добрыни Никитича.Известно, что:
Евгений – самый высокий
Выбравший костюм Добрыни Никитича меньше ростом, чем выбравший костюм Ильи Муромца
Алексею не подошел костюм Добрыни Никитича
Ни у одного из друзей имена не совпадает с именем богатырей, выбранных костюмов
Какой костюм выбрал каждый из друзей?
Слайд 14
Решение логических задач
с помощью рассуждений
Этим способом обычно
решают несложные логические задачи
Слайд 15
Задача «Новогодний подарок»
Известно, что на одной двери надпись
истинна, а на другой ложна.
Если надпись на первой
двери - "за этой дверью есть подарок", а на второй двери - «подарок за обоими дверьми", то:1) подарок за обоими дверьми;
2) подарок только за второй дверью;
3) подарка нет ни за одной дверью;
4) подарок только за первой дверью;
5) определенно место подарка установить нельзя.
Выберите вариант ответа