Слайд 2
Выбор подходящего метода для решения уравнений зависит от
характера рассматриваемой задачи. Задачи, сводящиеся к решению алгебраических и
трансцендентных уравнений, можно классифицировать по числу уравнений и в зависимости от предлагаемого характера и числа решений (Рисунок 1).
Рисунок 1. Классификация уравнений
Одно уравнение будем называть линейным, алгебраическим или трансцендентным в зависимости от того, имеет ли оно одно решение, n решений или неопределенное число решений. Систему уравнений будем называть линейной или нелинейной в зависимости от математической природы входящих в нее уравнений.
Слайд 3
Нелинейные уравнения можно разделить на 2 класса -

алгебраические и трансцендентные. Алгебраическими уравнениями называют уравнения, содержащие только
алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и другие) называются трансцендентными.
Методы решения нелинейных уравнений делятся на две группы:
точные методы;
итерационные методы.
Точные методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Из школьного курса алгебры известны такие методы для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.
Как известно, многие уравнения и системы уравнений не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраическое уравнение степени выше четвертой. Кроме того, в некоторых случаях уравнение содержит коэффициенты, известные лишь приблизительно, и, следовательно, сама задача о точном определении корней уравнения теряет смысл. Для их решения используются итерационные методы с заданной степенью точности.
Слайд 4
Пусть дано уравнение
где:
Функция
f(x) непрерывна на отрезке [a, b] вместе со своими
производными 1-го и 2-го порядка.
Значения f(x) на концах отрезка имеют разные знаки (f(a) f(b) < 0).
Первая и вторая производные f (x) и f (x) сохраняют определенный знак на всем отрезке.
Условия 1) и 2) гарантируют, что на интервале [a, b] находится хотя бы один корень, а из 3) следует, что f(x) на данном интервале монотонна и поэтому корень будет единственным.
Слайд 5
Решить уравнение итерационным методом значит установить, имеет ли
оно корни, сколько корней и найти значения корней с
нужной точностью.
Всякое значение , обращающее функцию f(x) в нуль, т.е. такое, что:
называется корнем уравнения (1) или нулем функции f(x).
Задача нахождения корня уравнения f(x) = 0 итерационным методом состоит из двух этапов:
отделение корней - отыскание приближенного значения корня или содержащего его отрезка;
уточнение приближенных корней - доведение их до заданной степени точности.
Процесс отделения корней начинается с установления знаков функции f(x) в граничных x = a и x = b точках области ее существования.
Слайд 6
Пример.
Отделить корни уравнения:f(x) - 6х +
2 = 0.
Составим приблизительную схему:
Следовательно, уравнение имеет три
действительных корня, лежащих в интервалах [-3, -1], [0, 1] и [1, 3].
Приближенные значения корней (начальные приближения) могут быть также известны из физического смысла задачи, из решения аналогичной задачи при других исходных данных, или могут быть найдены графическим способом.
В инженерной практике распространен графический способ определения приближенных корней.
Слайд 7
Принимая во внимание, что действительные корни уравнения -
это точки пересечения графика функции f(x) с осью абсцисс,
достаточно построить график функции f(x) и отметить точки пересечения f(x) с осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню. Построение графиков часто удается сильно упростить, заменив уравнение равносильным ему уравнением: ,
где функции f1(x) и f2(x) - более простые, чем функция f(x). Тогда, построив графики функций у = f1(x) и у = f2(x), искомые корни получим как абсциссы точек пересечения этих графиков.
Слайд 8
Пример.
Графически отделить корни уравнения x lg x
= 1.
Уравнение удобно переписать в виде
равенства :l
g x= . Отсюда ясно, что корни уравнения могут быть найдены как абсциссы точек пересечения логарифмической кривой y = lg x и гиперболы y = . Построив эти кривые, приближенно найдем единственный корень уравнения или определим его содержащий отрезок [2, 3].
Слайд 9
Метод половинного деления
Итерационный процесс состоит в последовательном уточнении
начального приближения х0. Каждый такой шаг называется итерацией. В
результате итераций находится последовательность приближенных значений корня х1, х2, ..., хn. Если эти значения с увеличением числа итераций n приближаются к истинному значению корня, то говорят, что итерационный процесс сходится.
Для нахождения корня уравнения, принадлежащего отрезку [a, b],
делим этот отрезок пополам. Если f = 0 , то =
является корнем уравнения. Если f 0 (что, практически,
наиболее вероятно), то выбираем ту из половин или ,
на концах которой функция f(x) имеет противоположные знаки. Новый суженный отрезок а1, b1 снова делим пополам и производим те же самые действия.
Метод половинного деления практически удобно применять для грубого нахождения корня данного уравнения, метод прост и надежен, всегда сходится.
Слайд 10
Пример.
Методом половинного деления уточнить корень уравнения
f(x)
+ 2 – x – 1
= 0
лежащий на отрезке 0, 1.
Последовательно имеем:
f(0) = - 1; f(1) = 1; f(0,5) = 0,06 + 0,25 – 0,5 – 1 = - 1,19;
f(0,75) = 0,32 + 0,84 – 0,75 – 1 = - 0,59;
f(0,875) = 0,59 + 1,34 – 0,88 – 1 = + 0,05;
f(0,8125) = 0,436 + 1,072 – 0,812 – 1 = - 0,304;
f(0,8438) = 0,507 + 1,202 – 0,844 – 1 = - 0,135;
f(0,8594) = 0,546 + 1,270 – 0,859 – 1 = - 0,043 и т. д.
Можно принять
= (0,859 + 0,875)*0,5 = 0,867
Слайд 11
Метод хорд
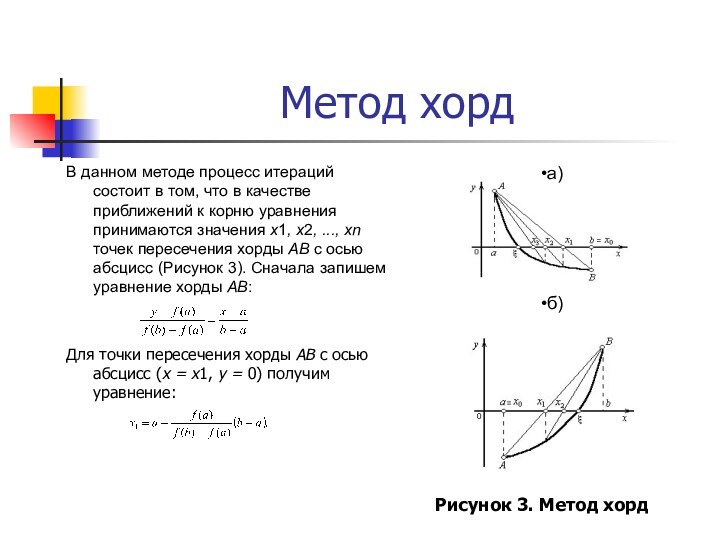
В данном методе процесс итераций состоит в
том, что в качестве приближений к корню уравнения принимаются
значения х1, х2, ..., хn точек пересечения хорды АВ с осью абсцисс (Рисунок 3). Сначала запишем уравнение хорды AB:
Для точки пересечения хорды AB с осью абсцисс (х = х1, y = 0) получим уравнение:
Рисунок 3. Метод хорд
Слайд 12
Пусть для определенности f (x) > 0 при а х b
(случай f (x)
уравнение в виде ‑ f(x) = 0). Тогда кривая у = f(x) будет выпукла вниз и, следовательно, расположена ниже своей хорды АВ. Возможны два случая: 1) f(а) > 0 (Рисунок 3, а) и 2) f(b) < 0 (Рисунок 3, б).
В первом случае конец а неподвижен и последовательные приближения: x0 = b
образуют ограниченную монотонно убывающую последовательность, причем
Во втором случае неподвижен конец b, а последовательные приближения: x0 = а;
образуют ограниченную монотонно возрастающую последовательность, причем
Слайд 13
Обобщая эти результаты, заключаем:
неподвижен тот конец, для
которого знак функции f (х) совпадает со знаком ее
второй производной f (х);
последовательные приближения xn лежат по ту сторону корня , где функция f (х) имеет знак, противоположный знаку ее второй производной f (х).
Итерационный процесс продолжается до тех пор, пока не будет обнаружено, что < ,
где - заданная предельная абсолютная погрешность.
Слайд 14
Пример.
Найти положительный корень уравнения
f(x) – 0,2
– 0,2 х – 1,2 = 0 с
точностью = 0,01.
Прежде всего, отделяем корень. Так как f (1) = -0,6 < 0 и f (2) = 5,6 > 0,
то искомый корень лежит в интервале [1, 2]. Полученный интервал велик, поэтому разделим его пополам. Так как
f (1,5) = 1,425 > 0, то 1< < 1,5.
Так как f (x) = 6 x – 0,4 > 0 при 1 < х < 1,5 и f (1,5) > 0, то воспользуемся формулой для решения поставленной задачи:
= 1,15; x1 – x0 = 0,15 > ,
следовательно, продолжаем вычисления; f (х1) = -0,173;
= 1,190;
x2 – x1 = 0,04 > , f (х2) = -0,036;
= 1,198;
x3 – x2 = 0,008 < .
Таким образом, можно принять = 1,198 с точностью = 0,01.
Заметим, что точный корень уравнения = 1,2.
Слайд 15
Метод Ньютона.
Отличие этого итерационного метода от предыдущего состоит
в том, что вместо хорды на каждом шаге проводится
касательная к кривой y = f(x) при x = хi и ищется точка пересечения касательной с осью абсцисс (Рисунок 4). При этом не обязательно задавать отрезок [а, b], содержащий корень уравнения , достаточно найти лишь некоторое начальное приближение корня x = х0.
Применяя метод Ньютона, следует руководствоваться следующим правилом: в качестве исходной точки х0 выбирается тот конец интервала [а, b], которому отвечает ордината того же знака, что и знак f (х).
Рисунок 4. Метод Ньютона
Слайд 16
Уравнение касательной, проведенной к кривой y = f(x)
через точку В0 с координатами х0 и f(х0), имеет
вид:
Отсюда найдем следующее приближение корня х1 как абсциссу точки пересечения касательной с осью Ох (y = 0):
Аналогично могут быть найдены и следующие приближения как точки пресечения с осью абсцисс касательных, проведенных в точках В1, В2 и так далее. Формула для i +1 приближения имеет вид:
Для окончания итерационного процесса может быть использовано или условие f(xi) < , или условие близости последовательных приближений < .
Итерационный процесс сходится если f(х0) f (х0) > 0.
Слайд 18
Метод простой итерации
Для использования метода итерации исходное нелинейное
уравнение f(х) = 0 заменяется равносильным уравнением x =
(x). Пусть известно начальное приближение корня х = х0. Подставляя это значение в правую часть уравнения , получим новое приближение:х1 = (х0).
Далее, подставляя каждый раз новое значение корня в , получаем последовательность значений:
Геометрически метод итерации может быть пояснен следующим образом. Построим на плоскости хОу графики функций у = х и у = (х). Каждый действительный корень уравнения является абсциссой точки пересечения М кривой у = (х) с прямой у = х (Рисунок 6, а).
Слайд 19
Отправляясь от некоторой точки А0 [x0, (x0)],
строим ломаную А0В1А1В2А2... (“лестница”), звенья которой попеременно параллельны оси
Ох и оси Оу, вершины А0, А1, А2, ...лежат на кривой у= (х), а вершины В1, В2, В3, …, - на прямой у = х. Общие абсциссы точек А1 и В1, А2 и В2, ..., очевидно, представляют собой соответственно последовательные приближения х1, х2, ... корня .
Возможен также другой вид ломаной А0В1А1В2А2 ... – «спираль» (Рисунок 6, б). Решение в виде «лестницы» получается, если производная (х) положительна, а решение в виде «спирали», если (х) отрицательна.
На Рисунке 6, а, б кривая у = (х) в окрестности корня - пологая, то есть <1, и процесс итерации сходится.
Слайд 20
Однако, если рассмотреть случай, где
>1, то процесс итерации может быть расходящимся (Рисунок 7).
Поэтому для практического применения метода итерации нужно выяснить достаточные условия сходимости итерационного процесса.
Теорема: Пусть функция (х) определена и дифференцируема на отрезке [a, b], причем все ее значения (х) [a, b].
Тогда, если существует правильная дробь q такая, что q < 1
при a < x < b, то: 1) процесс итерации
сходится независимо от начального значения х0 [a, b];
2) предельное значение является единственным корнем уравнения х = (х) на отрезке [a, b].
Слайд 21
Пример.
f(x) – x – 1 =
0 имеет корень [1, 2], так как
f(1) = - 1 < 0 и f(2) = 5 > 0.
Уравнение можно записать в виде х = – 1. Здесь (х) = – 1 и (х) = 3 ;
Поэтому (х) 3 при 1 х 2
и, следовательно, условия сходимости процесса итерации не выполнены.
Если записать уравнение в виде
то будем иметь:
Отсюда при 1 х 2 и значит, процесс итерации
для уравнения быстро сойдется.
Уравнение
Слайд 22
Найдем корень уравнения (10) с точностью до
. Вычисляем последовательные приближения хn с
одним запасным знаком по формуле
Найденные значения помещены в Таблицу 1:
Таблица 1
Значения последовательных приближений xi.
С точностью до можно положить = 1,324.

















![Решение нелинейных уравнений Отправляясь от некоторой точки А0 [x0, (x0)], строим ломаную А0В1А1В2А2... (“лестница”),](/img/tmb/14/1308011/e771f81dd8f88b575cb7ed870ec9ba49-720x.jpg)