Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Решение показательных неравенств

Содержание

2. Аннотация урокаТема «
3. Показательные неравенстваих типы и методы решения
4. Альберт Эйнштейн« Мне приходится делить своё время
5. Структура урока Организационный момент Постановка целей
6. Организационный момент Приветствовать учащихся Отметить в классном журнале фамилии учащихся , отсутствующих на уроке
7. Постановка целей и задач Объявить учащимся в
8. Цели урокаОбразовательные Формирование понятия показательного неравенства Ознакомление
9. Цели урокаВоспитательныеВоспитание трудолюбияВоспитание самостоятельности в достижении целиФормирование вычислительных навыковФормирование эстетических навыков при оформлении записей
10. Цели урокаРазвивающиеРазвитие мыслительной деятельностиРазвитие творческой инициативыРазвитие познавательной активностиРазвитие речи и памяти
11. Задачи урокаПовторить свойства показательной функцииПовторить правила решения
12. Тип урокаУрок формирования новых знаний
13. Вид урокаУрок - лекция
14. Методы обученияОбъяснительно-иллюстративныйЭвристическийПоисковыйПроблемный
15. Технология обученияИнформационно-коммуникационная технология, основанная на проблемном обучении
16. План лекцииПовторение свойств показательной функцииПростейшие показательные неравенстваПоказательные
17. Повторение ранее изученного материалаРешить на доске и
18. Повторение свойств показательной функции
19. монотонно убывает на RОсь Ох является горизонтальной
22. возрастающая убывающая возрастающая убывающая
23. Введение новых знаний
24. Пусть а – данное положительное, не равное
25. Решением неравенства с неизвестным х называют число
26. Решить неравенство – значит, найти все его решения или показать, что их нет.
27. y=b, b00101х0х0
29. х0х1y=b, b>0х2Если a > 1 и b
30. х0х1y=b, b>01Если a > 1 и b
32. возрастает на всей области определения, Решение:
33. Решение:убывает на всей области определения,
34. Решение: возрастает на всей области определения,
35. возрастает на всей области определения
36. возрастает на всей области определения,
37. возрастает на всей области определения
38. Вернёмся к переменной х возрастает при всех х из области определения
39. возрастает на всей области определения
40. убывает на всей области определения
41. Вернёмся к переменной х убывает на всей области определения
42. Вернёмся к переменной х возрастает на всей области определения
43. Решим каждое утверждение совокупности отдельно.
44. ПроверкаПроверка показала, что х=1, х=3, х=1,5 являются решениями уравнения, а х=2 не является решением уравнения.
45. Закрепление знаний Какие неравенства называются показательными ?
46. Итог урока Выяснить , что нового узнали
47. Домашнее задание Учебник для 10 класса «Алгебра
48. Показательные неравенстваих типы и методы решения
49. Скачать презентацию
50. Похожие презентации

Аннотация урокаТема « Показательные неравенства» является важнейшей темой математики . По учебнику С. М. Никольского она изучается в 10 классе и на её изучение по планированию отводится 2 часа :

Главная
Математика
Решение показательных неравенств

Урок – лекция по теме : «Показательные неравенства, их

Аннотация урокаТема « Показательные неравенства» является важнейшей темой

Показательные неравенстваих типы и методы решения

Альберт Эйнштейн« Мне приходится делить своё время между политикой и решением уравнений

Структура урока Организационный момент Постановка целей и задач План лекции Актуализация

Организационный момент Приветствовать учащихся Отметить в классном журнале фамилии учащихся , отсутствующих на уроке

Постановка целей и задач Объявить учащимся в начале урока его цели и

Цели урокаОбразовательные Формирование понятия показательного неравенства Ознакомление учащихся с типами показательных неравенств

Цели урокаВоспитательныеВоспитание трудолюбияВоспитание самостоятельности в достижении целиФормирование вычислительных навыковФормирование эстетических навыков при оформлении записей

Цели урокаРазвивающиеРазвитие мыслительной деятельностиРазвитие творческой инициативыРазвитие познавательной активностиРазвитие речи и памяти

Задачи урокаПовторить свойства показательной функцииПовторить правила решения квадратных и дробно – рациональных

Методы обученияОбъяснительно-иллюстративныйЭвристическийПоисковыйПроблемный

Технология обученияИнформационно-коммуникационная технология, основанная на проблемном обучении

План лекцииПовторение свойств показательной функцииПростейшие показательные неравенстваПоказательные неравенства, сводящиеся к простейшимПоказательные неравенства,

Повторение ранее изученного материалаРешить на доске и в тетрадях : а) квадратные

Повторение свойств показательной функции

монотонно убывает на RОсь Ох является горизонтальной асимптотоймонотонно возрастает на R8. При

возрастающая убывающая возрастающая убывающая

Пусть а – данное положительное, не равное единице число и b –

Решением неравенства с неизвестным х называют число х0, при подстановке которого в

Решить неравенство – значит, найти все его решения или показать, что их нет.

х0х1y=b, b>0х2Если a > 1 и b > 0, то для каждого

х0х1y=b, b>01Если a > 1 и b > 0, то для каждого

возрастает на всей области определения, Решение:

Решение:убывает на всей области определения,

Решение: возрастает на всей области определения,

Вернёмся к переменной х возрастает при всех х из области определения

Вернёмся к переменной х убывает на всей области определения

Вернёмся к переменной х возрастает на всей области определения

Решим каждое утверждение совокупности отдельно.

ПроверкаПроверка показала, что х=1, х=3, х=1,5 являются решениями уравнения, а х=2 не является решением уравнения.

Закрепление знаний Какие неравенства называются показательными ? Когда показательное неравенство имеет решение

Итог урока Выяснить , что нового узнали учащиеся на этом уроке Выставить

Домашнее задание Учебник для 10 класса «Алгебра и начала анализа « автор

Слайды презентации

Слайд 2 Аннотация урока
Тема « Показательные

Аннотация урокаТема « Показательные неравенства» является важнейшей темой математики

неравенства» является важнейшей темой математики . По учебнику С.

М. Никольского она изучается в 10 классе и на её изучение по планированию отводится 2 часа : 1час-Простейшие показательные неравенства ; 1 час – Неравенства , сводящиеся к простейшим заменой неизвестного . За это время нужно познакомить учащихся с новым и очень объёмным материалом , научить их решать все типы показательных неравенств и хорошо отработать эти навыки и умения .Поэтому уроки формирования новых знаний в виде лекций с применением информационно-коммуникационной технологии позволяют решать эти проблемы быстро и с большим успехом .

Слайд 3 Показательные неравенства
их типы и методы решения

Слайд 4 Альберт Эйнштейн
« Мне приходится делить своё время между

Альберт Эйнштейн« Мне приходится делить своё время между политикой и решением

политикой и решением уравнений и неравенств . Однако решение

уравнений и неравенств , по-моему, гораздо важнее , потому что политика существует только для данного момента , а уравнения и неравенства будут существовать вечно .»

Слайд 5 Структура урока
Организационный момент
Постановка целей и задач

План лекции
Актуализация знаний учащихся в виде повторения ранее

изученного материала
Введение новых знаний
Закрепление знаний в форме собеседования
Подведение итогов урока
Домашнее задание

Слайд 6 Организационный момент
Приветствовать учащихся
Отметить в классном журнале

фамилии учащихся , отсутствующих на уроке

Слайд 7 Постановка целей и задач
Объявить учащимся в начале

Постановка целей и задач Объявить учащимся в начале урока его цели

урока его цели и задачи
Познакомить учащихся с

планом лекции и записать его в тетради

Слайд 8 Цели урока
Образовательные
Формирование понятия показательного неравенства
Ознакомление учащихся

Цели урокаОбразовательные Формирование понятия показательного неравенства Ознакомление учащихся с типами показательных

с типами показательных неравенств
Формирование умений и навыков решения

показательных неравенств

Слайд 9 Цели урока
Воспитательные
Воспитание трудолюбия
Воспитание самостоятельности в достижении цели
Формирование вычислительных

навыков
Формирование эстетических навыков при оформлении записей

Слайд 10 Цели урока
Развивающие
Развитие мыслительной деятельности
Развитие творческой инициативы
Развитие познавательной активности
Развитие

речи и памяти

Слайд 11 Задачи урока
Повторить свойства показательной функции
Повторить правила решения квадратных

Задачи урокаПовторить свойства показательной функцииПовторить правила решения квадратных и дробно –

и дробно – рациональных неравенств
Отработать алгоритм решения простейших показательных

неравенств
Научить учащихся различать типы показательных неравенств
Научить учащихся решать показательные неравенства

Слайд 12 Тип урока
Урок формирования новых знаний

Слайд 13 Вид урока
Урок - лекция

Слайд 14 Методы обучения
Объяснительно-иллюстративный
Эвристический
Поисковый
Проблемный

Слайд 15 Технология обучения
Информационно-коммуникационная технология,
основанная на проблемном обучении

Слайд 16 План лекции
Повторение свойств показательной функции
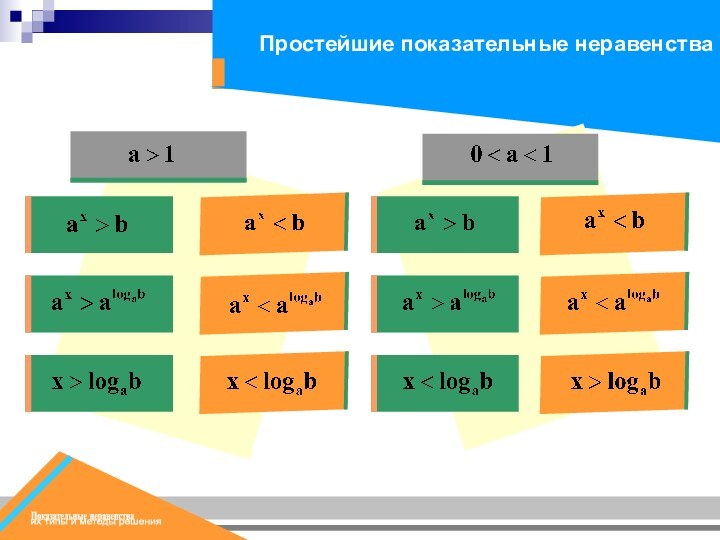
Простейшие показательные неравенства
Показательные неравенства,

сводящиеся к простейшим
Показательные неравенства, сводящиеся к квадратным неравенствам
Однородные показательные

неравенства первой степени
Однородные показательные неравенства второй степени
Показательные неравенства, сводящиеся к рациональным неравенствам
Показательные нестандартные неравенства

Слайд 17 Повторение ранее изученного материала
Решить на доске и в

Повторение ранее изученного материалаРешить на доске и в тетрадях : а)

тетрадях :
а) квадратные неравенства :
х²

– 2х – 1 ≥ 0
х² – 2х - 3 ≤ 0
б) дробно- рациональное неравенство :
( х – 5) \ ( х - 2 ) ≤ 0

Слайд 18 Повторение свойств показательной функции

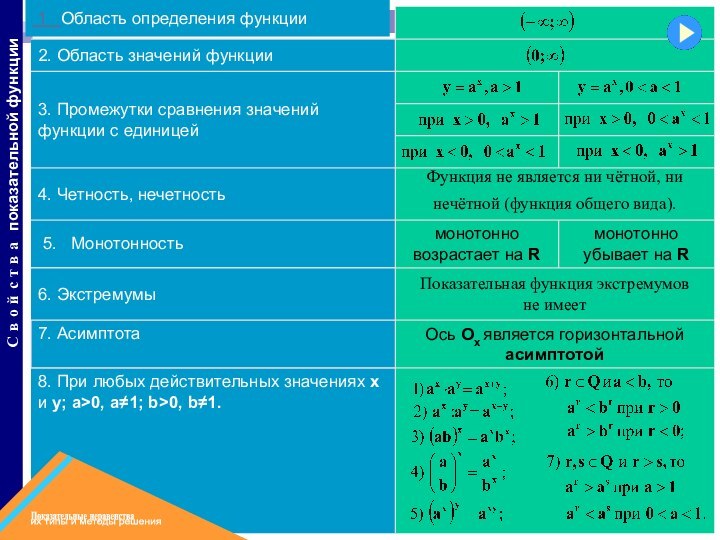
Слайд 19 монотонно убывает на R
Ось Ох является горизонтальной асимптотой
монотонно

монотонно убывает на RОсь Ох является горизонтальной асимптотоймонотонно возрастает на R8.

возрастает на R
8. При любых действительных значениях х и

у; a>0, a≠1; b>0, b≠1.

7. Асимптота

6. Экстремумы

5. Монотонность

4. Четность, нечетность

3. Промежутки сравнения значений функции с единицей

2. Область значений функции

1 Область определения функции

С в о й с т в а показательной функции

Показательные неравенства

их типы и методы решения

Показательная функция экстремумов не имеет

Функция не является ни чётной, ни нечётной (функция общего вида).

Слайд 20

Слайд 21

Слайд 22 возрастающая
убывающая
возрастающая
убывающая

Слайд 23 Введение новых знаний

Слайд 24 Пусть а – данное положительное, не равное единице

число и b – данное действительное число. Тогда неравенства

ax > b (ax ≥ b) и ax < b (ax ≤ b) называются простейшими показательными неравенствами.

Слайд 25 Решением неравенства с неизвестным х называют число х0,

Решением неравенства с неизвестным х называют число х0, при подстановке которого

при подстановке которого в неравенство получается верное числовое неравенство.

Слайд 26 Решить неравенство –
значит, найти все его решения

или показать, что их нет.

Слайд 27 y=b, b0
0
1
0
1
х0
х0

Слайд 28

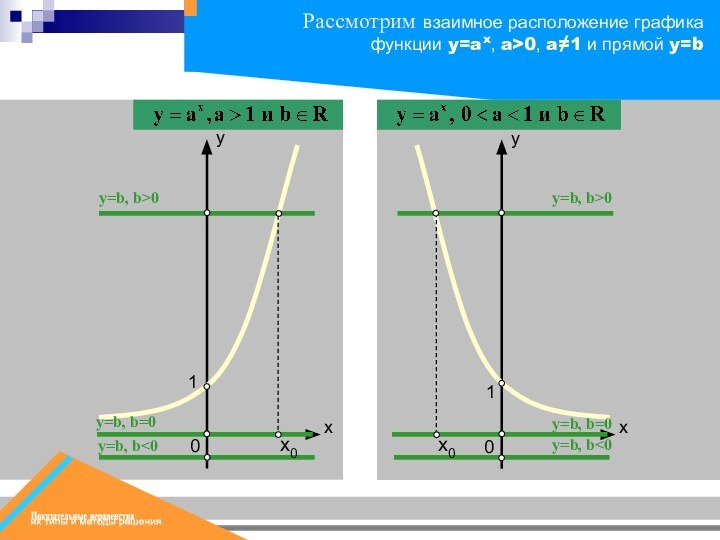
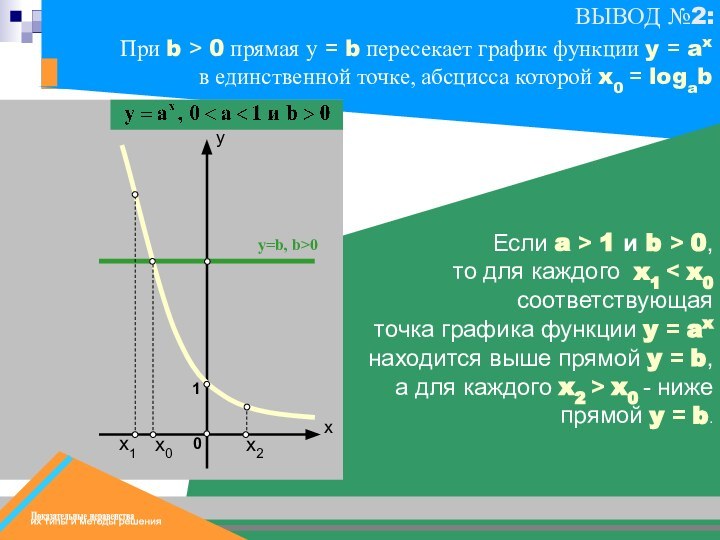
Слайд 29 х0
х1
y=b, b>0
х2
Если a > 1 и b >

х0х1y=b, b>0х2Если a > 1 и b > 0, то для

0,
то для каждого x1 < x0 соответствующая
точка

графика функции y = ax находится выше прямой y = b, а для каждого x2 > x0 - ниже прямой y = b.

При b > 0 прямая у = b пересекает график функции y = ax в единственной точке, абсцисса которой x0 = logab

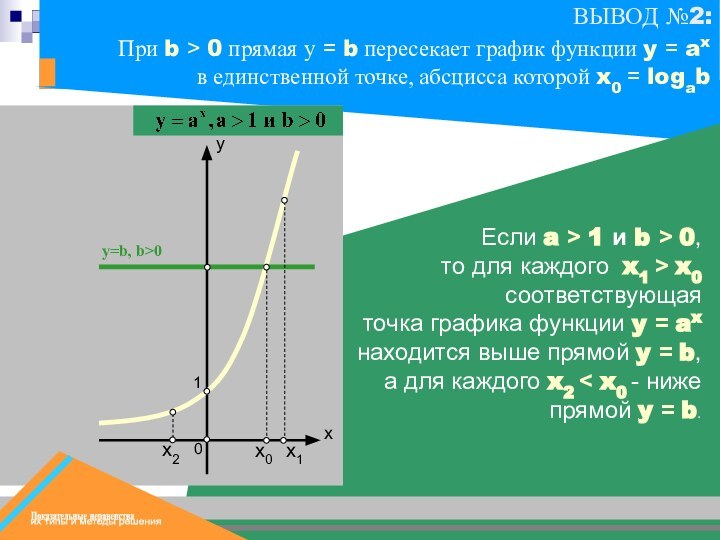
Слайд 30 х0
х1
y=b, b>0
1
Если a > 1 и b >

0,
то для каждого x1 > x0 соответствующая
точка

графика функции y = ax находится выше прямой y = b,
а для каждого x2 < x0 - ниже прямой y = b.

При b > 0 прямая у = b пересекает график функции y = ax в единственной точке, абсцисса которой x0 = logab

х2

Слайд 31

Слайд 32 возрастает на всей области определения,
Решение:

Слайд 33 Решение:
убывает на всей области определения,

Слайд 34 Решение:

возрастает на всей области определения,

Слайд 35

возрастает на всей области

определения

Слайд 36 возрастает на всей области определения,

Слайд 37 возрастает на всей области определения

Слайд 38 Вернёмся к переменной х
возрастает при всех х

из области определения

Слайд 39 возрастает на всей области определения

Слайд 40 убывает на всей
области определения

Слайд 41 Вернёмся к переменной х
убывает на всей области

определения

Слайд 42 Вернёмся к переменной х
возрастает на всей области

определения

Слайд 43 Решим каждое утверждение совокупности отдельно.

Слайд 44 Проверка
Проверка показала, что х=1, х=3, х=1,5 являются решениями

уравнения, а х=2 не является решением уравнения.

Слайд 45 Закрепление знаний
Какие неравенства называются показательными ?
Когда

Закрепление знаний Какие неравенства называются показательными ? Когда показательное неравенство имеет

показательное неравенство имеет решение при любых значениях х

?
Когда показательное неравенство не имеет решений ?
Какие типы неравенств вы узнали на этом уроке ?
Как решаются простейшие неравенства ?
Как решаются неравенства , сводящиеся к квадратным ?
Как решаются однородные неравенства ?
Как решаются неравенства , сводящиеся к рациональным ?