, sinA = cosB
2)с2 = а2 + в2
3)а = с cosβв = с sinβ
tgB = в/а
О – середина АВ ( О – центр описанной окружности)
R- радиус описанной окружности,
АВ- диаметр описанной окружности.
r- радиус вписанной окружности
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


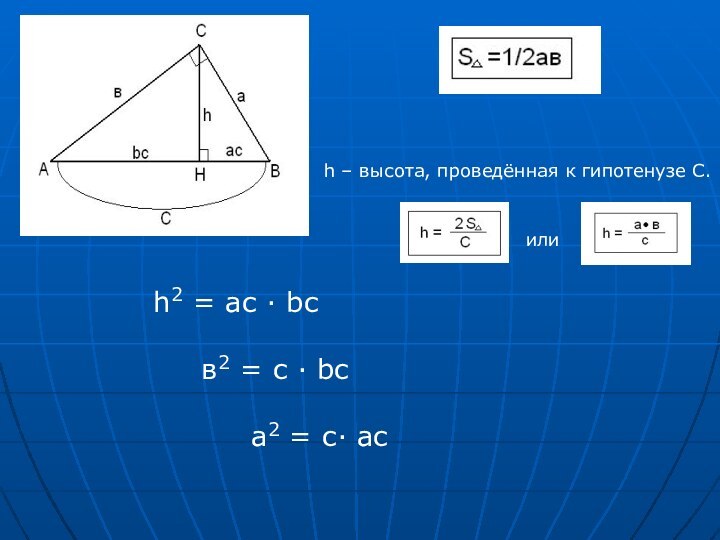







О – середина АВ ( О – центр описанной окружности)
R- радиус описанной окружности,
АВ- диаметр описанной окружности.
r- радиус вписанной окружности
Найти: S∆АВС
Решение:
1) ∆АCH: AH= 8; AC= 10; CH= √AC2 – AH2 = √102 – 82 = √36 = 6
2) CH2 = AH ∙ HB, HB= CH2/AH = 62/8 = 9/2 = 4.5
3) AB = AH + HB = 8 + 4.5 = 12.5
4) S∆= 1/2АB ∙ CH= 1/2 ∙ 6 ∙ 12.5= 37.5
Ответ. 37.5
АВ= 25, ВС= 20
О- точка пересечения медиан.
Найти: OT
Решение:
Проведём CH – высоту, тогда ОТ
OH, как перпендикуляры, проведённые к АВ.
Значит ∆ОТМ ∞ ∆ОHМ, следовательно
СМ – медиана, значит
ОМ / CM= 1/3
Тогда ОТ / CH= 1/3, т.к. CH- высота, проведённая из вершины прямого угла, то
CH= AC∙ BC / AB
AC = √AB2 – BC2 = √ 252- 202 = √225 = 15 (см)
CH= 15 ∙ 20 /25= 12 (см)
OT= CH / 3= 12/3= 4 (см)
Ответ. 4 см
P= 72см, r = 6см.
Найти: АВ
Решение:
АВ- диаметр описанной окружности. О - центр вписанной окружности ( точка пересечения биссектрис углов).
r = 6, (а + в – с)/ 2 = 6
P= а + в + с, а + в = P – c = 72 – c , тогда
(72 –с –с)/ 2= 6,
72 -2c = 12,
2c= 60,
C=30, AB= 30.
Ответ. 30 см
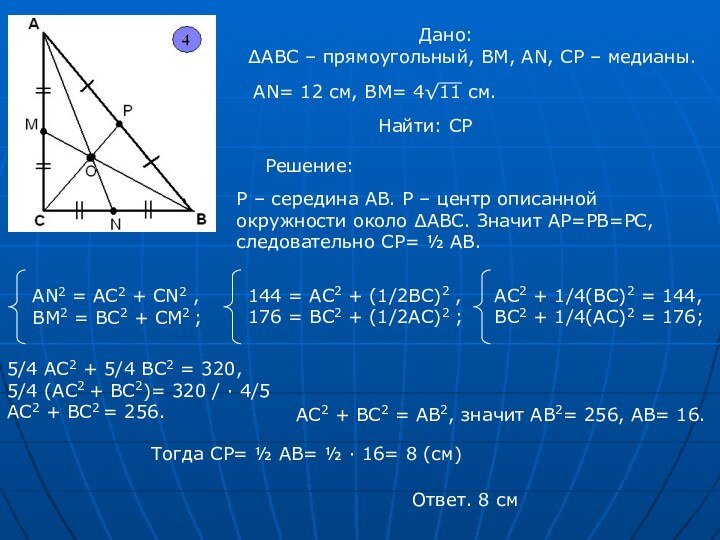
АN= 12 см, ВМ= 4√11 см.
Найти: СР
Решение:
Р – середина АВ. Р – центр описанной окружности около ∆АВС. Значит АР=РВ=РС, следовательно СР= ½ AB.
AN2 = AC2 + CN2 ,
BM2 = BC2 + CM2 ;
144 = AC2 + (1/2BC)2 ,
176 = BC2 + (1/2AC)2 ;
AC2 + 1/4(BC)2 = 144,
BC2 + 1/4(AC)2 = 176;
5/4 AC2 + 5/4 BC2 = 320,
5/4 (AC2 + BC2)= 320 / ∙ 4/5
AC2 + BC2 = 256.
AC2 + BC2 = AB2, значит AB2= 256, АВ= 16.
Тогда СР= ½ AB= ½ ∙ 16= 8 (см)
Ответ. 8 см
Найти: S∆АВС
Решение:
S∆АВС = ½ AC ∙ BC
S∆СBM = ½ MC ∙ BC , ½ MC ∙ BC = 8, MC ∙ BC = 16. (1)
sinA= 0.8, значит cosB= 0.8
tgв/2= √1- cosB / √1+ cosB= √1- 0.8 / √1+ 0.8= √0.2/1.8= √1/9= 1/3
tgв/2= MC/BC, MC/BC= 1/3, MC= 1/3 BC. (2)
Подставим в (1) равенство, получим: BC ∙ 1/3BC= 16, 1/3 BC2= 16
Значит BС2= 48, ВС= 4√3 (см)
∆АВС: BC= 4√3, sinA= 0.8
S∆АВС= ½ AC ∙ BC= ½ ∙ 3√3 ∙ 4√3= 18 (см)2
Ответ. 18 (см)2
2) В прямоугольном треугольнике АВС(∟С= 900), проведена биссектриса ВК. Найти 9√5S, где S- площадь ∆СВК. S∆ABC= 3√5, а sinA= 2/7.
Ответ. 63.
3) В прямоугольном треугольнике АВС(∟С= 900). Через центр О – вписанной в треугольник окружности проведён луч ВО, пересекающий катет АС в точке М. Известно, что АМ= 8√3, ∟А= ∟МВС. Найти гипотенузу.
Ответ. 24.