Презентация на тему Решение систем линейных уравнений

переменными?
2.Знак системы?
3.Что называют решением системы двух уравнений с двумя

двумя переменными
1.Способ подстановки
2.Способ алгебраического сложения
3.Графический способ
4.Формулы Крамера
5.Метод подбора

какого)выразить одну переменную через другую, например, y через x.
2.Полученное

(-3)
X=1
y=4-2*1
y=2
Ответ: (1;2)
2x+y=4

y=4-2x

X+2*(4-2x)=5

X+8-4x=5

X-4x=5-8

переменных;
2.Складывая или вычитая полученные уравнения, найти значение одной переменной;
3.Подставить

системы
2.Построить графики функций
в одной координатной

имеют общих точек
Одно решение,т.к. прямые пересекаются.

система уравнений не имеет решений, то она называется

x=1, y=2.

вспомогательные определители
∆ =
a1 b1
a2

=a1*b2 –a2*b1

=

C1 b1
C2 b2

=c1*b2 –c2*b1

=

A1 c1
A2 c2

=a1*c2 –a2*с1

x

x

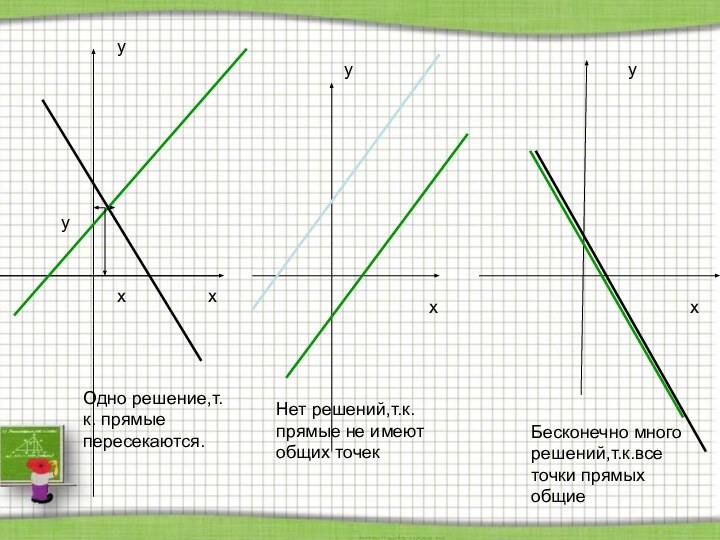
1.Если главный определитель не равен нулю, то система имеет одно решение.
2.Если главный определитель равен нулю, то:
Нет решений, если вспомогательные определители не равны нулю;
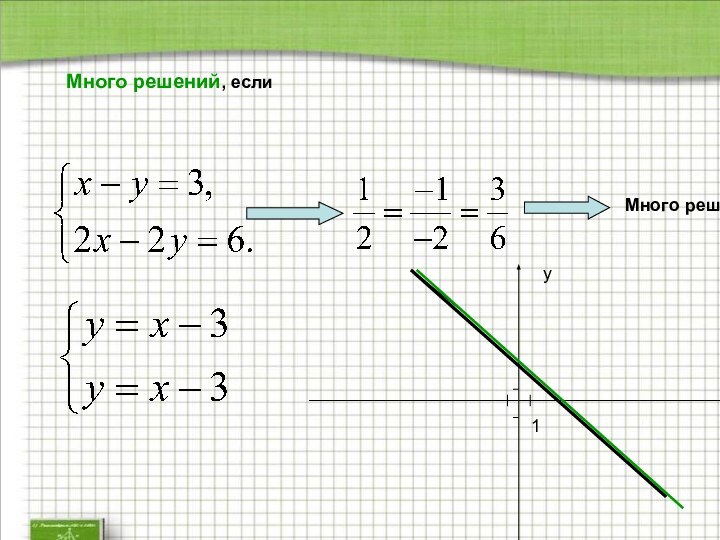
Много решений, если вспомогательные определители равны нулю

2
4 1
=5*1-4*2=-3
1 5
2 4
=1*4-2*5=-6
=-3 ;

-6 : (-3) =2

Ответ: (1;2)

2.К уравнению x+y=6 добавь

решение
Одно решение

параметра система уравнений имеет одно решение?
При каком значении параметра

решений?
Решение:
Система имеет много решений, если
4a-4=3a; 4a-3a=4; a=4
Значит при a=4

и

Так как

То при a=4 система имеет много решений

виду системы отвечать на вопрос: «сколько решений имеет система»
3.А

систему разными способами(3балла за каждый способ)




2.Решить систему уравнений методом

определите число решений системы (3балла):


4.При каком значении

5.При каком значении параметра a система не совместна ( 2 балла):