«Решение систем неравенств»
Цель
В ходе изучения темы учащиеся должны знать,что множество решений системы неравенств есть пересечение множеств решений неравенств, входящих в эту систему
2) Научить решать системы, составленные из двух линейных неравенств.



![РЕШЕНИЕ СИСТЕМ НЕРАВЕНСТВ Повторениеа≤х ≤ в,называется отрезкоми обозначается[а ; в]Если а < в, то множество чисел х, удовлетворяющих неравенствама](/img/tmb/11/1040181/09181abd7743fcfee5aa2c7b08772472-720x.jpg)
![РЕШЕНИЕ СИСТЕМ НЕРАВЕНСТВ Числовые промежуткиОтрезки[ a; в]Интервалы(а ; в)Полуинтервалы[ a; в) или ( а; в]ПовторениеЛучих>а или х< в](/img/tmb/11/1040181/c556a56477f7600a0ac2174db5b21eb4-720x.jpg)

![РЕШЕНИЕ СИСТЕМ НЕРАВЕНСТВ Проверь себя[3;6], [1,5;5]](/img/tmb/11/1040181/cc06abf5b5584fa1046ec6c1e3ae3aac-720x.jpg)
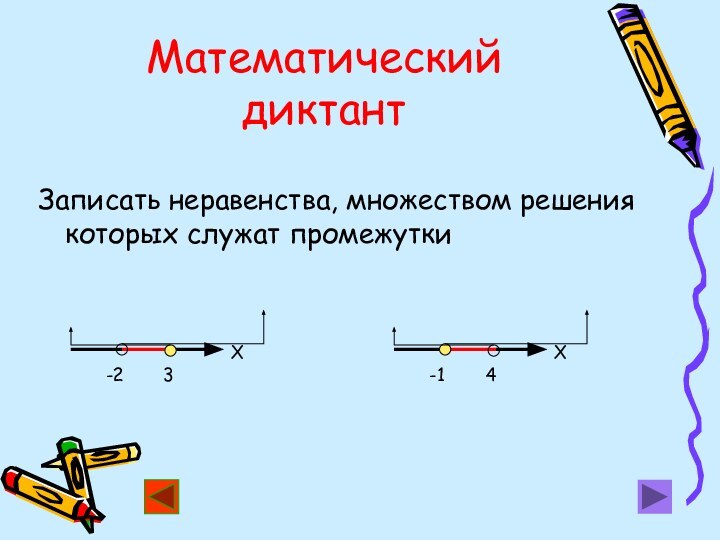
![РЕШЕНИЕ СИСТЕМ НЕРАВЕНСТВ Математический диктантКакие из целых чисел принадлежат промежутку (-1; 3,6], [-6,6;1)?](/img/tmb/11/1040181/6dcf688426204a48da88e55138ae79b9-720x.jpg)