- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Тетраэдр и пирамида
Содержание
- 2. Тетраэдр – это многогранник с четырьмя
- 3. Свойства тетраэдра
- 4. Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед(призма)
- 5. Медиан и его вершины Отрезок, соединяющий вершину
- 6. Тетраэдры в технике
- 7. Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр,
- 8. Прямоугольный тетраэдр используется в оптике. Если грани,
- 9. Вот так выглядит правильный тетраэдр
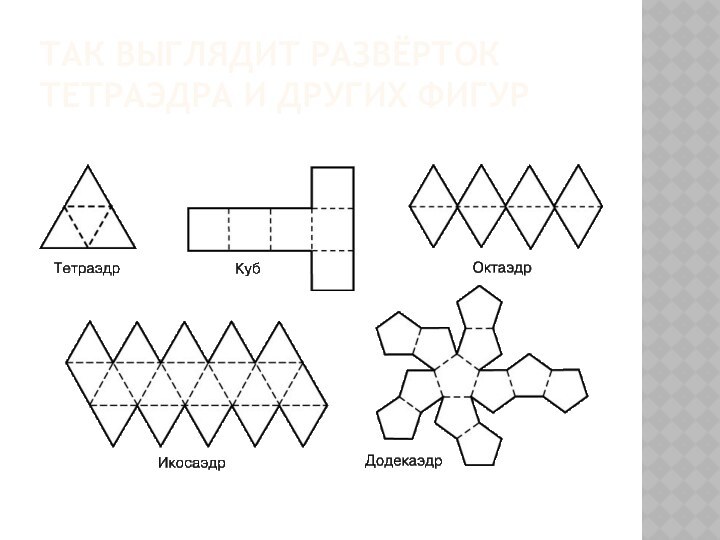
- 12. Так выглядит развёрток тетраэдра и других фигур
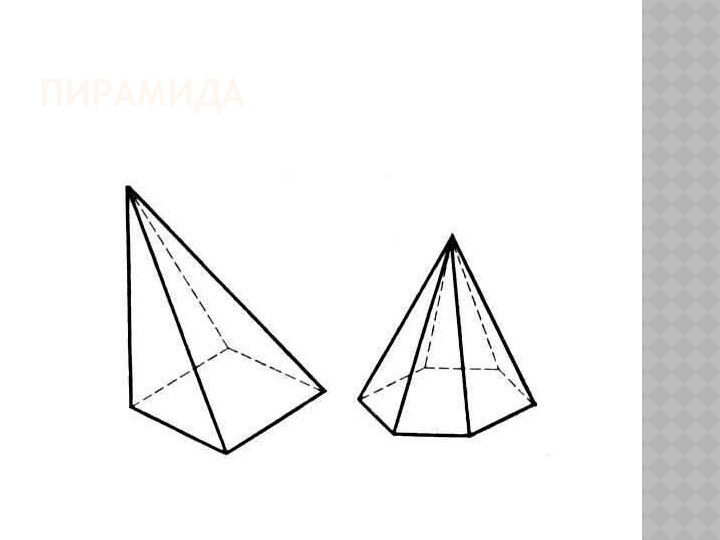
- 13. Пирамида
- 14. Пирамида , многогранник, одной из граней которого
- 15. История развития геометрии пирамиды
- 16. Начало геометрии пирамиды было положено в Древнем
- 17. Свойства пирамиды
- 18. Все диагонали пирамиды принадлежат её граням.Если все
- 19. Если боковые грани наклонены к плоскости основания
- 20. Так выглядит развёрток пирамиды
- 21. Скачать презентацию
- 22. Похожие презентации
Тетраэдр – это многогранник с четырьмя треугольными гранями, в каждой из вершин которого сходятся по 3 грани. У тетраэдра 4 грани, 4 вершины и 6 рёбер.



















Слайд 4 Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра,
определяют описанный около тетраэдра параллелепипед(призма)
Слайд 5
Медиан и его вершины
Отрезок, соединяющий вершину тетраэдра
с точкой пересечения медиан противоположной грани, называется его медианой,
опущенной из данной вершины.Слайд 7 Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный
из стержней, часто используется в качестве основы для пространственных
несущих конструкций пролётов зданий, перекрытий, балок, ферм мостов и т.д. Стержни испытывают только продольные нагрузки.Слайд 8 Прямоугольный тетраэдр используется в оптике. Если грани, имеющие
прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить
из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.Слайд 14 Пирамида , многогранник, одной из граней которого служит
многоугольник, а остальные грани суть треугольники с общей вершиной
. В зависимости от числа боковых граней П. делятся на треугольные, четырёхугольные и т.д.Слайд 16 Начало геометрии пирамиды было положено в Древнем Египте
и Вавилоне, однако активное развитие получило в Древней Греции.
Первый, кто установил, чему равен объем пирамиды, был Демократ [2], а доказал Евдокс Книдский. Древнегреческий математик Евклид, систематизировал знания о пирамиде в XII томе своих «Начал», а также вывел первое определение пирамиды: телесная фигура, ограниченная плоскостями, которые от одной плоскости сходятся в одной точке.
Слайд 18
Все диагонали пирамиды принадлежат её граням.
Если все боковые
ребра равны, то:
около основания пирамиды можно описать окружность, причём
вершина пирамиды проецируется в её центр;боковые ребра образуют с плоскостью основания равные углы.
Слайд 19 Если боковые грани наклонены к плоскости основания под
одним углом, то:
в основание пирамиды можно вписать окружность, причём
вершина пирамиды проецируется в её центр;высоты боковых граней равны;
площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани.