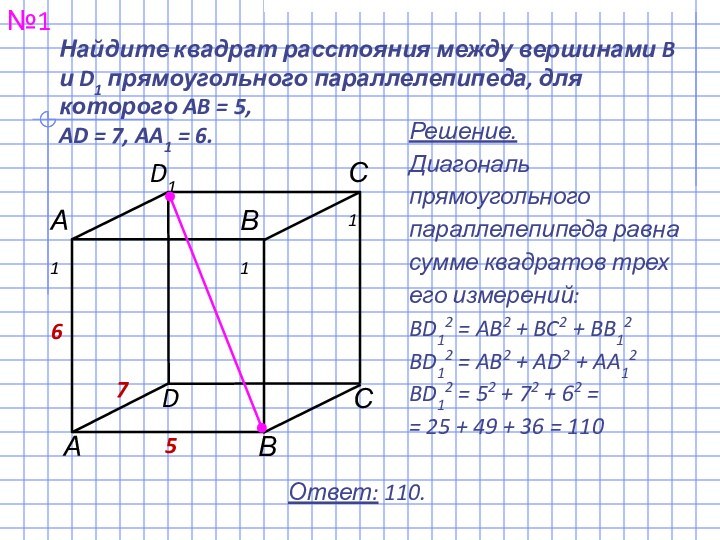
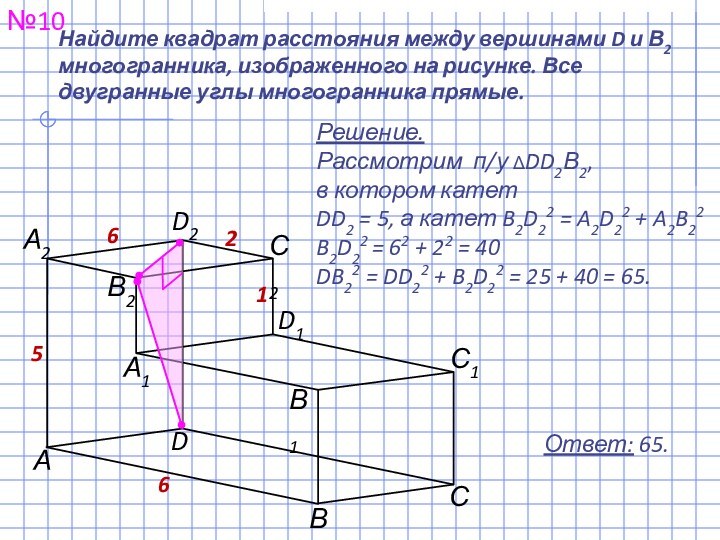
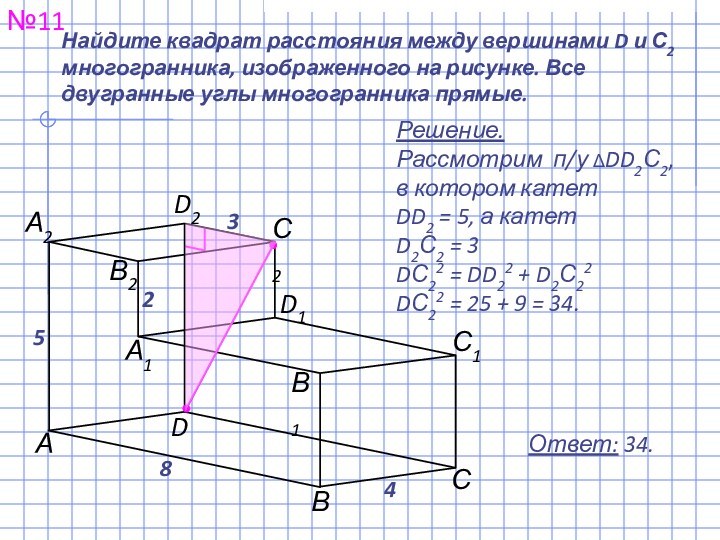
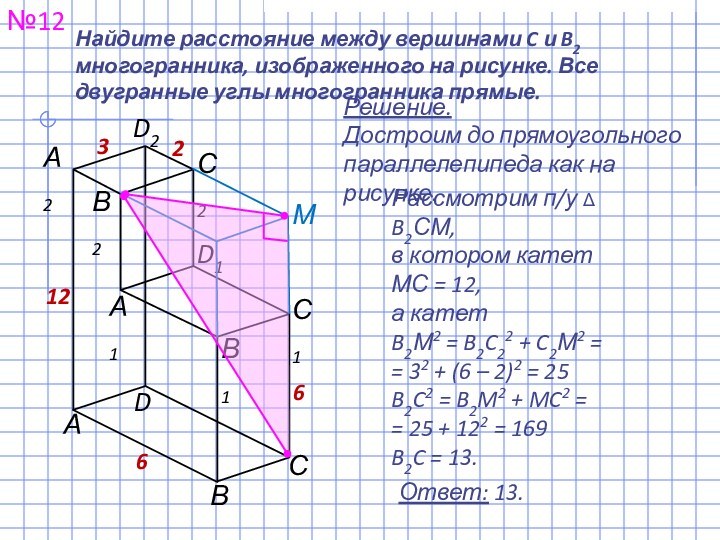
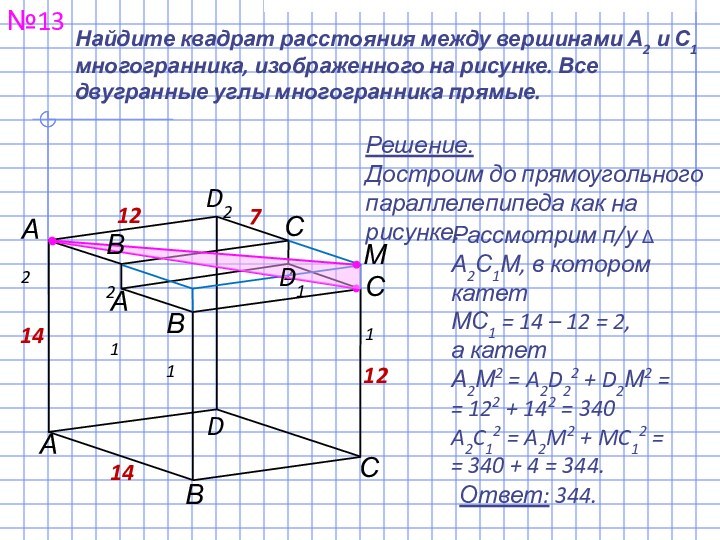
прямоугольного параллелепипеда, для которого AB = 5,
AD =
7, AA1 = 6.№1
Решение.
Диагональ прямоугольного параллелепипеда равна сумме квадратов трех его измерений:
BD12 = AB2 + BC2 + BB12
BD12 = AB2 + AD2 + AA12
BD12 = 52 + 72 + 62 =
= 25 + 49 + 36 = 110
Ответ: 110.