Слайд 2
Показать свои знания основного теоретического материала по темам
«Аксиомы стереометрии», «Параллельность прямой и плоскости», «Параллельность плоскостей», «Перпендикулярность
прямой и плоскости»;
Научиться работать с инструментами: вставка объекта и надписи, прямые, тип линий, тип штриха, цвет линий, эллипс, группировка объектов, эффекты и настройка анимации, управляющие кнопки, WordArt;
Развитие способности практического применения основных теорем и аксиом стереометрии при построении сечений;
научиться планировать свою деятельность.
Цели:
Слайд 3
Содержание:
Список применяемых теорем
Проектное задание №1
Проектное задание №2
Проектное задание
№3
Проектное задание №4
Проектное задание №5
Проектное задание №6
Проектное
задание №7
Проектное задание №8
Проектное задание №9
Мои инструменты
Выводы
Слайд 4
Сводный список применявшихся теорем:
С2: Если две различные плоскости

имеют общую точку, то они пересекаются по прямой, проходящей
через эту точку.
С3: Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
Теорема 15.1 : Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.
Теорема 15.2 : Если две точки прямой принадлежат этой плоскости, то вся прямая принадлежит этой плоскости.
Теорема 15.3 : Через три точки ,не лежащие на одной прямой, можно провести плоскость, и притом только одну.
Теорема 16.1 : Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну.
Теорема 16.2 : Две прямые, параллельные третьей прямой, параллейны.
Теорема 16.3 : Если прямая, не принадлежащая плоскости, параллельна какой-ни будь прямой в этой плоскости, то она параллельна и самой плоскости.
Свойство параллельных плоскостей: Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллейны.
Свойство перпендикулярных прямой и плоскости: Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Признак перпендикулярности прямой и плоскости: Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости.
Слайд 5
Решение:
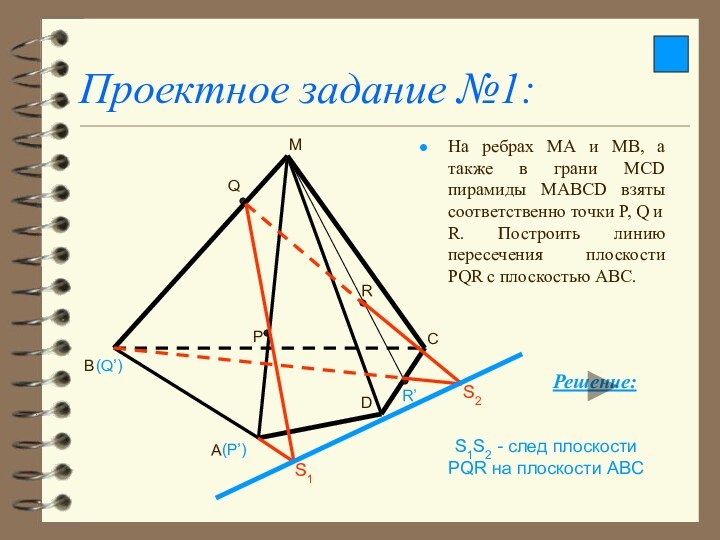
Проектное задание №1:
На ребрах МА и МВ, а
также в грани МСD пирамиды МАВСD взяты соответственно точки
P, Q и R. Построить линию пересечения плоскости PQR с плоскостью АВС.
S1S2 - след плоскости PQR на плоскости ABC
Слайд 6
Решение:
Построим точки Р’, Q’, R’ - проекции соответственно
точек P, Q, R на плоскость АВС.
Прямые PQ и
P’Q’ лежат в одной плоскости. Найдем точку S1, в которой пересекаются эти прямые. По теореме 15.2. точка S1 является общей точкой плоскостей PQR и АВС. По аксиоме С2 эти плоскости пересекаются по прямой, проходящей через точку S1 .
Аналогично найдем точку S2 , в которой пересекаются прямые QR и Q’R’ и которая является общей для плоскостей PQR и АВС. По аксиоме С2 эти плоскости пересекаются по прямой, проходящей через точку S2 .
Проведём прямую S1 S2. По теореме 15.2. Эта прямая лежит как в плоскости АВС, так и в плоскости PQR. Таким образом, прямая S1 S2 -это искомая линия пересечения.
Линию пересечения двух плоскостей называют также следом одной из них на другой.
Слайд 7
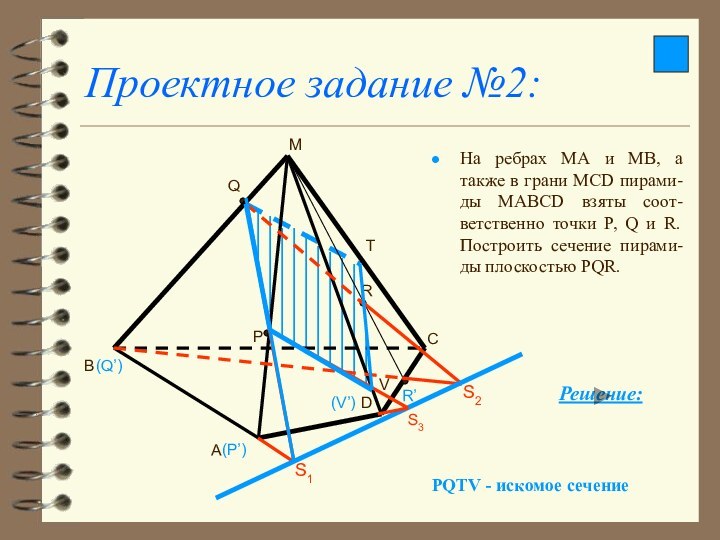
Проектное задание №2:
На ребрах МА и МВ, а
также в грани МСD пирами-ды МАВСD взяты соот-ветственно точки
P, Q и R. Построить сечение пирами-ды плоскостью PQR.
(V’)
PQTV - искомое сечение
Решение:
Слайд 8
Решение:
Построим прямую S1S2- след плоскости PQR на плоскости

АВС.
Линия пересечения плоскости PQR с плоскостью МАВ - прямая
QS1, а отрезок QP - это пересечение плоскости PQR с гранью МАВ.
Точка Р является общей точкой плоскостей PQR и МАD. Эти плоскости пересекаются по прямой, проходящей через точку Р (по Т 15.2.). Проекция точки пересечения прямой МD с плоскостью PQR на плоскость АВС совпадает с точкой D. Пересечение Р’V’ с прямой S1S2 дает точку S3. Точка S3 является общей точкой плоскостей PQR и МАD. Эти плоскости пересекаются по прямой, проходящей через точку S3 (по Т 15.2.).
Точки Р и S3 являются общими для плоскостей PQR и МАD. Значит, прямая РS3 - это линия пересечения этих плоскостей. Проведем её и найдём точку V, в которой прямая РS3 пересекает MD. Отрезок PV является пересечением плоскости PQR с гранью МАD.
Точки R и V являются общими для плоскостей PQR и МCD. Значит, прямая RV - это линия пересечения этих плоскостей. Найдём точку T, в которой прямая RV пересекает MC. Отрезок VT является пересечением плоскости PQR с гранью МCD.
Отрезок QT - это пересечение плоскости PQR с гранью MBC
PQTV - искомое сечение
Слайд 9
Решение:
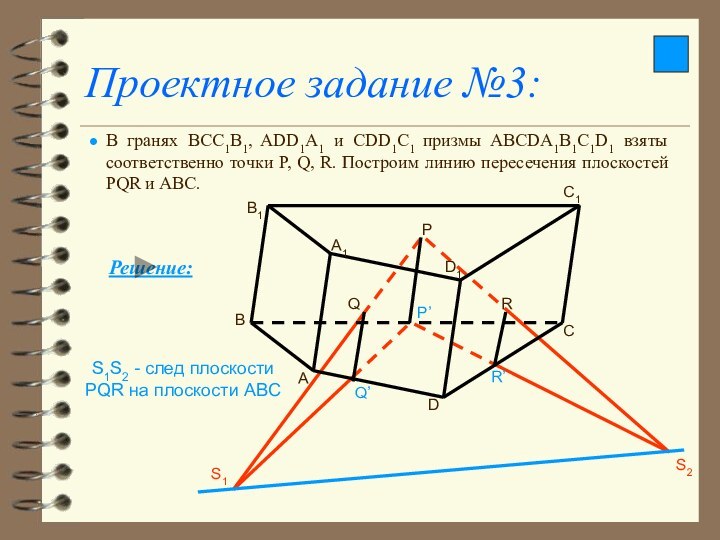
Проектное задание №3:
В гранях BCC1B1, ADD1A1 и CDD1C1
призмы ABCDA1B1C1D1 взяты соответственно точки P, Q, R. Построим
линию пересечения плоскостей PQR и АВС.
S1S2 - след плоскости PQR на плоскости ABC
Слайд 10
Решение:
Построим точки Р’, Q’, R’ - проекции соответственно
точек P, Q, R на плоскость АВС.
Так как ВВ1||АА1
, ВВ1||РР’ , АА1||QQ’, то РР’ ||QQ’ и, значит, определя-ют плоскость. Прямые PQ и P’Q’ лежат в одной плоскости. Найдем точку S1, в которой пересекаются эти прямые. По теореме 15.2. точка S1 является общей точкой плоскостей PQR и АВС. По аксиоме С2 эти плоскости пересекаются по прямой, проходящей через точку S1 .
Так как CC1||РР’ , CC1||RR’, то РР’ ||RR’ и, значит, определяют плоскость. Аналогично найдем точку S2 , в которой пересекаются прямые QR и Q’R’ и которая является общей для плоскостей PQR и АВС. По аксиоме С2 эти плоскости пересекаются по прямой, проходящей через точку S2 .
Проведём прямую S1 S2. По теореме 15.2. Эта прямая лежит как в плоскости АВС, так и в плоскости PQR. Таким образом, прямая S1 S2 -это искомая линия пересечения.
Слайд 11
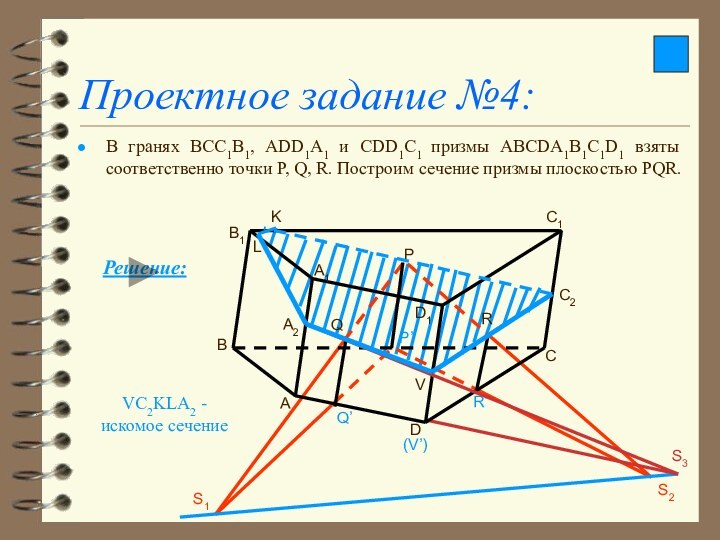
Проектное задание №4:
В гранях BCC1B1, ADD1A1 и CDD1C1
призмы ABCDA1B1C1D1 взяты соответственно точки P, Q, R. Построим
сечение призмы плоскостью PQR.
(V’)
VC2KLA2 - искомое сечение
Решение:
Слайд 12
Решение:
Построим прямую S1S2- след плоскости PQR на плоскости

АВС.
Точка Q является общей для плоскостей PQR и АDD1.
Они пересекаются по прямой, проходящей через точку Q (по Т 15.2.). Проекция точки пересечения прямой DD1 с плоскостью PQR на плоскость АВС совпадает с точкой D. Пересечение Q’V’ с пря-мой S1S2 дает точку S3. Точка S3 является общей для плоскостей PQR и АDD1. Эти плоскости пересекаются по прямой, проходящей через точку S3 (по Т 15.2.).
Точки Q и S3 являются общими для плоскостей PQR и АDD1. Значит, прямая QS3 - это линия пересечения этих плоскостей. Проведем её и найдём точки V(точка пере-сечения прямых QS3 и DD1) и А2(точка пересечения прямых QS3 и АА1). Отрезок А2V является пересечением плоскости PQR с гранью АDD1A1.
Точки R и V являются общими для плоскостей PQR и C1CD. Значит, прямая RV - это линия пересечения этих плоскостей. Найдём точку C2 , в которой прямая RV пе-ресекает CC1. Отрезок VC2 является пересечением плоскости PQR с гранью C1CDD1.
Рассуждая аналогично найдем отрезок С2К, который является пересечением плоскости PQR с гранью C1CВB1.
По свойству параллельных плоскостей прямые S1S2||KL, где К - это точка пересе-чения ребра В1А1 с плоскостью PQR.
VC2KLA2 - искомое сечение
Слайд 13
Решение:
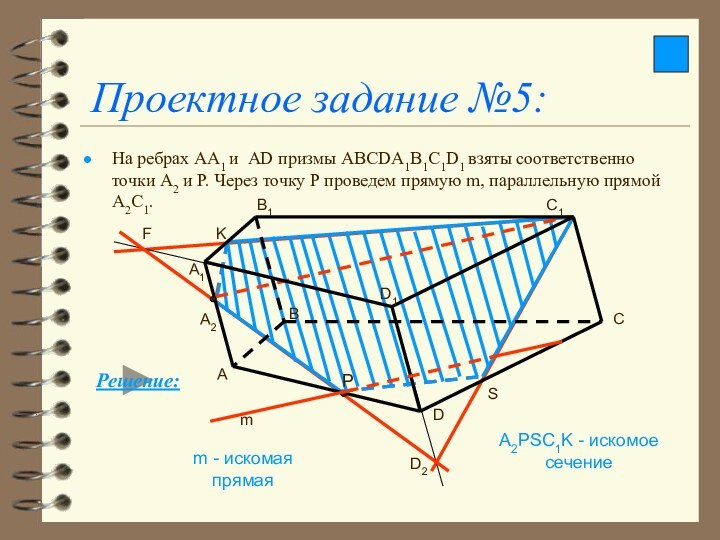
Проектное задание №5:
На ребрах АА1 и АD призмы
ABCDA1B1C1D1 взяты соответственно точки А2 и Р. Через точку
Р проведем прямую m, параллельную прямой А2С1.
A2PSC1K - искомое сечение
m - искомая прямая
Слайд 14
Решение:
Проведём прямую А2Р и найдем точки пересечения А2Р
с DD1 и A1D1 (D2 и F соответственно).
Проведем прямую
D2C1 и найдем S - точку пересечения прямых D2C1 и CD.
Проведём прямую SP.
Проведём прямую C1F и найдём К - точку пересечения C1F и А1В1. .
Соединим точку А2 с точкой К
А2PSC1K- сечение призмы
В плоскости А2С1Р через точку Р проведем прямую m||А2С1 и найдем Y -точка пересечение прямых m и D2C1.
PY-искомая прямая
Замечание: Прямые PS и KC1 получились параллельными. Закономерность этого факта обосновывается свойством параллельных плоскостей АВС и А1В1С1.
Слайд 15
Решение:
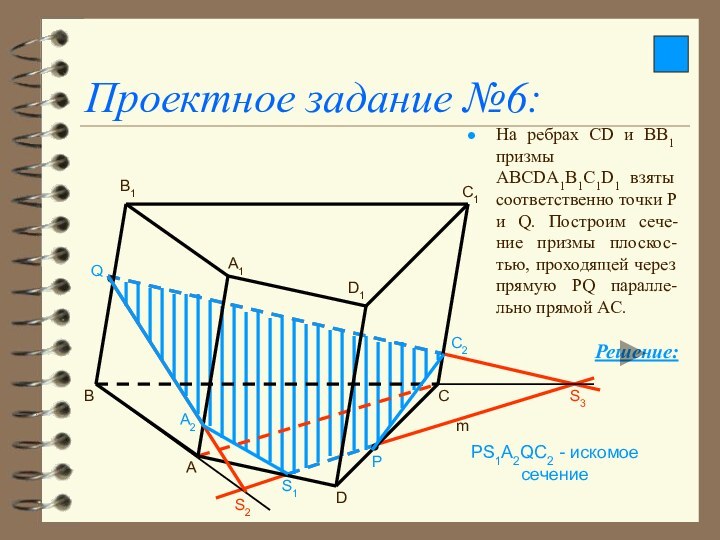
Проектное задание №6:
На ребрах СD и ВВ1 призмы
ABCDA1B1C1D1 взяты соответственно точки P и Q. Построим сече-ние
призмы плоскос-тью, проходящей через прямую PQ паралле-льно прямой АС.
PS1A2QC2 - искомое сечение
Слайд 16
Решение:
В плоскости АВС проведём прямую m||АС.
Найдем S1, S2,
S3 - точки пересечения прямой m с прямыми AD,
AB, BC соответственно.
Прямая QS2 - линия пересечения секущей плоскости с плоскостью АВВ1. Найдем А2 - точку пересечения прямых АА1 и QS2. Отрезок QА2 является пересечением секущей плоскости с гранью АВВ1А1.
Прямая QS3 - линия пересечения секущей плоскости с плоскостью ВСС1. Найдем С2 - точку пересечения прямых СС1 и QS3. Отрезок QС2 является пересечением секущей плоскости с гранью ВСС1С1.
Соединим точку А2 с точкой S1 и точку С2 с точкой Р. Отрезки А2S1 и С2Р являются пересечениями секущей плоскости соответственно с гранями АDD1A1 и CDD1C1.
PS1A2QC2 - искомое сечение
Слайд 17
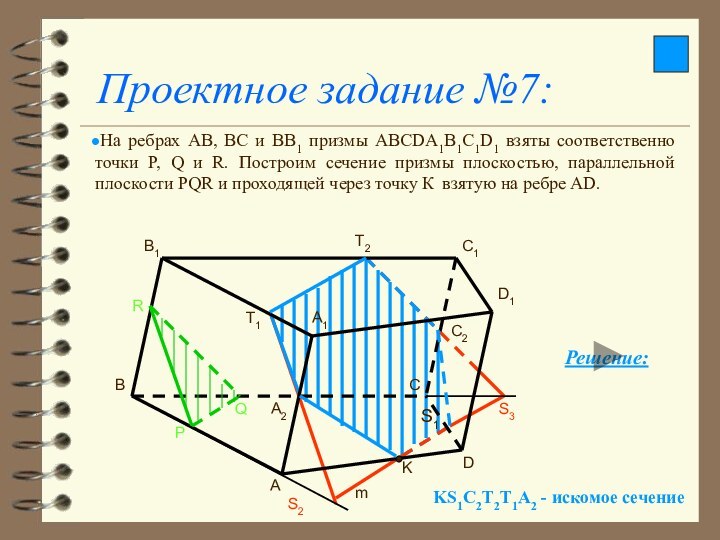
Проектное задание №7:
На ребрах АВ, ВС и ВВ1
призмы ABCDA1B1C1D1 взяты соответственно точки P, Q и R.
Построим сечение призмы плоскостью, параллельной плоскости PQR и проходящей через точку К взятую на ребре АD.
KS1C2T2T1A2 - искомое сечение
Решение:
Слайд 18
Решение:
В плоскости АВС через точку К проведём прямую
m||PQ.
Найдем S1, S2, S3 - точки пересечения прямой m
с прямыми СD, AB, BC соответственно.
В плоскости АВВ1 через точку S2 прямую n||PR.
Найдем А2, Т1 - точки пересечения прямой n с прямыми AА1, B1А1 соответственно.
В плоскости СВВ1 через точку S3 прямую k||QR.
Найдем C2, Т2 - точки пересечения прямой k с прямыми CC1, B1C1 соответственно.
Соединим точку Т1 с точкой Т2, точку S1 с точкойC2, точку A2 с точкой K.
KS1C2T2T1A2 - искомое сечение
Замечание: Прямые КS1 и Т1Т2 получились параллельными. Закономерность этого факта обосновывается свойством параллельных плоскостей АВС и А1В1С1.
Слайд 19
Решение:
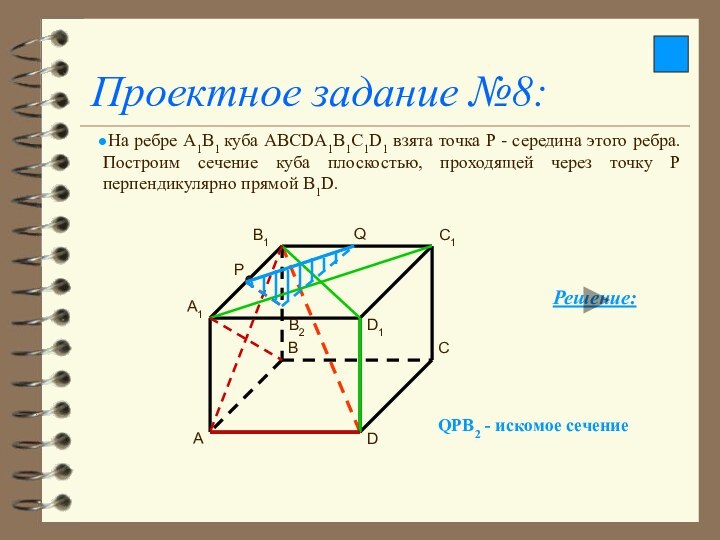
Проектное задание №8:
На ребре А1В1 куба ABCDA1B1C1D1 взята
точка Р - середина этого ребра. Построим сечение куба
плоскостью, проходящей через точку Р перпендикулярно прямой В1D.
QPB2 - искомое сечение
Слайд 20
Решение:
Так как А1С1 перпендикулярна В1D1 и А1С1 перпендикулярна
DD1, то по признаку перпендикулярности прямой и плоскости прямая
А1С1 перпендикулярна плоскости DD1В1.
Проведём в плоскости А1В1С1 через точку Р прямую PQ||А1С1. По свойству перпендикулярных прямой и плоскости прямая PQ перпендикулярна плоскости DD1В1, и, следовательно, она перпендикулярна любой прямой, лежащей в этой плоскости. В частности, PQ перпендикулярна В1D.
Рассуждая аналогично, проведём через точку Р в плоскости АВВ1 прямую РВ2||А1В. Тогда РВ2 перпендикулярна В1D.
Так как прямая В1D ( по построению) перпендикулярна двум пересекающимся прямым PQ и РВ2, то плоскость, определяемая этими прямимы, перпендикулярна прямой В1D.
QPB2 - искомое сечение
Слайд 21
Решение:
Проектное задание №9:
Высота МО правильной пирамиды МАВСD равна
стороне ее основания. По-строим сечение пирамиды плоскостью, проходящей через
вершину D перпенди-кулярно прямой МВ.
DA1HC1 - искомое сечение
Слайд 22
Решение:
В плоскости BMD опустим перпендикуляр из точки D
на прямую МВ. Выполним это построение вычислительным способом. Для
построения точки Н подсчитаем, что отношение ВН:ВМ=2:3. Зная это отношение параллельных отрезков ВН и ВМ, построим с помощью вспомогательного луча m точку Н и проведем затем прямую DH.
Проведем в плоскости МАС через точку пересечения прямых DH и МО прямую А1С1||АС. По свойству перпендикулярных прямой и плоскости АС перпендикулярна плоскости BDM. Следовательно, она перпендикулярна любой прямой, лежащей в этой плоскости. В частности, А1С1 перпендикулярна МВ.
Пересекающимися прямыми А1С1 и DH определяется плоскость, проходящая через точку D перпендикулярно прямой МВ.
DA1HC1 - искомое сечение
Слайд 23
При выполнении данного проекта мою деятельность мож-но разделить
на три этапа:
работа с текстом;
геометрические построения;
анимация.
При работе с текстом
я использовала: вставку надписи, цвет текста, нижний индекс, шрифт, размер шрифта.
Для геометрического построения мне были необходимы ин-струменты: линии, цвет линии, тип линии, тип штриха, овал.
Для того чтобы выполнить анимацию мне был нужен ин-струмент-группировка. Без него анимация была бы трудо-емкой.
Я старалась выдержать проект в едином стиле.
МОИ ИНСТРУМЕНТЫ: