Презентация на тему Сечения тетраэдра

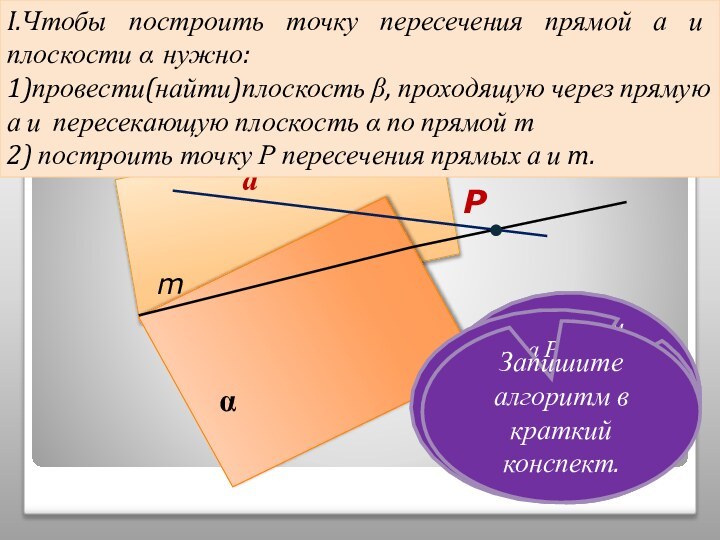
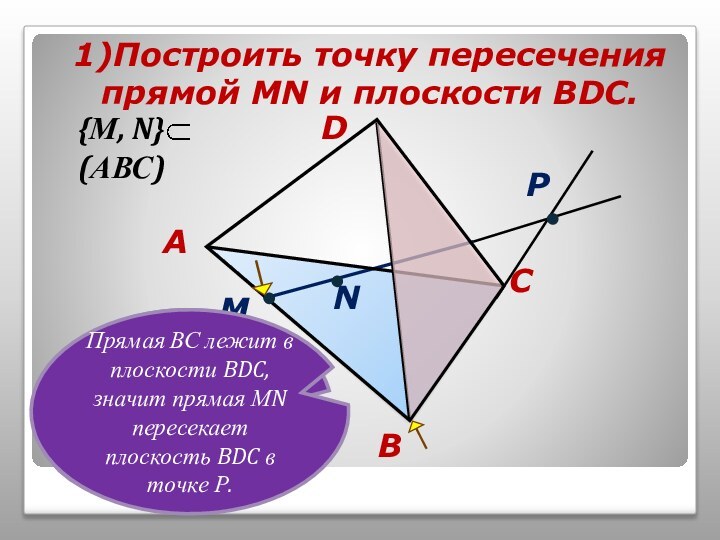
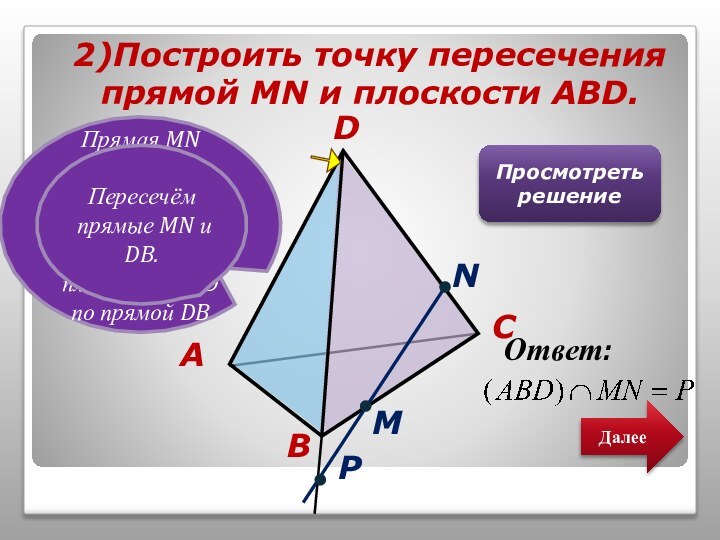
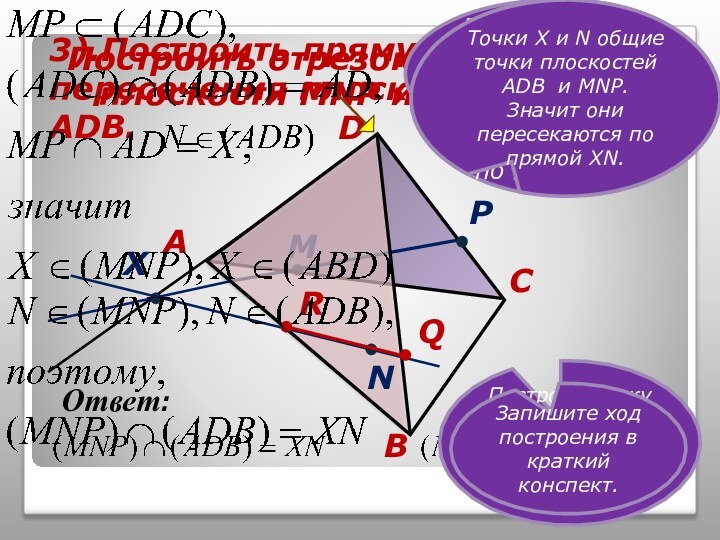
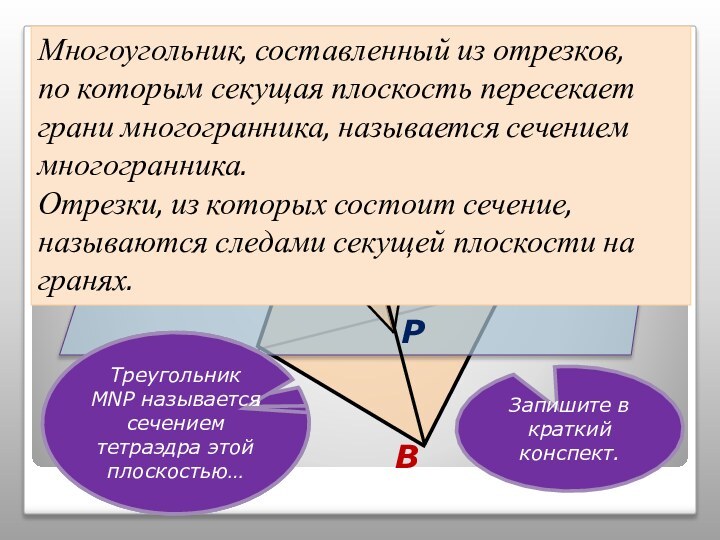
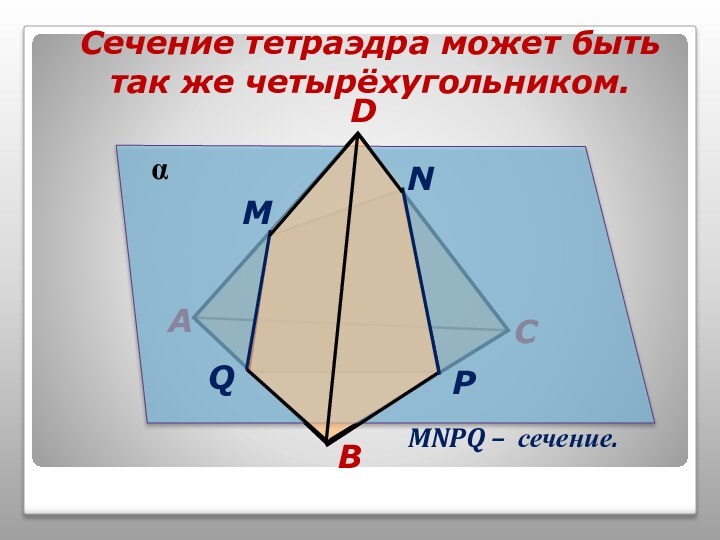
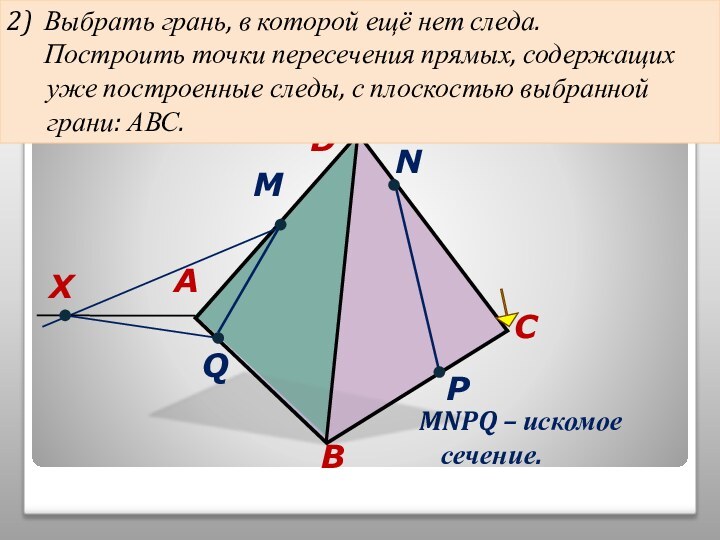
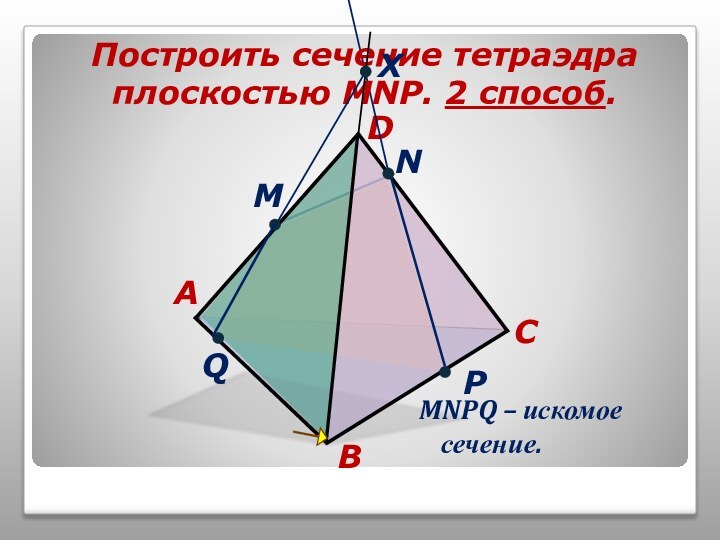
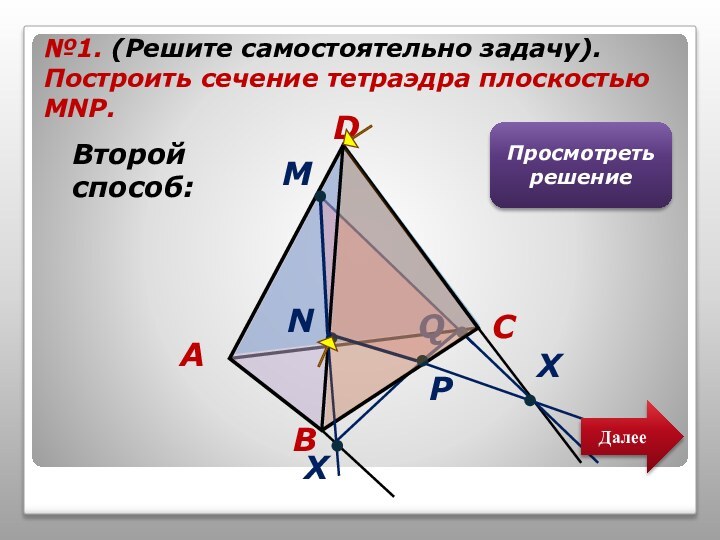
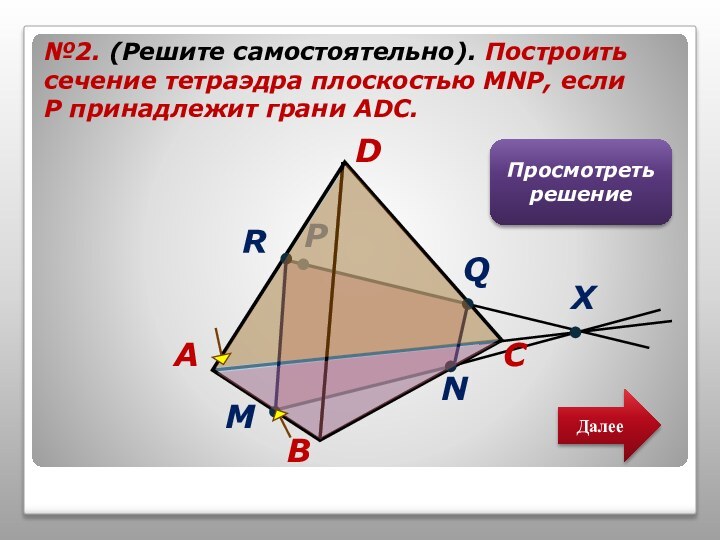
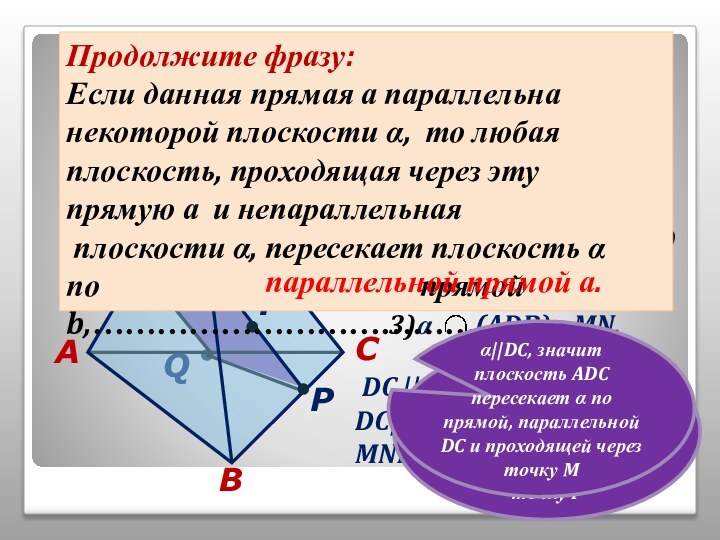
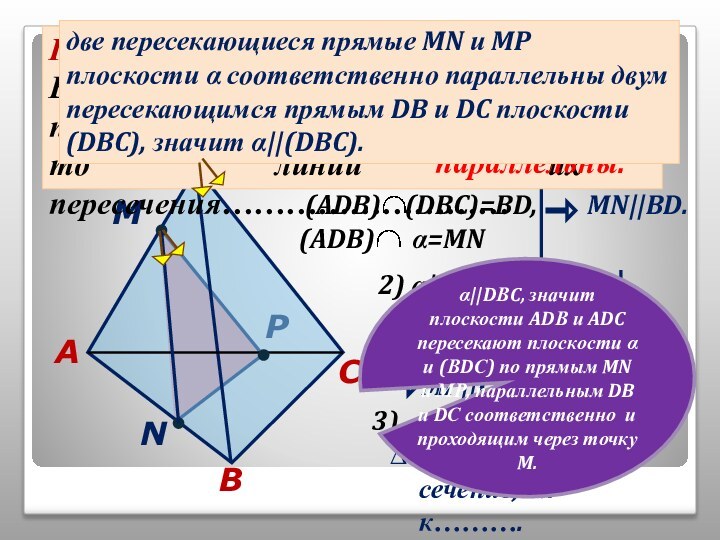
том, чтобы наглядно продемонстрировать алгоритмы построения точки пересечения прямой

и плоскости, прямой пересечения плоскостей и сечений тетраэдра.
Учитель может использовать презентацию при проведении уроков по этой теме, или рекомендовать её для самостоятельного изучения учащимся, пропустившим по какой-то причине её изучение, или для повторения ими отдельных вопросов.
Ученики сопровождают изучение презентации заполнением краткого конспекта.

том, чтобы наглядно продемонстрировать алгоритмы решения задач на построение

в пространстве.
Постарайтесь внимательно и, не спеша, изучать комментарии на выносках и сопоставлять их с рисунком.
Заполняйте в кратком конспекте все пропуски.
При самостоятельном решении задач необходимо вначале самому продумать решение, а затем просмотреть предложенное автором.
Запишите вопросы к учителю и задайте их на уроке.

построить точку пересечения прямой а и плоскости α нужно:
1)провести(найти)плоскость

β, проходящую через прямую а и пересекающую плоскость α по прямой т
2) построить точку Р пересечения прямых а и m.

Через прямую а проведём плоскость β, пересекающую плоскость α по прямой т

Пересечём прямую а с линией пересечения плоскостей α и β: прямой т.

Точка Р общая точка прямой а и плоскости α, т.к. прямая т лежит в плоскости α.

Запишите алгоритм в краткий конспект.

N} (АВС)
Ответ:


Через прямую МN проходит плоскость АВС,

пересекающая плоскость BDC по прямой ВС.

Прямая МN пересекается с прямой ВС в точке Р.

Прямая ВС лежит в плоскости BDC, значит прямая МN пересекает плоскость BDC в точке Р.

решение
Прямая MN принадлежит плоскости ВDC, которая пересекает плоскость AВD

по прямой DB

Пересечём прямые MN и DB.

Далее

По условию и построению
точки С и Р общие для

плоскостей АВС и α.

По условию и построению
точки С и Р общие для плоскостей АВС и α.

Значит прямая СР искомая прямая пересечения плоскостей
АВС и α.

II. Пусть прямая АВ не параллельна плоскости α . Построить линию пересечения плоскостей α и АВС, если точка С принадлежит плоскости α

II.Чтобы построить линию пересечения
плоскости α и плоскости АВС
(С α, {А, В} α, АВ || α), нужно:
построить точку пересечения прямой АВ
и плоскости α - точку Р ;
2) точка Р и С общие точки плоскостей (АВС)
и α, значит (АВС) α = СР

Запишите алгоритм в краткий конспект.

прямую пересечения плоскостей МNP и АDB.

D
B
A
C
N
P



X
Q
R


Ответ:

Построим точку пересечения прямой

МР с плоскостью ADB (точку Х).

Прямая МР лежит в плоскости ADС, пересекающей плоскость ADВ по прямой AD.

Прямая МР лежит в плоскости ADС, пересекающей плоскость ADВ по прямой AD.

Точки Х и N общие точки плоскостей ADВ и MNP. Значит они пересекаются по прямой ХN.

Запишите ход построения в краткий конспект.

плоскость пересекает
грани многогранника, называется сечением
многогранника.
Отрезки, из которых

состоит сечение,
называются следами секущей плоскости на
гранях.

∆ MNP – сечение.

Пусть плоскость пересекает тетраэдр, тогда она называется секущей плоскостью

Плоскость пересекает рёбра тетраэдра в точках М,N,P, а грани - по отрезкам MN, MP, NP…

Треугольник МNP называется сечением тетраэдра этой плоскостью…

Запишите в краткий конспект.

MNPQ – сечение.

D



Алгоритм построения сечения тетраэдра

плоскостью, проходящей через три данные точки M,N,P.

B

A

C

M

N

P

Q

X

Построить следы секущей плоскости в тех
гранях, в которых есть 2 общие точки с ней.

3)Через построенные точки провести прямую, по которой секущая плоскость пересекает
плоскость выбранной грани АВС.

4) Отметить и обозначить точки, в которых
эта прямая пересекает рёбра грани АВС и достроить остальные следы.

2) Выбрать грань, в которой ещё нет следа.
Построить точки пересечения прямых, содержащих уже построенные следы, с плоскостью выбранной грани: АВС.

– искомое сечение.

MNP.

D
A
C
M
N
P



X

B
X




Просмотреть решение
Второй
способ:
Далее

если Р принадлежит грани АDC.
D
B
A
M
N

P

C



X
Q
R






Просмотреть решение
Далее

α (ABC)=QP.

Q

№3. Построить сечение тетраэдра плоскостью α, параллельной ребру CD и проходящей через т. F, лежащую на плоскости DBC, и точку М.

D

B

A

M

N

P

F

C

Дано: α||DC, {M;F} α, F (BDC), M AD.

Построить сечение тетраэдра DABC

Т.к. α||DC, то (DBC) α=FP
и FP||DC, FP BC=P, FP BD=N.

2) Т. к. α||DC, то (DAC) α=MQ
и MQ||DC, MQ AC=Q.

DC || NP и NP α, значит
DC||α, следовательно
MNPQ – искомое сечение.

Продолжите фразу:
Если данная прямая а параллельна
некоторой плоскости α, то любая
плоскость, проходящая через эту
прямую а и непараллельная
плоскости α, пересекает плоскость α
по прямой b,………………………………………

параллельной прямой а.

Продолжите…

α||DC, значит плоскость BDC пересекает α по прямой, параллельной DC и проходящей через точку F

α||DC, значит плоскость ADC пересекает α по прямой, параллельной DC и проходящей через точку M

(ADC) α=MN
MP||CD.



P
№4.

Построить сечение тетраэдра плоскостью α, параллельной грани BDC и проходящей через точку М.

B

A

C

M

N

D

Дано: α||DBC, M α, M AD.

Построить сечение тетраэдра DABC
плоскостью α

α||DВC,
(ADB) (DBC)=BD, MN||BD.
(ADB) α=MN

3) α (ABC)=NP.

∆ MNP – искомое сечение, т.к……….

Продолжите фразу:
Если две параллельные плоскости
пересечены третьей плоскостью,
то линии их пересечения………………………

параллельны.

две пересекающиеся прямые MN и MP
плоскости α соответственно параллельны двум пересекающимся прямым DB и DC плоскости (DBC), значит α||(DBC).

α||DВC, значит плоскости ADВ и ADC пересекают плоскости α и (ВDС) по прямым MN и МР, параллельным DB и DС соответственно и проходящим через точку M.

плоскостью α, проходящей через точку М и отрезок PN,

если PN||AB и М принадлежит плоскости (АВС).

Р

Q

D

1) NP||АВ NP||(ABC)
NP α,
α (ABC) =MQ
MQ||NP.

2)MQ AC=R.
α (ADC)=NR,
α (BDC)=PQ.
RNPQ-искомое сечение.

Просмотреть решение

NP||(AВC), значит плоскость MNP пересекает плоскость AВС по прямой MQ, параллельной NP и проходящей через точку M.

не понятно, а также свои рекомендации по совершенствованию этой

презентации.