основания цилиндра на эту плоскость. Поэтому, если плоскость параллельна
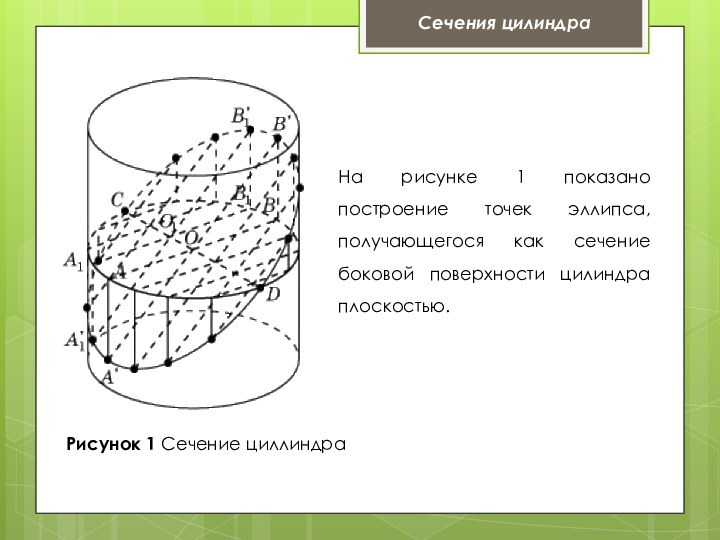
плоскости основания, то в сечении получается круг, равный основанию.Если плоскость сечения составляет некоторый угол с плоскостью основания цилиндра и не пересекает основания, то в сечении будет фигура, ограниченная эллипсом.
Сечения цилиндра