- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Системы двух линейных уравнений с двумя переменными
Содержание
- 2. Решить уравнение:
- 5. Метод подстановки: Итак, сможете назвать алгоритм решения системы двух уравнений с двумя переменными методом подстановки?
- 6. Решаем вместе!Решить уравнение методом подстановки. Делаем вместе,
- 7. Решить систему уравнений: 1)Чтобы решить эту
- 8. А теперь решим вот такое уравнение
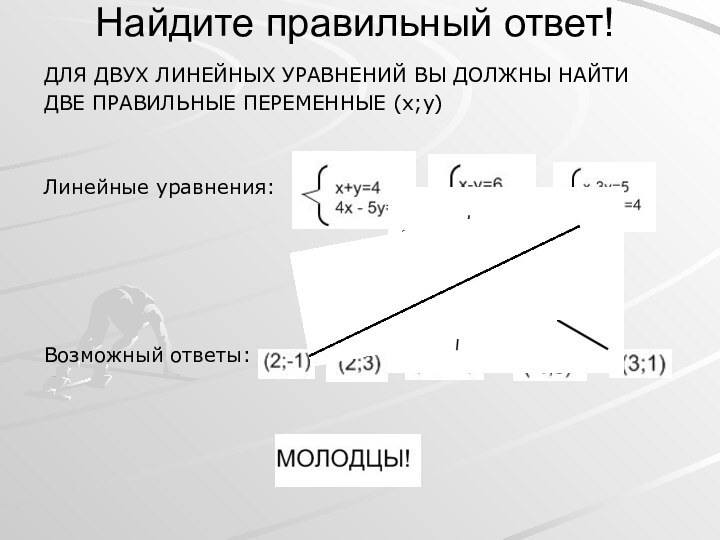
- 9. Найдите правильный ответ!ДЛЯ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ ВЫ ДОЛЖНЫ НАЙТИ ДВЕ ПРАВИЛЬНЫЕ ПЕРЕМЕННЫЕ (x;y) Линейные уравнения:Возможный ответы:
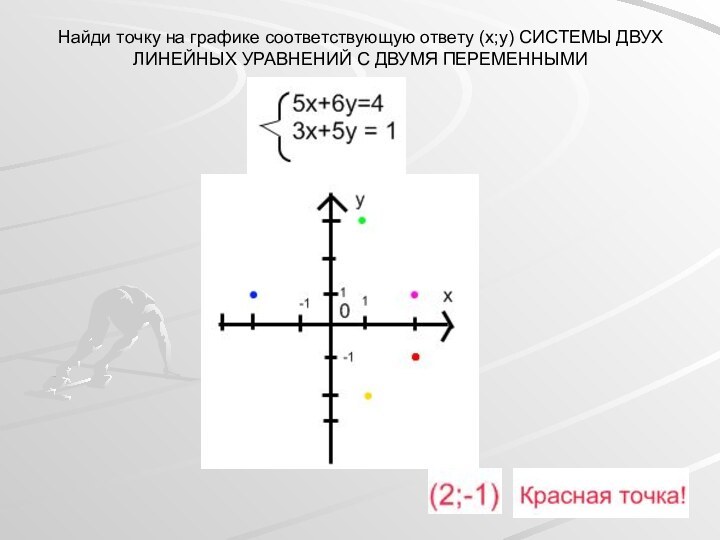
- 10. Найдите ответ!
- 11. Найдите ответ! Ответы все не подходят! Правильный???(-6;5)
- 12. Скачать презентацию
- 13. Похожие презентации
Решить уравнение:










Слайд 5
Метод подстановки:
Итак, сможете назвать алгоритм решения системы
двух уравнений с двумя переменными методом подстановки?
Слайд 6
Решаем вместе!
Решить уравнение методом подстановки. Делаем вместе, всё
по
порядку!
1) Выразим в первом уравнении y через
x: 2)Подставим полученное на первом шаге выражение вместо y во
второе уравнение системы:
3)Решить полученное на втором шаге уравнение относительно x:
4)Подставить найденное на третьем шаге значение x в выражение
y через x, полученное на первом шаге.
Слайд 7
Решить систему уравнений:
1)Чтобы решить эту систему,
нам
нужно убрать y (игреки).
Для этого y(игреки) должны быть равны
(допустим
2y и 2y или 7y и 7y).Вычтем второе уравнение из первого:
2) Подставим найденное значение x=2 в первое уравнение заданной
системы, т.е. в уравнение 2x+3y=1
3)Пара x=2, y=-1 – решение заданной системы
Ответ: (2;-1)
Слайд 8
А теперь решим вот такое уравнение методом
АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ!
1)Здесь сразу исключить переменную x или переменную y
из обоих уравнений с помощью сложения или вычитания уравнений не удастся.
Давайте умножим все члены второго уравнения на два! И посмотрим что
получится!
2) Да, да теперь с помощью вычитания можно убрать X.
Подставим y в первое или во второе уравнение и запишем ответ!
Ответ: (-0,25 ; 0)