- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему соответствия
Содержание
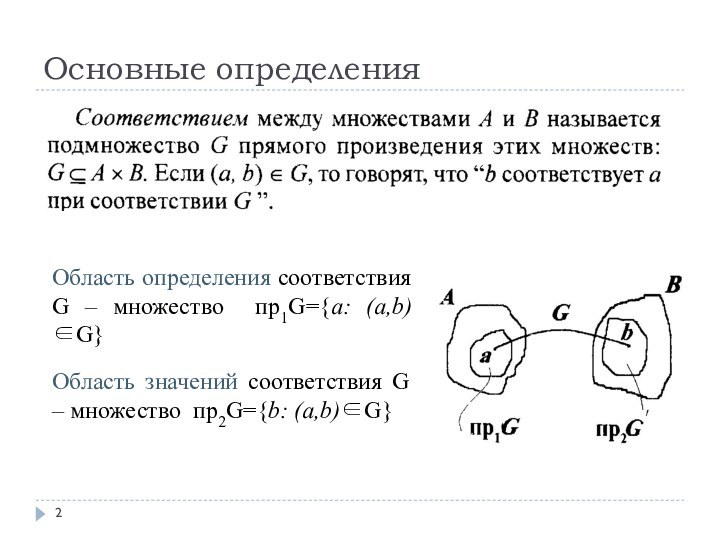
- 2. Основные определенияОбласть определения соответствия G – множество пр1G={a: (a,b)∈G}Область значений соответствия G – множество пр2G={b: (a,b)∈G}
- 3. Основные определенияПример 1. Экзаменационная ведомость устанавливает следующее
- 4. G={(Иванов, 4), (Петров, 2), (Сидоров, 3), (Конев,
- 5. Основные определенияВ примере 1:образом Иванова является 4;образом
- 6. Свойства соответствийСоответствие G⊆А×В называется всюду (полностью) определенным,
- 7. Свойства соответствийОпределим свойства отношения в примере 1.Частично
- 8. Свойства соответствийчастично определено, несюръективно, функционально, инъективноЧастично определено, сюръективно, нефункционально, инъективно
- 9. Свойства соответствийВсюду определено, несюръективно, функционально, инъективноВсюду определено, сюръективно, функционально, неинъективноВсюду определено, сюръективно, функционально, инъективно
- 10. Домашняя работа: определите свойства соответсвий.Придумайте пример соответствия, которое обладает свойствами: всюдоопределено, несюръективно, нефункционально, инъективно3Свойства соответствий
- 11. )
- 12. G⊆R+×R+Найти образы и прообразы чисел: 0, 1, 2; отрезков: [0,1], [2,3]
- 13. Пример 3. Соответствие G ⊆ R× R+
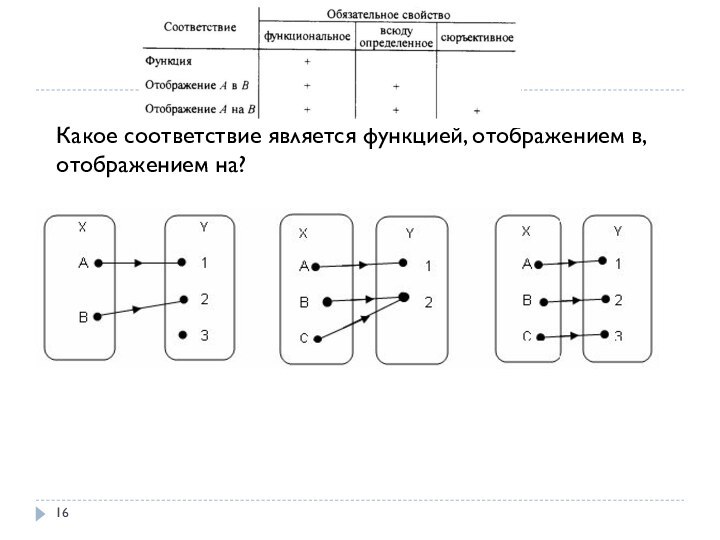
- 14. Функции и отображенияФункциональное соответствие называется функцией.Если функция
- 15. Функции и отображенияОтображением А в В называется
- 16. Какое соответствие является функцией, отображением в, отображением на?
- 17. Функции и отображения
- 18. Взаимно-однозначное соответствиеСоответствие называется взаимно-однозначным, если оно всюду определено, сюръективно, функционально и инъективно.
- 19. Какое соответствие является взаимно-однозначным?
- 20. Взаимно-однозначное соответствие
- 21. Мощность множествПонятие мощности возникает при сравнении множеств
- 22. Мощность множествЭтот факт позволяет:установить равенство мощностей двух
- 23. Счетные множестваЛюбое множество, равномощное множеству всех натуральных
- 24. Счетные множестваЕсли элемент множества М есть ν(n)
- 25. Счетные множестваПример. Множество всех нечетных натуральных чисел
- 26. Счетные множестваПример. Множество Z всех целых чисел
- 27. Счетные множестваПример. Множество Z всех целых чисел
- 28. Счетные множестваПримеры счетных множеств:Множество рациональных чисел счетно;Множество
- 29. Счетные множестваДокажем, что Множество пар натуральных чисел счетно.
- 30. Счетные множестваТеорема . (а) Подмножество счетного множества
- 31. Несчетные множестваТеорема Кантора: Множество всех действительных чисел
- 32. Примеры континуальных множеств:Множество действительных чисел; Множество иррациональных
- 33. Скачать презентацию
- 34. Похожие презентации







![соответствия G⊆R+×R+Найти образы и прообразы чисел: 0, 1, 2; отрезков: [0,1], [2,3]](/img/tmb/15/1431654/507a1bf458ae3a59154d42ee5141124c-720x.jpg)


















Слайд 3
Основные определения
Пример 1. Экзаменационная ведомость устанавливает следующее соответствие
:
А={Иванов, Петров, Сидоров, Конев, Синицын, Васечкин, Макарова}.
В={2, 3, 4,
5}.Иванов – 4
Петров – 2
Сидоров – 3
Конев – 4
Синицын на экзамен не явился
Васечкин – 3
Макарова – 5
G ⊆ А×В, G-соответствие между студентами и оценками
Слайд 4 G={(Иванов, 4), (Петров, 2), (Сидоров, 3), (Конев, 4),
(Васечкин, 3), (Макарова, 5)}.
Область определения соответствия G –
пр1G={Иванов,
Петров, Сидоров, Конев, Васечкин, Макарова}.Область значений соответствия G – пр2G={2, 3, 4, 5}.
Основные определения
А={Иванов, Петров, Сидоров, Конев, Синицын, Васечкин, Макарова}.
В={2, 3, 4, 5}.
Слайд 5
Основные определения
В примере 1:
образом Иванова является 4;
образом Сидорова
- 3 и т.д.
Прообразом 2 является Петров;
Прообразом 4 –
Иванов, Конев.
Слайд 6
Свойства соответствий
Соответствие G⊆А×В называется всюду (полностью) определенным, если
область определения совпадает с множеством А, т.е. пр1G=А. В
противном случае соответствие называется частично определенным.Соответствие G⊆А×В называется сюръективным, если область значений совпадает с множеством В, т.е. пр2G=В.
Соответствие G⊆А×В называется функциональным, если образом любого элемента а из области определения пр1G является единственный элемент b из области значений пр2G.
Соответствие G⊆А×В называется инъективным, если прообразом любого элемента b из области значений пр2G является единственный элемент а из области определения пр1G.
Слайд 7
Свойства соответствий
Определим свойства отношения в примере 1.
Частично определено,
так как нет образа для Синицына;
Сюръективно, так как для
каждой оценки определен прообраз;Функционально, так как каждому студенту соответствует единственная оценка;
Неинъективно, так как оценка 4 соответствует двум студентам.
G={(Иванов, 4), (Петров, 2), (Сидоров, 3), (Конев, 4), (Васечкин, 3), (Макарова, 5)}.
А={Иванов, Петров, Сидоров, Конев, Синицын, Васечкин, Макарова}.
В={2, 3, 4, 5}.
пр1G={Иванов, Петров, Сидоров, Конев, Васечкин, Макарова}.
пр2G={2, 3, 4, 5}.
Слайд 8
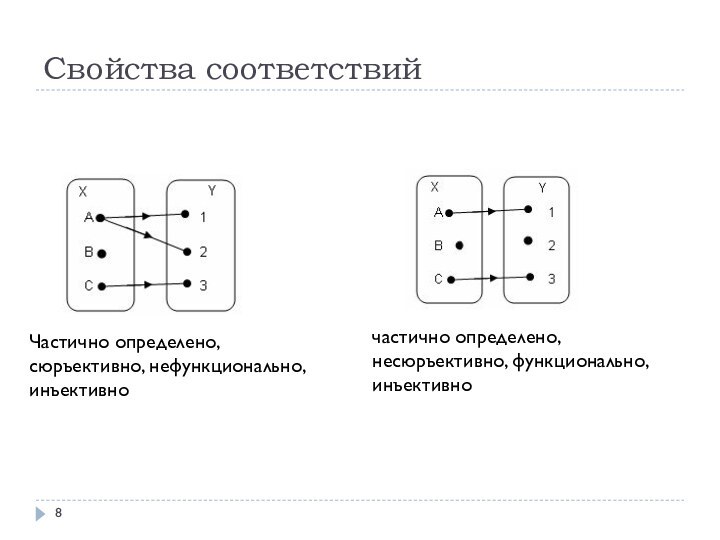
Свойства соответствий
частично определено, несюръективно, функционально, инъективно
Частично определено, сюръективно,
нефункционально, инъективно
Слайд 9
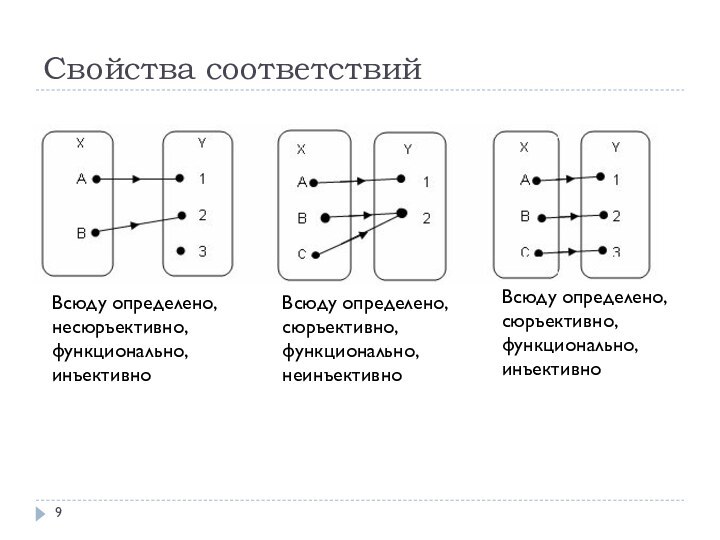
Свойства соответствий
Всюду определено, несюръективно, функционально, инъективно
Всюду определено, сюръективно,
функционально, неинъективно
Всюду определено, сюръективно, функционально, инъективно
Слайд 10
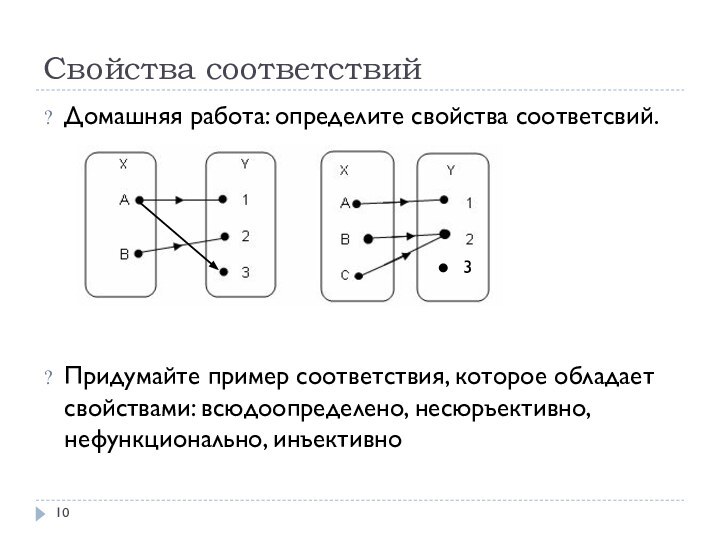
Домашняя работа: определите свойства соответсвий.
Придумайте пример соответствия, которое
обладает свойствами: всюдоопределено, несюръективно, нефункционально, инъективно
3
Свойства соответствий
Слайд 13 Пример 3. Соответствие G ⊆ R× R+ задано
графиком. Найти образы и прообразы чисел: 0, 2, 3;
отрезков [0,2], [-1,2]. Определить свойства соответствия.
Слайд 14
Функции и отображения
Функциональное соответствие называется функцией.
Если функция f
устанавливает соответствие между множествами А и В, то говорят,
что функция имеет тип А→В (обозначается f : А→В).Каждому элементу а из области определения функция f ставит в соответствие элемент b из области значений. Это обозначается f(а)=b. Элемент а называется аргументом функции, элемент b – значение функции на а.
Слайд 15
Функции и отображения
Отображением А в В называется всюду
определенная функция f : А→В (обозначается f : А
В).Отображением А на В называется всюду определенная и сюръективная функция f : А→В (обозначается f : А В).
Слайд 17
Функции и отображения
тип
Как нужно определить эту функцию, чтобы она стала отображением N на N
Слайд 18
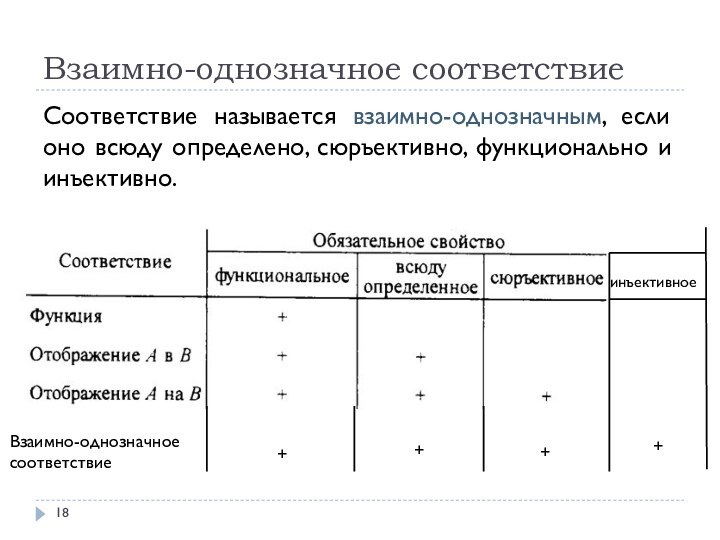
Взаимно-однозначное соответствие
Соответствие называется взаимно-однозначным, если оно всюду определено,
сюръективно, функционально и инъективно.
Слайд 21
Мощность множеств
Понятие мощности возникает при сравнении множеств по
числу элементов.
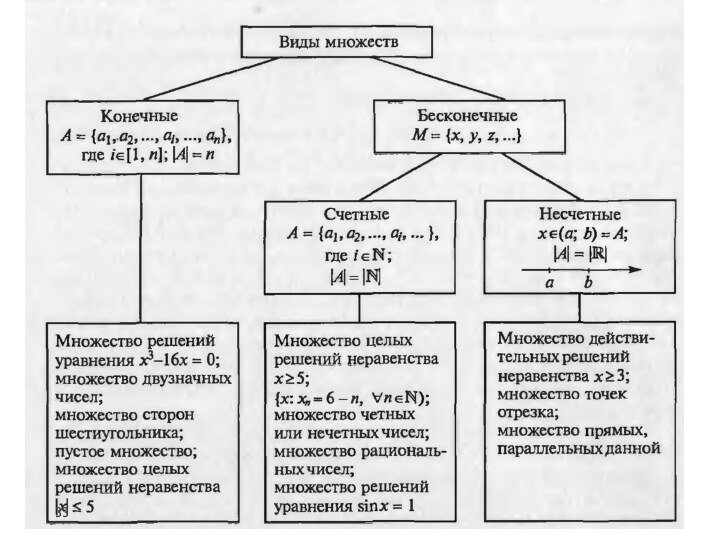
Мощностью конечного множества является число его элементов. Множество,
не являющееся конечным, называется бесконечным.Если между множествами А и В существует взаимно-однозначное соответствие, то мощности этих множеств равны, т.е. ⏐А⏐=⏐В⏐. В таком случае говорят, что множества А и В равномощны.
Слайд 22
Мощность множеств
Этот факт позволяет:
установить равенство мощностей двух множеств,
не вычисляя этих множеств;
вычислить мощность множества, установив его взаимно-однозначное
соответствие с множеством, мощность которого известна или легко вычисляема.Существование биекции между двумя эквивалентными множествами позволяет переносить изучение свойств с одного множества на другое, когда природа элементов не важна. Например, если |А|=n, то с элементами множества А можно работать как с числами 1,2,...,n.
Слайд 23
Счетные множества
Любое множество, равномощное множеству всех натуральных чисел,
называют счетным. Мощность счетного множества обозначают ℵ0 (читается „алеф
нуль").Если некоторое множество М равномощно множеству натуральных чисел N, то между М и N можно установить взаимно однозначное соответствие (биекцию) ν: N→ М, которое называют нумерацией счетного множества М.
Слайд 24
Счетные множества
Если элемент множества М есть ν(n) для
некоторого n∈ N, то этот элемент множества М обозначаем
через an, называя натуральное число n номером элемента аn относительно данной нумерации ν.Таким образом, элементы счетного множества можно перенумеровать, записав их в виде последовательности а1, ..., аn, ...
Слайд 25
Счетные множества
Пример. Множество всех нечетных натуральных чисел счетно.
Нумерацию ν можно задать так: ν(n) = 2n-1,
N={1, 2, 3, 4, 5, 6, 7, …}M2n-1- счетно.
M2n-1={1, 3, 5, 7, 9, 11, 13, …}
Получили:
M2n-1⊂ N;
⏐M2n-1⏐=⏐N⏐.
Множество равномощно своему подмножеству.
Слайд 26
Счетные множества
Пример. Множество Z всех целых чисел счетно.
Расположим элементы множества целых чисел в определенном порядке:
N={1, 2,
3, 4, 5, 6, 7, 8, 9, …}Z={0, -1, 1, -2, 2, -3, 3, -4, 4, … }
Получили:
N ⊂ Z;
⏐N⏐=⏐Z⏐
Нумерацию ν можно задать так:
- n/2, n- четное
ν(n) =
(n-1)/2, n - нечетное
Слайд 27
Счетные множества
Пример. Множество Z всех целых чисел счетно.
Нумерацию
можно было установить так:
Z={…, -5, -4, -3, -2,
-1, 0, 1, 2, 3, 4, … }Получили:
N ⊂ Z;
⏐N⏐=⏐Z⏐.
1
2
3
4
5
6
7
8
9
10
Слайд 28
Счетные множества
Примеры счетных множеств:
Множество рациональных чисел счетно;
Множество периодических
дробей счетно;
Множество всех натуральных чисел, делящихся на заданное число
к ≥ 2, счетно. Множество пар натуральных чисел счетно.
Слайд 30
Счетные множества
Теорема .
(а) Подмножество счетного множества конечно
или счетно.
(б) Всякое бесконечное множество содержит счетное подмножество.
(в) Объединение
конечного или счетного числа конечных или счетных множеств конечно или счетно.
Слайд 31
Несчетные множества
Теорема Кантора: Множество всех действительных чисел интервала
(0,1) числовой оси несчетно.
Всякое множество, эквивалентное множеству всех действительных
чисел интервала (0,1), называется континуальным или множеством мощности континуума.
Слайд 32
Примеры континуальных множеств:
Множество действительных чисел;
Множество иррациональных чисел
;
Множество точек на отрезке [0,5];
Множество точек квадрата [1,10]×[1,10];
Множество β(М)
всех подмножеств некоторого счетного множества ММножество точек пространства R3.





























