- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Способы нахождения наибольшего общего делителя и наименьшего общего кратного натуральных чисел
Содержание
- 2. Способы нахождения наибольшего общего делителя двух или нескольких натуральных чисел
- 3. 1. Способ, основанный на каноническом представлении натурального числа.2. Алгоритм Евклида.
- 4. Нахождение наибольшего общего делителя через каноническое разложении
- 5. Например:Найти D (448;656)Представим каждое число в каноническом виде.44822242112256228214277165623282164282241411
- 6. Замечание:Если натуральные числа a и b представлены
- 7. D(448;656)==16Выберем общие множители и найдем их произведение.
- 8. Наибольший общий делитель двух натуральных чисел a
- 9. Это утверждение основано на трех умозаключениях1.Если a
- 10. На основе этого утверждения Евклид сформулировал алгоритм вычисления наибольшего общего делителя двух натуральных чисел.
- 11. Алгоритм ЕвклидаПусть a>b1.Если a делится на b,
- 12. Алгоритм ЕвклидаD(a,b)a>ba=bg+rданетD=bконецD=rконецданетданетконец
- 13. Например:Найти D (448;656)Разделим 656 на 448 с остатком. Значит, D(448;656)= 166564481448-2084482416-322086192-1632232-0656=448∙1+ 208448=208∙2+ 32208=32∙6+1632=16∙2+0
- 14. Задача: Найти НОД (120,540, 418) НОД(a,b,c)=НОД(D(a,b),c)Значит: 1.
- 15. Способы нахождения наименьшего общего кратного двух или нескольких натуральных чисел
- 16. 1. Способ, основанный на каноническом представлении натурального
- 17. Нахождение наименьшего общего кратного через каноническое разложение
- 18. Например:Найти К(448;656)Представим каждое число в каноническом виде.44822242112256228214277165623282164282241411
- 19. Замечание:Если натуральные числа a и b представлены
- 20. K(448;656)=Выберем все множители и найдем их произведение.
- 21. 2) Способ образования НОК натуральных чиселa·b=D(a,b)·K(a,b)K(a,b)=
- 22. Например:Найти К(448;656)K(a,b)=
- 23. Задача: найдите НОК (12,48,54).Решение:Так как 48 кратно 12, то НОК (12,48,54)==НОК (48,54); НОД(48,54)=6 НОК(48,54)=
- 24. Скачать презентацию
- 25. Похожие презентации
Способы нахождения наибольшего общего делителя двух или нескольких натуральных чисел
Слайд 4
Нахождение наибольшего общего делителя через каноническое разложении чисел
1.
Представить каждое число в каноническом виде.
2. Выбрать общие простые
множители.3. Составить произведение общих простых множителей.
4. Значение этого произведения равно наибольшему общему делителю.
Слайд 5
Например:
Найти D (448;656)
Представим каждое число в каноническом виде.
448
2
224
2
112
2
56
2
28
2
14
2
7
7
1
656
2
328
2
164
2
82
2
41
41
1
Слайд 6
Замечание:
Если натуральные числа a и b представлены в
каноническом виде, то каждый множитель в состав НОД (a,b)
входит с наименьшим показателем.
Слайд 8
Наибольший общий делитель двух натуральных чисел a и
b равен последнему, не равному нулю, остатку от деления
числа a на b (если a>b) или b на a (если b>a).
2) Древнегреческим математикам
был известен факт:
Слайд 9
Это утверждение основано на трех умозаключениях
1.Если a делится
на b, то D(a,b)=b.
2.Если a=bg+r, где a,b,r отличны
от 0, то множество делителей a и b совпадает с множеством общих делителей b и r.3. Если a=bg+r, где a,b,r отличны от 0, то D(a,b)=D(b,r).
Слайд 10
На основе этого утверждения Евклид сформулировал алгоритм вычисления
наибольшего общего делителя двух натуральных чисел.
Слайд 11
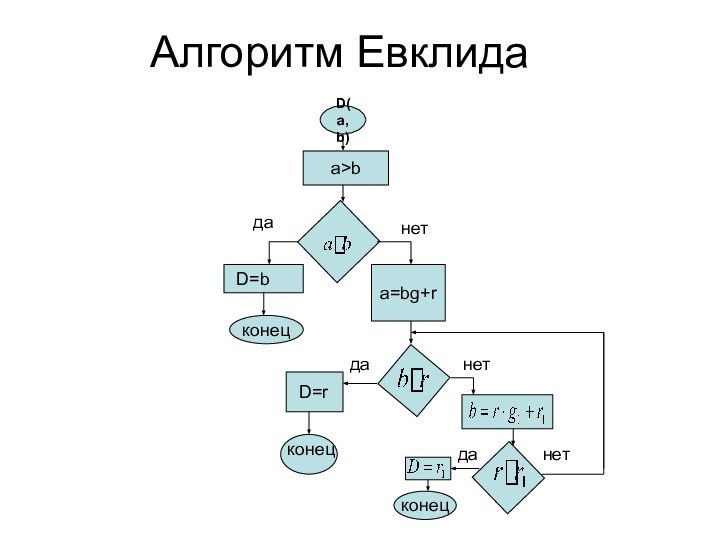
Алгоритм Евклида
Пусть a>b
1.Если a делится на b, то
D(a;b)=b.
Если при делении a на b, получается остаток r,
то D(a;b)=D(b;r)=r, если b кратно r.Если при делении b на r получается остаток
то, D(a,b)=D(b,r)=D
Слайд 13
Например:
Найти D (448;656)
Разделим 656 на 448 с остатком.
Значит, D(448;656)= 16
656
448
1
448
-
208
448
2
416
-
32
208
6
192
-
16
32
2
32
-
0
656=448∙1+ 208
448=208∙2+ 32
208=32∙6+16
32=16∙2+0
Слайд 14
Задача: Найти НОД (120,540, 418)
НОД(a,b,c)=НОД(D(a,b),c)
Значит: 1. Найдем
НОД(120,540)
НОД (120,540)=60.
2.
Найдем НОД(60,418)НОД(60,418)=2.
Слайд 16
1. Способ, основанный на каноническом представлении натурального числа.
2.
Способ, основанный на взаимосвязи между НОД(a,b) и НОК(a,b)
Слайд 17
Нахождение наименьшего общего кратного через каноническое разложение чисел
1.
Представить каждое число в каноническом виде.
2. Выбрать все простые
множители.3. Составить произведение всех простых множителей.
4. Значение этого произведения равно наименьшему общему кратному.
Слайд 18
Например:
Найти К(448;656)
Представим каждое число в каноническом виде.
448
2
224
2
112
2
56
2
28
2
14
2
7
7
1
656
2
328
2
164
2
82
2
41
41
1
Слайд 19
Замечание:
Если натуральные числа a и b представлены в
каноническом виде, то каждый множитель в состав НОК (a,b)
входит с наибольшим показателем.
Слайд 23
Задача: найдите НОК (12,48,54).
Решение:
Так как 48 кратно 12,
