- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему
Содержание
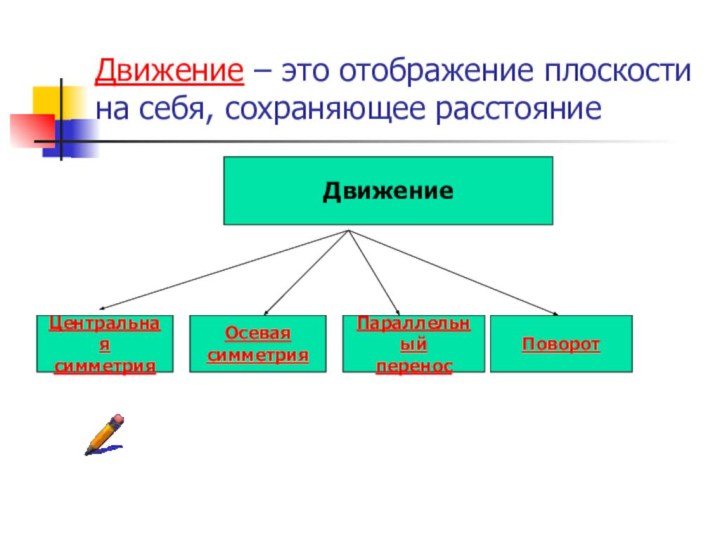
- 2. Движение – это отображение плоскости на себя, сохраняющее расстояниеДвижениеЦентральнаясимметрияОсевая симметрияПараллельныйпереносПоворот
- 3. Центральная симметрия. Определение. Две точки А
- 4. Определение. Фигура называется симметричной относительно точки О,
- 5. Осевая симметрияОпределение. Две точки А и А1
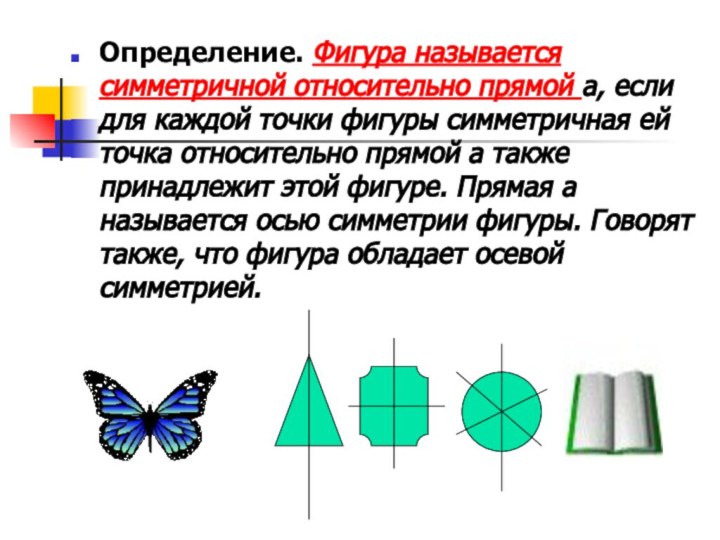
- 6. Определение. Фигура называется симметричной относительно прямой а,
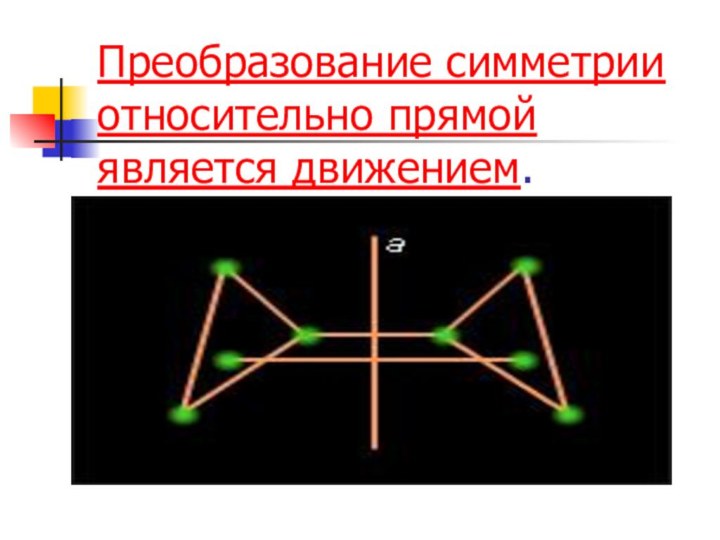
- 7. Преобразование симметрии относительно прямой является движением.
- 8. Поворот относительно центра O есть отображение плоскости
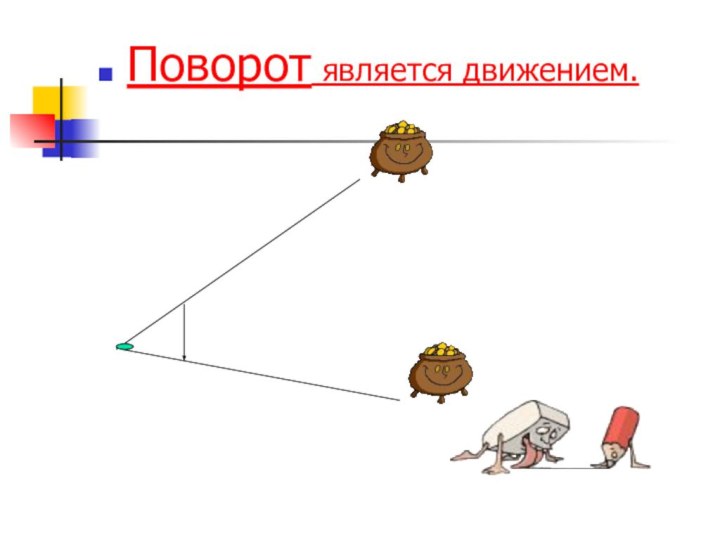
- 9. Поворот является движением.
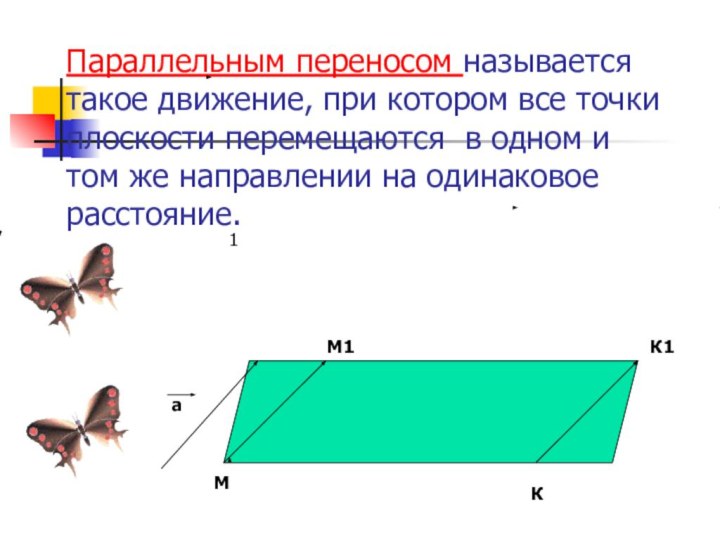
- 10. Параллельным переносом называется такое движение, при котором
- 11. Параллельный перенос Параллельный перенос является движением, т.е.
- 12. Скачать презентацию
- 13. Похожие презентации







Слайд 3
Центральная симметрия
. Определение.
Две точки А и
А1 называются симметричными относительно точки О, если О -
середина отрезка АА1. Точка О считается симметричной самой себеОпределение.
А
А1
О
Слайд 4
Определение.
Фигура называется симметричной относительно точки О, если
для каждой точки фигуры симметричная ей точка относительно точки
О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.Центральная симметрия
Определение.
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.
Центральная симметрия
Определение.
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.
Центральная симметрия
Определение.
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.
О
Слайд 5
Осевая симметрия
Определение. Две точки А и А1 называются
симметричными относительно прямой а, если эта прямая проходит через
середину отрезка АА1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.А
А1
Слайд 6
Определение. Фигура называется симметричной относительно прямой а, если
для каждой точки фигуры симметричная ей точка относительно прямой
а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.
Слайд 8 Поворот относительно центра O есть отображение плоскости не
себя, при котором каждой точке X плоскости ставится в соответствие такая
точка X', что, во-первых, OX'=OX, во-вторых угол XOX` равен заданному и, в-третьих, луч OX' откладывается от луча OX в заданном направлении. Причем, если угол положительный, то движение осуществляется против часовой стрелки, а если отрицательный, то по часовой. Точка O называется центром поворота, а угол XOX`- углом поворота.Слайд 10 Параллельным переносом называется такое движение, при котором все
точки плоскости перемещаются в одном и том же направлении
на одинаковое расстояние.1
М
М1
К
К1
а