на множестве X Є D(f), если для любых двух
элементов x1 и х2 множества Х, таких, что x1 < x2 , выполняется неравенствоf(x1) < f(x2).
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть













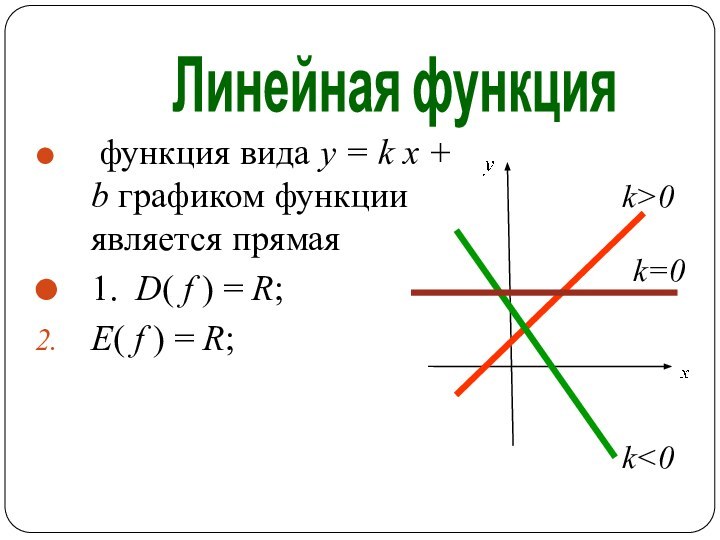



k>0
k<0
k=0
k
x
k>0
k<0
Функция корня
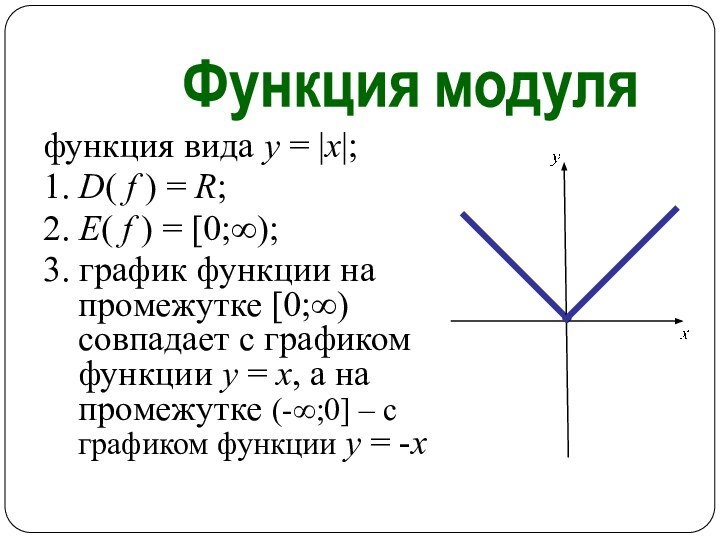
Функция модуля