- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Зеркальная симметрия
Содержание
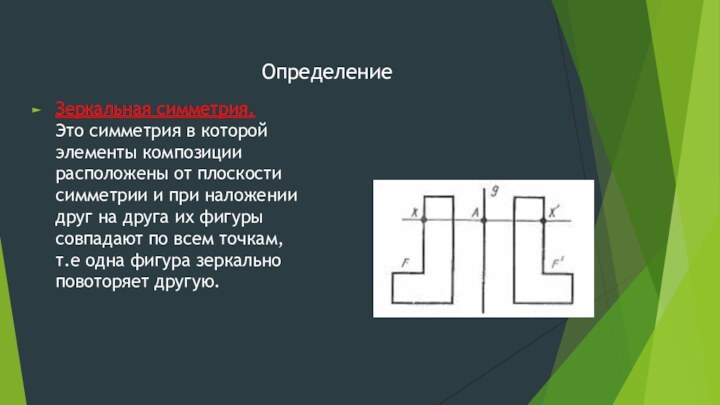
- 2. Определение Зеркальная симметрия. Это симметрия в которой
- 3. Виды симметрии: а) Лучевая симметрия б) Осевая симметрия в) Центральная симметрия г) Зеркальная симметрия
- 4. Фигуры, симметричные относительно плоскостиФигуры, симметричные относительно плоскости.
- 5. Это математическое понятие описывает соотношение в оптике
- 6. Геометрическая фигура называется симметричной относительно плоскости S , если для каждой
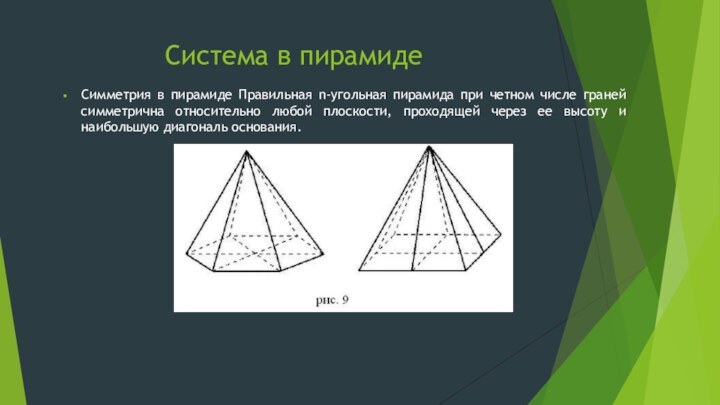
- 7. Система в пирамиде Симметрия в пирамиде Правильная
- 8. Симметрия правильной пирамидыОсь симметри: при четном числе
- 9. Термин зеркальная симметрия употребляется также для описания
- 10. Скачать презентацию
- 11. Похожие презентации
Определение Зеркальная симметрия. Это симметрия в которой элементы композиции расположены от плоскости симметрии и при наложении друг на друга их фигуры совпадают по всем точкам, т.е одна фигура зеркально повоторяет другую.