Слайд 2
Оборудование:
компьютер
экран
проектор
модели окружности
Тесьма
Чертёжные инструменты
Вид урока: интегрированный (т.к. в нём
есть элементы различных видов уроков: беседа, лекция, практическая самостоятельная
работа, анализ ситуации, устный опрос, письменная работа, контролирующая работа-тест).
Технология: развивающего обучения, индивидуализации.
Слайд 3
Цели и задачи урока:
Образовательные:
познакомить учащихся с формулой длины
окружности;
отрабатывать навыки округления десятичных дробей;
познакомить с историей возникновения математических
понятий;
приобретение навыков исследовательской работы;
закреплять умения и навыки использования формул для вычисления длины окружности.
Развивающие:
развивать математическую речь, память, умение анализировать, обобщать и делать выводы;
развивать познавательный интерес к предмету, логическое мышление, пространственное воображение.
Воспитательные:
воспитывать прилежание, аккуратность, трудолюбие, чувство коллективизма, умение слушать и слышать.
Слайд 4
Отгадайте загадку, и вы узнаете, о чем пойдет
речь сегодня на уроке.
Если видишь солнце в небе, или
чашку с молоком
Видишь бублик или обруч, слышишь сказку с колобком,
В круглом зеркале увидел ты сейчас свою наружность.
И вдруг понял, что фигура называется …
(окружность).
Слайд 5
3,1415926
Округлите число
до целых
4- м; 3,141- т;
3,15- к;
3,2- е; 3,1415- р;
Д
Л
и
н
а
до десятых
до
сотых
до тысячных
до десятитысячных
3-д;
3,1-л;
3,14 -и;
3,142 - н;
3,1416 - а;
окружности
Слайд 6
Правильно, сегодня на уроке мы будем изучать длину
окружности.
Приведите примеры предметов окружающего мира, дающих представление об окружности
Слайд 7
План урока
Повторение основных понятий и определений;
Выполнение практической работы
(нахождение
значения числа практическим
путём);
Решение задач;
Мини-тест по пройденному материалу;
Подведение итогов;
Творческое домашнее задание.
Слайд 8
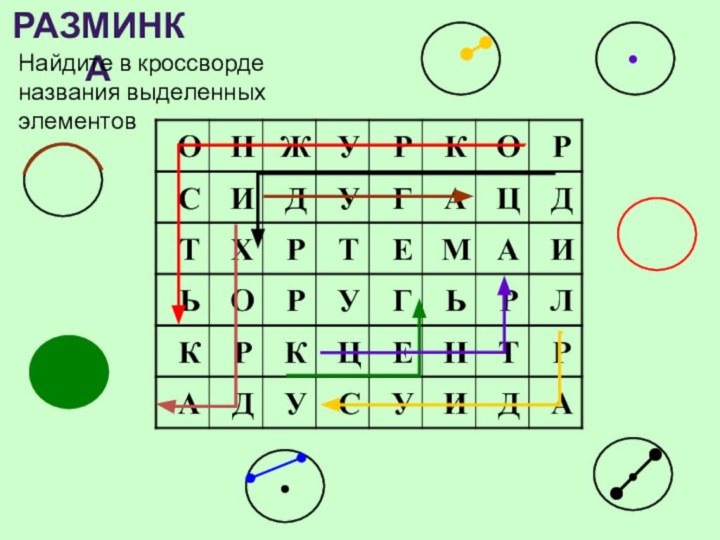
Разминка
Найдите в кроссворде названия выделенных элементов
Слайд 9
Окружность – геометрическая фигура, состоящая из точек плоскости,
равноудаленных от данной точки.
о
Слайд 10
Радиус окружности-
это отрезок, соединяющий центр
окружности с любой точкой
окружности.
А
О
r
Слайд 11
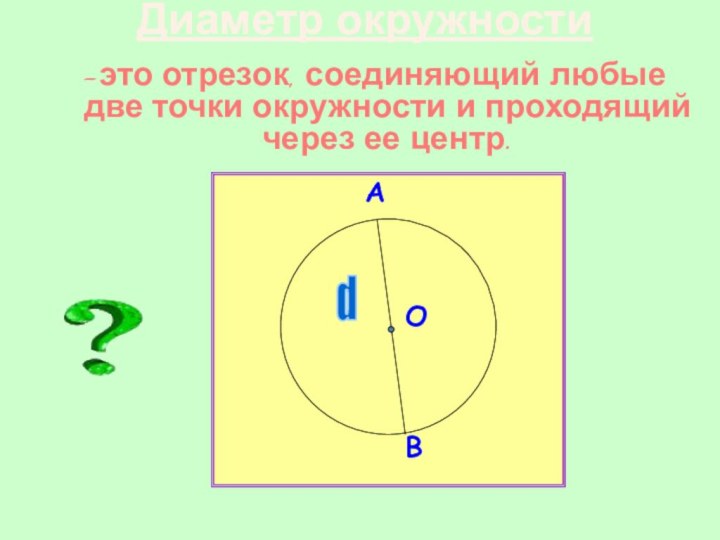
Диаметр окружности
-это отрезок, соединяющий любые две точки окружности
и проходящий через ее центр.
О
А
В
d
Слайд 12
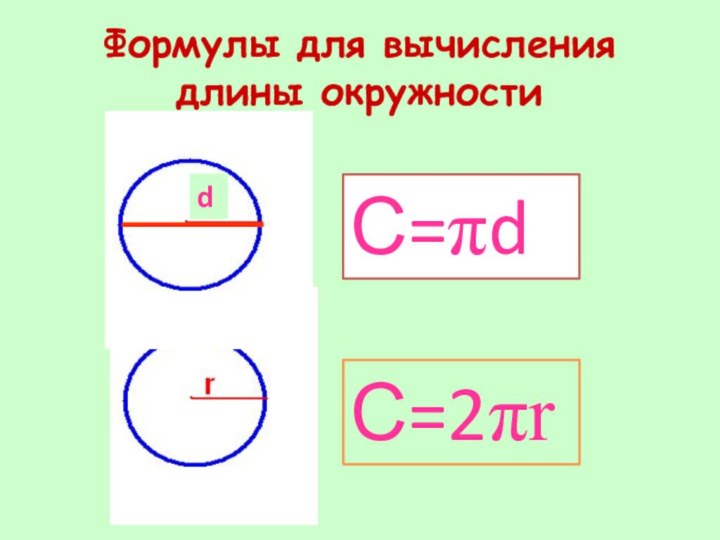
Формулы для вычисления длины окружности
С=πd
С=2πr
d
Слайд 13
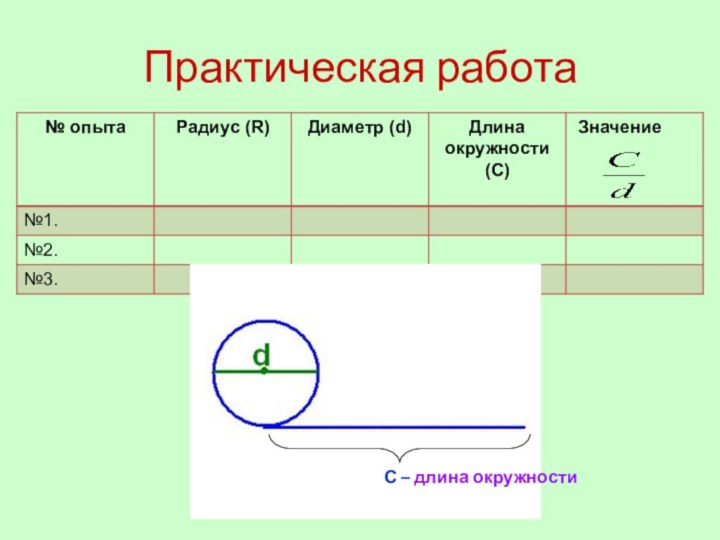
Практическая работа
С – длина окружности
Слайд 15
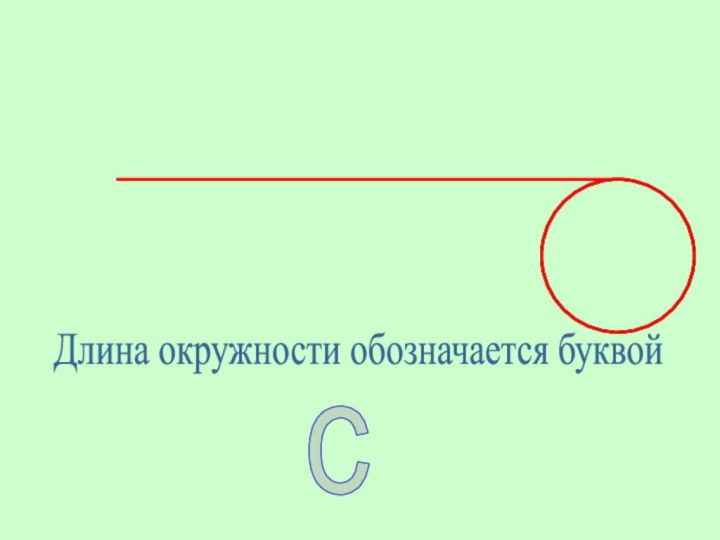
обведите окружность нитью, измерьте её длину и запишите;
Слайд 16
Длина окружности обозначается буквой
с
Слайд 17
с помощью линейки и циркуля измерьте диаметр
окружности и запишите его значение в тетрадь;
Слайд 18
вычислите отношение длины окружности к ее диаметру с
точностью до тысячных и округлите полученное число до сотых;
сравните
результат с числом 3,14
Слайд 19
План выполнения
практической работы
Получите карточку с тремя значениями радиуса
окружности (R);
Внесите данные в таблицу;
Постройте окружности данных радиусов;
Постройте диаметры
окружностей и измерьте их;
Внесите данные в таблицу;
Вычислите диаметры окружностей по формуле и убедитесь в правильности измерений;
С помощью нити измерьте длины окружностей;
Внесите данные в таблицу;
Вычислите отношение длины окружности к ее диаметру с точностью до тысячных и округлите полученное число до сотых;
Сравните результат с числом 3,14
Слайд 20
π≈3,14
22
число π – это бесконечная десятичная дробь.
Памятник числу
«пи» на ступенях перед зданием Музея искусств в Сиэтле
14
марта отмечается День пи – неформальный праздник математиков.
«Отцом» праздника стал Лари Шоу, обративший внимание на то, что этот день приходится на 3,14 в американской системе записи дат.
В Сиэтле установлена металлическая скульптура числа π.
Слайд 21
≈3,1415926535…
Обозначение числа происходит от первой буквы
греческого слова
периферия, что означает "окружность".
Слайд 22
Леонард Эйлер
Впервые обозначением этого числа греческой буквой
воспользовался британский математик Джонс в 1706 году, а общепринятым
оно стало после работ Леонарда Эйлера в 1737 году.
Слайд 23
=
22
7
π≈3,14
Архимед
«Архимедово число» . Более того,
он сумел оценить точность этого приближения:
Слайд 25
У Белого Кролика были часы со стрелками длиной
3 см и 5 см. Найди длины окружностей, которые
описывают своими концами стрелки, совершая полный круг.
3 см
5 см
Закрепление пройденного
Слайд 26
?
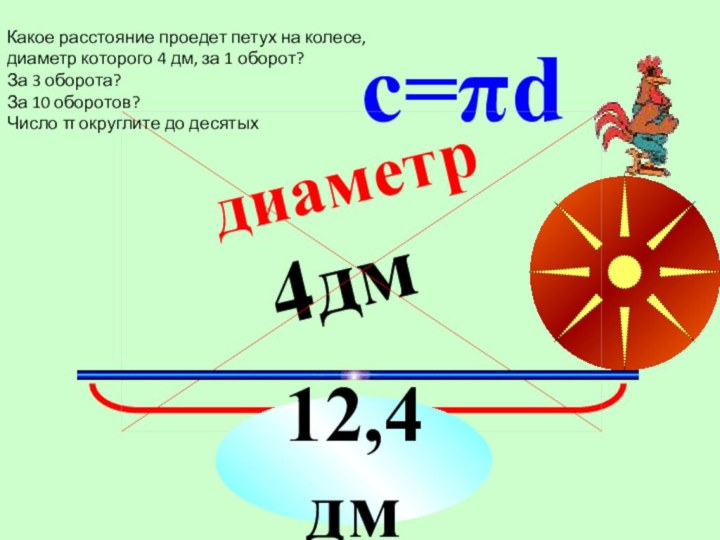
диаметр
4дм
c=πd
12,4дм
Какое расстояние проедет петух на колесе, диаметр
которого 4 дм, за 1 оборот?
За 3 оборота?
За 10 оборотов?
Число π округлите до десятых
Слайд 27
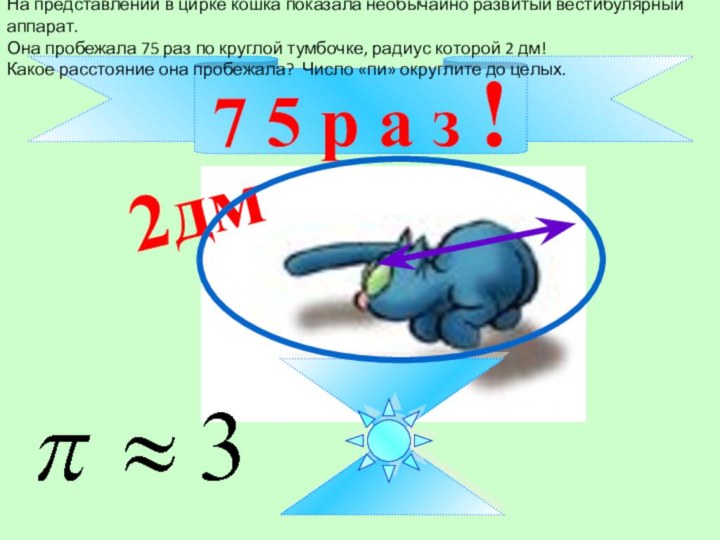
7 5 р а з !
2дм
На представлении в
цирке кошка показала необычайно развитый вестибулярный аппарат.
Она пробежала
75 раз по круглой тумбочке, радиус которой 2 дм!
Какое расстояние она пробежала? Число «пи» округлите до целых.
Слайд 28
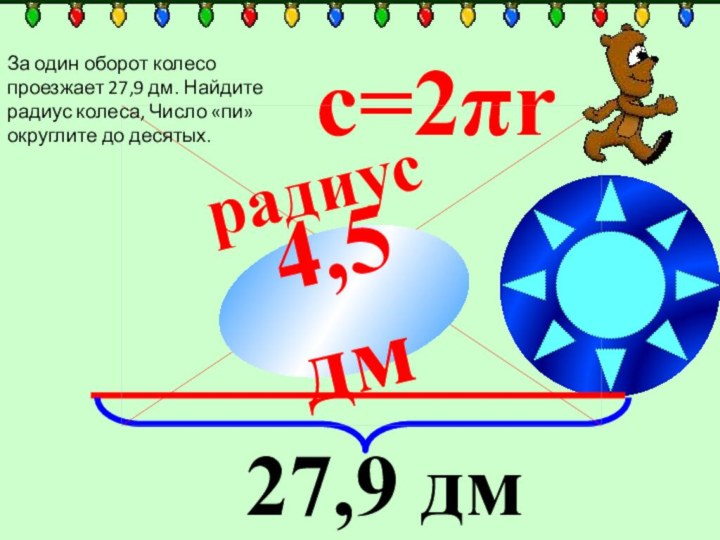
радиус
?
с=2πr
27,9 дм
4,5дм
За один оборот колесо
проезжает 27,9 дм. Найдите радиус колеса, Число «пи» округлите
до десятых.
Слайд 29
20м
300м/мин
2мин
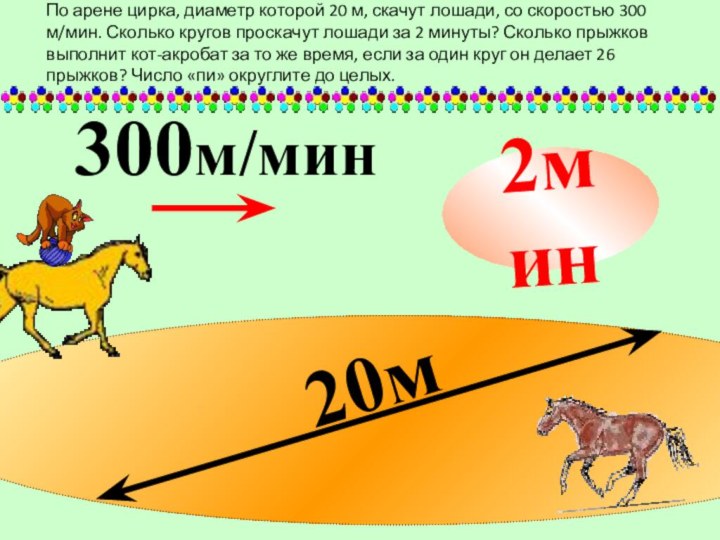
По арене цирка, диаметр которой 20 м, скачут
лошади, со скоростью 300 м/мин. Сколько кругов проскачут лошади
за 2 минуты? Сколько прыжков выполнит кот-акробат за то же время, если за один круг он делает 26 прыжков? Число «пи» округлите до целых.
1. Отрезок, соединяющий две точки окружности и проходящий через центр.
А) радиус; Б) сторона; В) хорда; Г) диаметр.
2. Число π равно
А) 3,14; Б) 1,34; В) 3,91; Г) 4,13.
3. Формула длины окружности
А) С=πr Б) С=πd В) C=2πd Г) C=2r
4. Чему равен диаметр окружности, радиус которой 3,8 см?
А) 6,28 Б) 1,57 В) 7,6 Г) 3,14
1.Отрезок, соединяющий две точки окружности и проходящий через центр.
А) радиус; Б) сторона; В) хорда; Г) диаметр.
2. Число π равно
А) 3,14; Б) 1,34; В) 3,91; Г) 4,13.
3. Формула длины окружности
А) С=πr Б) С=πd В) C=2πd Г) C=2r
4. Чему равен диаметр окружности, радиус которой 3,8 см?
А) 6,28 Б) 1,57 В) 7,6 Г) 3,14
Слайд 34
Сегодня на уроке мы:
1. Повторили…
2. Узнали…
3. Закрепили…
Слайд 35
Домашнее задание.
Придумать запоминающиеся рифмованные строки, позволяющие без труда
запомнить некоторое количество знаков после запятой в числе «
пи»;
Составить задачу по теме: « Длина окружности» и нарисовать к ней рисунок.
Слайд 36
Это я знаю и помню прекрасно:
Пи многие знаки
мне лишни, напрасны.
Доверимся знаньям громадным
Тех, пи кто сосчитал, цифр
армаду.
Двенадцать цифр можно запомнить с помощью следующих строк (количество букв в каждом слове соответствует цифре числа π)
«Это я знаю и помню прекрасно, «пи» многие знаки тут лишни, напрасны».
3,14-15-9-2-6-5-3-5-8
Или короче, задайте вопрос: Что я знаю о кругах? (3,1416).