- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Задачи на концентрацию, смеси и сплавы. Подготовка к ГИА
Содержание
- 2. Задачи на смеси и сплавы вызывают трудности,
- 3. Задачи на смеси и сплавы вызывают трудности,
- 4. Способов решения таких задач много. Эти способы разнообразны.
- 5. Старинный способ решения задач на концентрацию по
- 6. Старинный способ решения задач на концентрацию по
- 7. РЕШЕНИЕ: (от большего , естественно, отнимаем меньшее)
- 11. 40х + 48y = 42(х +
- 12. 3 способ0,4х + 0,48y = 0,42(х +
- 15. Сколько воды надо добавить в 1 л
- 16. Процент содержания меди в первом сплаве на
- 17. Процент содержания меди в первом сплаве на
- 18. II. Правило «креста»18
- 19. В сосуд, содержащий 5 л 12%-го водного раствора
- 20. Смешали некоторое количество 15%-го раствора некоторого вещества
- 21. Смешали 4 л 15%-го водного раствора некоторого вещества
- 22. Имеется два сплава. Первый сплав содержит 10%
- 23. Первый сплав содержит 10% меди, второй — 40%
- 24. Смешав 30%-й и 60%-й растворы кислоты и
- 25. Решение задачи12
- 26. Имеется два сосуда. Первый содержит 30 кг, а
- 27. Раствор30 кгх% = 0,01ху% = 0,01у68% =
- 28. Раствор100 кгх% = 0,01ху% = 0,01у70% =
- 29. Виноград содержит 90% влаги, изюм — 5%. Сколько
- 30. Даны два куска с различным содержанием олова.
- 31. Торговец продает орехи двух сортов. Первый по
- 32. САМОСТОЯТЕЛЬНО5. Торговец продает вино двух сортов:
- 33. САМОСТОЯТЕЛЬНО5. Торговец продает вино двух сортов:
- 34. Смешав 30% и 60% растворы кислоты и
- 35. 8. Смешав 70%-й и 60% -й
- 36. 10. Смешали 4л 15% водного раствора некоторого
- 37. 12. Имеются два сплава. Первый содержит 10%
- 38. Скачать презентацию
- 39. Похожие презентации
































Слайд 3
Задачи на смеси и сплавы вызывают трудности, связанные
с не пониманием химических процессов. Необходимо иметь ввиду, что
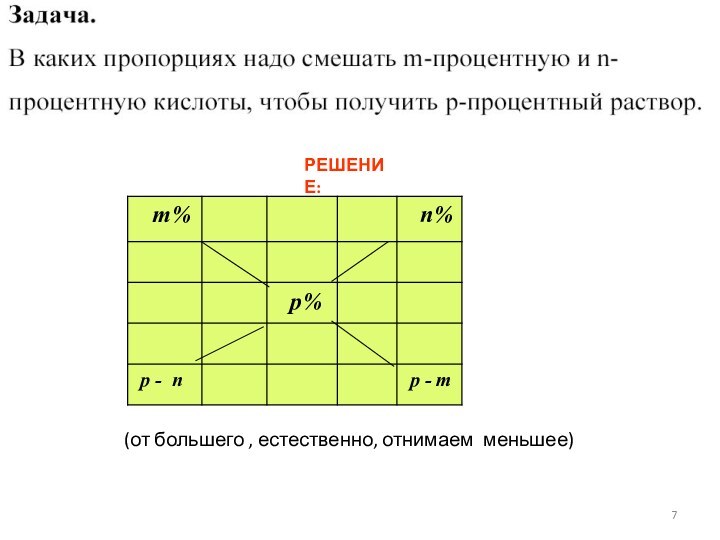
в задачах такого рода, предлагаемых на ГИА по математике, никаких химических процессов, влияющих на количественные соотношения задачи, не происходит.Слайд 5 Старинный способ решения задач на концентрацию по правилу
«креста»
В верхней строке записываются процентные содержания основного вещества в
имеющихся растворахПосредине записываем процентное содержание растворов в полученной смеси
В нижней строчке записываем разности процентных содержаний (вычитаем из большего числа меньшее и записываем на ту диагональ, где находятся соответственно уменьшаемое и вычитаемое )
Слайд 6 Старинный способ решения задач на концентрацию по правилу
«креста»
В верхней строке записываются процентные содержания основного вещества в
имеющихся растворахПосредине записываем процентное содержание растворов в полученной смеси
В нижней строчке записываем разности процентных содержаний (вычитаем из большего числа меньшее и записываем на ту диагональ, где находятся соответственно уменьшаемое и вычитаемое )
Слайд 8
задача1
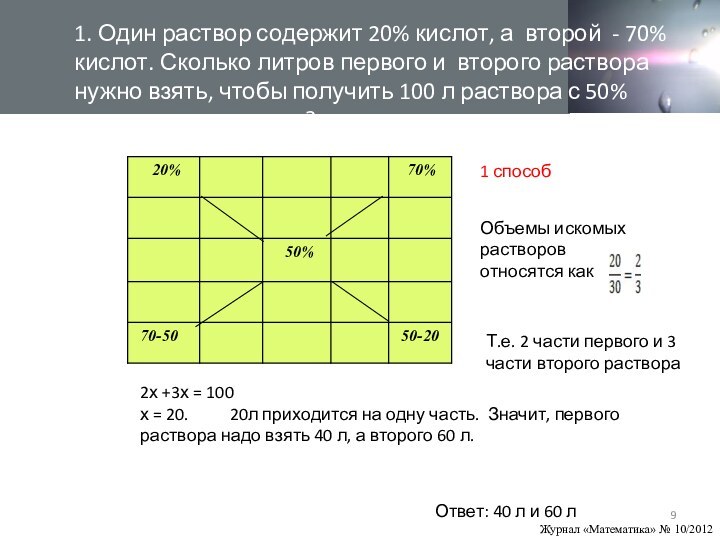
Объемы искомых растворов
относятся как Т.е. 2 части первого и 3 части второго раствора
2х +3х = 100
х = 20. 20л приходится на одну часть. Значит, первого раствора надо взять 40 л, а второго 60 л.
Ответ: 40 л и 60 л
1. Один раствор содержит 20% кислот, а второй - 70% кислот. Сколько литров первого и второго раствора нужно взять, чтобы получить 100 л раствора с 50% содержанием кислот?
1 способ
Слайд 9
задача1
Объемы искомых растворов
относятся как Т.е. 2 части первого и 3 части второго раствора
2х +3х = 100
х = 20. 20л приходится на одну часть. Значит, первого раствора надо взять 40 л, а второго 60 л.
Ответ: 40 л и 60 л
1. Один раствор содержит 20% кислот, а второй - 70% кислот. Сколько литров первого и второго раствора нужно взять, чтобы получить 100 л раствора с 50% содержанием кислот?
1 способ
Слайд 10
задача1
Значит,
первого раствора надо взять 40 л, а второго 60 л.Ответ: 40 л и 60 л
Один раствор содержит 20% кислот, а второй - 70% кислот. Сколько литров первого и второго раствора нужно взять, чтобы получить 100 л раствора с 50% содержанием кислот?
2 способ
+
=
х л
100-х л
100 л
20%
70%
50%
20х + 70 (100-х) = 50*100
20х + 7000 – 70х = 5000 -50х = -2000
х = 40
20%
Слайд 11
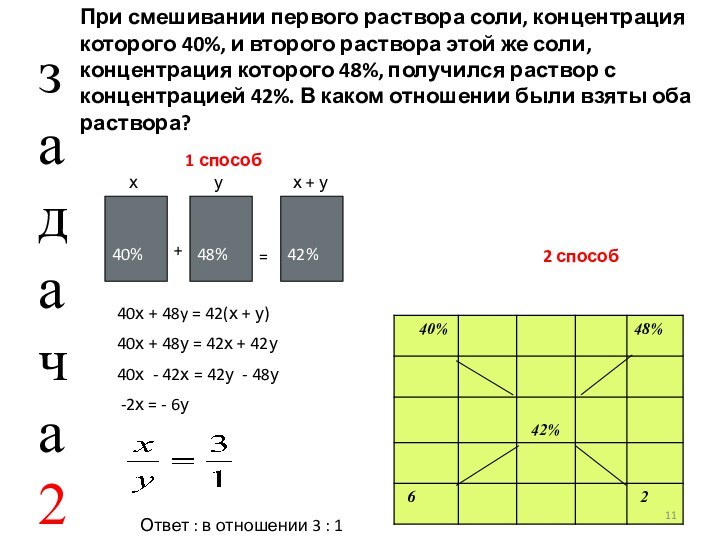
40х + 48y = 42(х + у)
40х
+ 48у = 42х + 42у
40х - 42х =
42у - 48у2х = - 6у
Ответ : в отношении 3 : 1
При смешивании первого раствора соли, концентрация которого 40%, и второго раствора этой же соли, концентрация которого 48%, получился раствор с концентрацией 42%. В каком отношении были взяты оба раствора?
40%
48%
42%
х
у
х + у
2 способ
1 способ
задача2
+
=
Слайд 12
3 способ
0,4х + 0,48y = 0,42(х + у)
0,4х
+ 0,48у = 0,42х + 0,42у
0,4х - 0,42х =
0,42у - 0,48у0,02х = - 0,06у
Ответ : в отношении 3 : 1
При смешивании первого раствора соли, концентрация которого 40%, и второго раствора этой же соли, концентрация которого 48%, получился раствор с концентрацией 42%. В каком отношении были взяты оба раствора?
задача2
Слайд 13
задача3
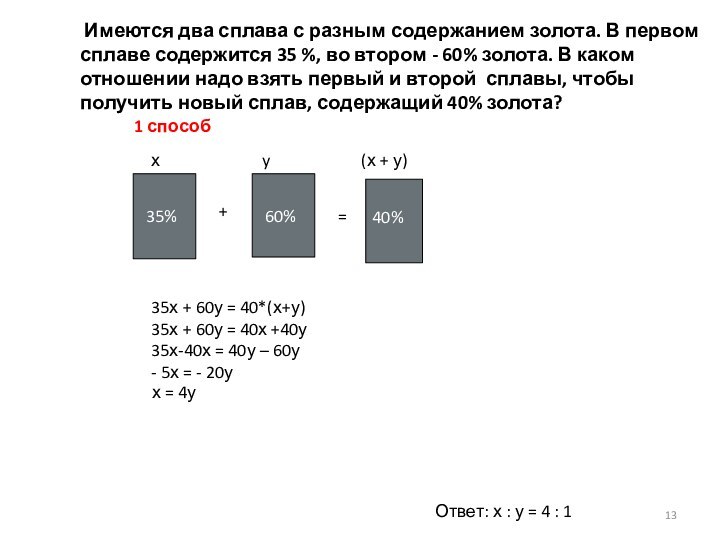
х = 4уОтвет: х : у = 4 : 1
Имеются два сплава с разным содержанием золота. В первом сплаве содержится 35 %, во втором - 60% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить новый сплав, содержащий 40% золота?
1 способ
+
=
х
y
(х + у)
35%
60%
40%
35х + 60у = 40*(х+у)
35х + 60у = 40х +40у 35х-40х = 40у – 60у
- 5х = - 20у
Слайд 14
задача3
х = 4уОтвет: х : у = 4 : 1
Имеются два сплава с разным содержанием золота. В первом сплаве содержится 35 %, во втором - 60% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить новый сплав, содержащий 40% золота.
2 способ
0,35х + 0,6у = 0,4(х+у)
0,35х + 0,6у = 0,4х +0,4у 0,35х-0,4х = 0,4у – 0,6у
-0,05х = - 0,2у
Пусть х – масса 1 сплава, а у – масса 2 сплава. Количество золота в 1 сплаве 0,35х, а 0,6у – во втором сплаве. Масса нового сплава (х +у), а количество золота в нем 0,4(х +у)
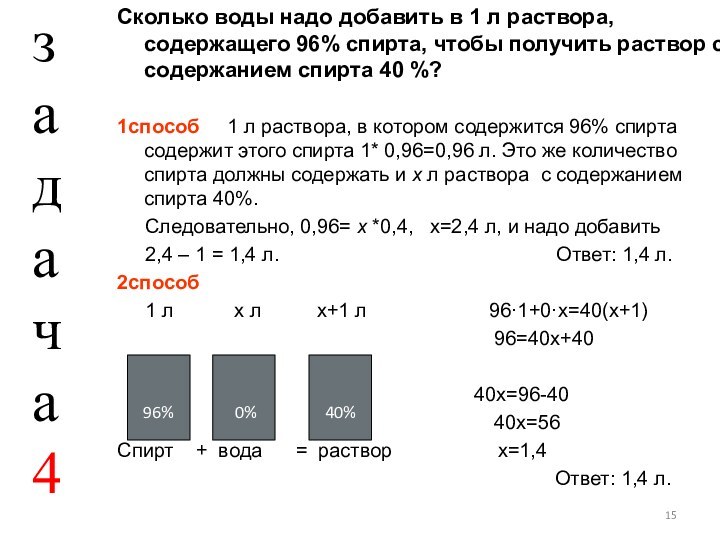
Слайд 15 Сколько воды надо добавить в 1 л раствора,
содержащего 96% спирта, чтобы получить раствор с содержанием спирта
40 %?1способ 1 л раствора, в котором содержится 96% спирта содержит этого спирта 1* 0,96=0,96 л. Это же количество спирта должны содержать и х л раствора с содержанием спирта 40%.
Следовательно, 0,96= х *0,4, х=2,4 л, и надо добавить
2,4 – 1 = 1,4 л. Ответ: 1,4 л.
2способ
1 л х л х+1 л 96·1+0·х=40(х+1)
96=40х+40
40х=96-40
40х=56
Спирт + вода = раствор х=1,4
Ответ: 1,4 л.
задача4
96%
0%
40%
Слайд 16 Процент содержания меди в первом сплаве на 40%
меньше, чем во втором сплаве. После того, как эти
слитки сплавили вместе, получили новый сплав с содержанием меди 36%.Определить процентное содержание меди в первоначальных сплавах, если в первом сплаве меди было 6 кг, а во втором 12 кг.1способ
Пусть х % меди содержалось в первом сплаве, тогда х + 40 % её содержалось во втором. В первом сплаве меди было 6 кг, а во втором 12кг,следовательно,1% первого и второго сплавов имели массы 6:х и 12 :(х + 40)кг соответственно. Поскольку каждый сплав составляет 100%, то их массы будут М1=6:х кг и М2=12:(х+40) соответственно.
Новый сплав содержит меди то же количество, которое было до сплавления в двух слитках, т.е. 6+12=18 кг. Это по условию задачи составляет 36% нового сплава, поэтому масса нового сплава есть: 18:36*100=50 кг.
Масса нового сплава состоит из масс двух старых сплавов, так что 50= (6:х)+ 12:(х+40)
1= (12:х)+ 24:(х+40).
х1=20, х2=-24; х>0,то х=20. 20%+40%=60%
Ответ: 20%, 60%
задача5
Слайд 17 Процент содержания меди в первом сплаве на 40%
меньше, чем во втором сплаве. После того, как эти
слитки сплавили вместе, получили новый сплав с содержанием меди 36%.Определить процентное содержание меди в первоначальных сплавах, если в первом сплаве меди было 6 кг, а во втором 12 кг.2способ
задача5
Х%
Х +40%
36%
+
=
M1=6:х
M2=12:(х+40)
6:х + 12:(х+40)
Меди 6 кг
Меди 12 кг
Меди 18 кг
18:36=0,5 M нового сплава
6:х + 12:(х+40) = 0,5
+
= 1
12(х+40)+24х= х(х+40)
12х+480+24х= х2 + 40х
х2 + 4х + 480 = 0
х1=20,
х2=-24 –посторонний корень
Значит, 20% меди в 1 сплаве, 20%+40%=60% - во втором
Слайд 18
II. Правило «креста»
18
15
15 0 3
Значит, 40 кг – 15 частей, тогда, чтобы получить 15% р-р, нужно добавить 3 части воды
40:15·3=8 кг.
Ответ: 8 кг
Задача 6.Сироп содержит 18% сахара. Сколько кг воды нужно добавить к 40 кг сиропа, чтобы содержание сахара составило 15% ?
I. Пусть надо добавить х кг воды. Заполним таблицу по условию задачи.
Составим и решим уравнение:
0,15(40+х)=0,18· 40
х=8
Ответ: 8 кг.
Слайд 19 В сосуд, содержащий 5 л 12%-го водного раствора некоторого
вещества, добавили 7 л воды. Сколько процентов составляет концентрация получившегося
раствора? (Ответ: 5%)Задача 7 (прототип 99571) 7
Раствор
5 л
7 л
12 л
12% = 0,12
0%
х% = 0,01х
Вещество
0,12 · 5
0 · 7
0,01х · 12
+
=
Слайд 20 Смешали некоторое количество 15%-го раствора некоторого вещества с
таким же количеством 19%-го раствора этого вещества. Сколько процентов
составляет концентрация получившегося раствора?Задача 8 (прототип №99572) 2
Раствор
100 г
100 г
200 г
15% = 0,15
19% = 0,19
х% = 0,01х
Вещество
0,15 · 100 г
0,19 · 100 г
0,01х · 200 г
+
=
Слайд 21 Смешали 4 л 15%-го водного раствора некоторого вещества с
6 л 25%-го водного раствора этого же вещества. Сколько процентов
составляет концентрация получившегося раствора? Задача 3Раствор
4 л
6 л
10 л
15% = 0,15
25% = 0,25
х% = 0,01х
Вещество
0,15 · 4 л
0,25 · 6 л
0,01х · 10 л
+
=
. Задача 9 (прототип №99573)
Слайд 22
Имеется два сплава. Первый сплав содержит 10% никеля,
второй — 30% никеля. Из этих двух сплавов получили третий
сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?Задача 10
Сплав
х кг
(200 – х) кг
200 кг
10% = 0,1
30% = 0,3
25% = 0,25
Никель
0,1х кг
0,3(200 – х) кг
0,25 · 200 кг
+
=
Слайд 23
Первый сплав содержит 10% меди, второй — 40% меди.
Масса второго сплава больше массы первого на 3 кг.
Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.Задача11
Сплав
х кг
(х + 3) кг
(2х + 3) кг
10% = 0,1
40% = 0,4
30% = 0,3
Никель
0,1х кг
0,4(х + 3) кг
+
=
0,3(2х + 3) кг
Слайд 24 Смешав 30%-й и 60%-й растворы кислоты и добавив
10 кг чистой воды, получили 36%-й раствор кислоты. Если
бы вместо 10 кг воды добавили 10 кг 50%-го раствора той же кислоты, то получили бы 41%-й раствор кислоты. Сколько килограммов 30%-го раствора использовали для получения смеси?Задача 12
Слайд 26 Имеется два сосуда. Первый содержит 30 кг, а второй —
20 кг раствора кислоты различной концентрации. Если эти растворы
смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?Задача 13
Слайд 27
Раствор
30 кг
х% = 0,01х
у% = 0,01у
68% = 0,7
Кислота
0,01х
· 30 кг
0,68 · 50 кг
+
=
К задаче 13
1 случай
0,01у
· 20 кг20 кг
50 кг
Слайд 28
Раствор
100 кг
х% = 0,01х
у% = 0,01у
70% = 0,7
Кислота
0,01х
· 100 кг
0,7 · 200 кг
+
=
К задаче 13
2 случай
0,01у
· 100 кг100 кг
200 кг
Слайд 29 Виноград содержит 90% влаги, изюм — 5%. Сколько кг
винограда требуется для получения 20 кг изюма?
Задача 14
Решение.
Так
как в изюме воды 5%, то сухого вещества 95% от общей массы изюма.20 · 0,95 = 19 кг сухого вещества.
Так как в винограде воды 90%, то сухого вещества 10% от общей массы.
Значит, в винограде 19 кг сухого вещества, что составляет 10%.
19 : 0,1 = 190 кг — требуется взять винограда.
Слайд 30 Даны два куска с различным содержанием олова. Первый,
массой 300 г. содержит 20% олова. Второй, массой 200
г, содержит 40% олова. Сколько % олова будет содержать сплав, полученный из этих кусков? (28%)В сосуд, содержащий 5 л 12% водного раствора кислоты, добавили 7л воды. Сколько % составляет концентрация, получившегося раствора? (5%)
САМОСТОЯТЕЛЬНО
Слайд 31 Торговец продает орехи двух сортов. Первый по 90
центов, второй по 60 центов за 1 кг. Он
хочет получить 50 кг смеси по 72 цента за кг. Сколько потребуется взять орехов каждого сорта? (20 кг, 30 кг)Сколько фунтов меди надо сплавить с 75 фунтами серебра 72-й пробы, чтобы получить серебро 64-й пробы? (9,375 фунта)
САМОСТОЯТЕЛЬНО
Слайд 32
САМОСТОЯТЕЛЬНО
5. Торговец продает вино двух сортов: по
10 и по 6 гривен за ведро. Какие
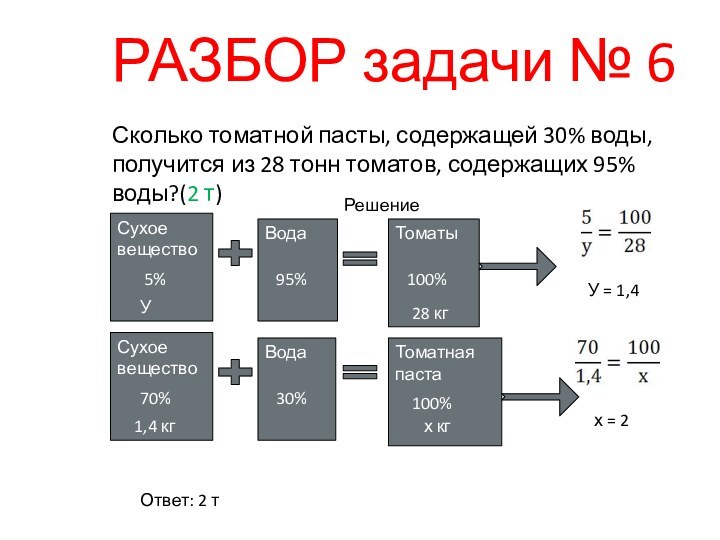
части этих вин ему надо взять, чтобы получить вино ценой в 7 гривен за ведро? (1/4 ведра и ¾ ведра)6. Сколько томатной пасты, содержащей 30% воды, получится из 28 тонн томатов, содержащих 95% воды?(2 т)
Слайд 33
САМОСТОЯТЕЛЬНО
5. Торговец продает вино двух сортов: по
10 и по 6 гривен за ведро. Какие
части этих вин ему надо взять, чтобы получить вино ценой в 7 гривен за ведро? (1/4 ведра и ¾ ведра)6. Сколько томатной пасты, содержащей 30% воды, получится из 28 тонн томатов, содержащих 95% воды?(2 т)
Слайд 34 Смешав 30% и 60% растворы кислоты и добавив
10кг чистой воды, получили 36% раствор кислоты. Если бы
вместо 10 кг воды добавили 10 кг 50% раствора этой же кислоты, то получили бы 41% раствор кислоты. Сколько килограммов 30% раствора использовали для получения смеси? (60 кг)При смешивании первого раствора кислоты 20% концентрации со вторым - 50% концентрации, получили 30% раствор кислоты. В каком отношении были взяты первый и второй растворы?(2 : 1)
САМОСТОЯТЕЛЬНО
Слайд 35 8. Смешав 70%-й и 60% -й растворы
кислоты и добавив 2 кг чистой воды, получили 50%
раствор кислоты. Если бы вместо 2кг воды добавили 2 кг 90% раствора той же кислоты, то получили бы 70% раствор кислоты. Сколько кг 70% раствора использовали для получения смеси? (3 кг)9. Первый сплав содержит 5% меди, второй - 13% меди. Масса второго сплава больше массы первого на 2 кг. Сплавив их вместе, получили третий сплав, содержащий 10% меди. Найти массу третьего сплава. (8 кг)
САМОСТОЯТЕЛЬНО
Слайд 36 10. Смешали 4л 15% водного раствора некоторого
вещества с 6 л 25% водного раствора этого же
вещества. Сколько % составляет концентрация получившегося раствора? (21%)11. Смешали некоторое количество 15% раствора некоторого вещества с таким же количеством 19% раствора этого же вещества. Сколько % составляет концентрация получившегося раствора? (17%)
САМОСТОЯТЕЛЬНО
Слайд 37 12. Имеются два сплава. Первый содержит 10% никеля,
второй – 30% никеля, из этих двух сплавов получили
третий сплав, массой 200 кг, содержащий25% никеля. На сколько килограммов масса первого сплава меньше массы второго сплава? (на 100 кг)13. Первый сплав содержит 10 % меди, второй сплав – 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найти массу третьего сплава. (9кг)
САМОСТОЯТЕЛЬНО