Слайд 2
Актуальность темы
1. Показать значимость задач практического характера в
понимании курса алгебры и начала анализа.
2. Обратить внимание
авторов учебников математики и учителей математики на объединение математики со всем спектром наук, изучаемых в рамках общеобразовательной школы(усилить задания, иллюстрирующие прикладные аспекты математики в астрономии, физике, географии, биологии, в гуманитарных науках).
3. Определять роль математических знаний в своей будущей профессии.
Слайд 3
Показать значимость математических моделей для применения в практической
деятельности, для изучения смежных дисциплин, для продолжения образования.
Цель:
Слайд 4
Гипотеза
Изучение математических моделей реальных процессов в природе и
обществе поможет преодолеть затруднение в применении математических знаний, полученных
на уроках.
Слайд 5
“Этот мировой порядок не создан никем из богов
и никем из людей, но он был, есть и
будет вечно живым огнем, мерами угасающим и мерами вспыхивающим”.
Если попытаться нарисовать себе общую картину периодических явлений и процессов в мире так и хочется сказать словами Гераклита:
Слайд 6
Математика – это язык плюс рассуждения, концентрированный результат
точного мышления
многих людей.
Слайд 7
Математика и
Физика
Физик не может не знать
математический
язык потому,
что на этом языке написана книга природы,
которую суждено ему читать. Физик не может рассуждать иначе, как только математически, потому, что он претендует на точность.
Слайд 8
“Автомобиль массой 2100 кг движется с ускорением 0,5
м/с2. Найти силу тяги двигателя, если коэффициент трения равен
0,02.
Кл.рук
Слайд 9
Математика и
Химия
Уже более двухсот лет прошло с
тех пор, как химия перестала быть описательной наукой. После
того, как гениальный М.В. Ломоносов, ввел в химическую практику весы, знание математики стало необходимо для каждого химика. Еще в 1741 году М.В. Ломоносов писал: “Если математики из сопоставления нескольких линий выводят очень многие истины, то и для химиков я не вижу никакой иной причины, вследствие которой они не могли бы вывести больше закономерностей из такого обилия имеющихся опытов, кроме незнания математики”.
Слайд 10
Решение. Т.к. медь переходит в раствор с каждой
грани равномерно, то в определённый момент реакции в кислоте
будет присутствовать куб, но уже меньших размеров
Пусть х – ребро куба, тогда объём куба равен .
Так как ,
то изменение объёма куба куб.см.
Считая приближённо - изменение длины ребра куба
и учитывая, что имеем:
Следовательно, (см).
Ответ: 0,0016 см
Задача При изучении свойств концентрированной серной кислоты учитель поместил медный кубик с ребром 5 см в раствор кислоты. Через некоторое время масса кубика уменьшилась на 0,96 г. Требуется определить, на сколько уменьшились размеры куба, то есть, на сколько укоротилось его ребро, если плотность меди равна 8 г/см3. (Медь переходила в раствор с каждой грани равномерно).
Слайд 11
Математика и География
Из дисциплины преимущественно собирающей и
классифицирующей факты, она постепенно превращается в науку о пространственных
взаимосвязях явлений на земле, познающую закономерности этих взаимосвязей.
Происходит процесс создания новой теоретической или математической географии, цель которой – установление пространственных закономерностей, связывающих отдельные области географии в единую систему наук.
Слайд 12
Смена в некоторой экологической системе подчиняется принципам периодичности
и цикличности (луг – болото, болото – луг). Нам
известен закон, по которому она происходит: h(t)= -
Требуется найти размах между циклами смены (т.е. найти разницу между положениями "болото" и "луг" на графике функции h(t)).
Для того чтобы найти наибольшее и наименьшее значения данной функции, необходимо отыскать её область значений.
В силу того, что -1≤cos4t≤1, то
Сл. h(t) [6;8], где 8 – наибольшее значение функции ("луг"), а 6 –наименьшее ("болото").
Тогда размах равен 8 – 6 = 2.
Ответ: 2.
, где t – время.
Решение. Пусть наибольшему значению функции h(t) соответствует положение "луг", а наименьшему – "болото". Преобразуем функцию
Слайд 13
Математика и
Астрономия
Математика, физика и астрономия – родные
сестры, весьма почтенного возраста, но не стареющие, а молодеющие,
живущие в дружбе и союзе. Плодом этого союза явились наши «Востоки», «Восходы», «Союзы», бороздящие безбрежное пространство, получившее с легкой руки Пифагора название «космос».
Слайд 14
Астрономы и географы
издавна пользовались
сферическими координатами.
Планета Планета
Солнце
Планета
Земля
Полярная звезда
Планета
Слайд 15
Вес космонавта на Земле 90 кг. Перед стартом
корабля он полулежит в кресле, площадь опоры которого 0,5
кв.м. Как космонавт будет давить на кресло во время подъема корабля, если перегрузка равна 8 g?
Слайд 16
Биологи давно прибегают к математике.
Ценность математики
для биологии состоит в применении ее как аппарата исследований,
и в возможности абстрактно подойти к решению сложнейших проблем и обнаружить связи между принципиально различными явлениями и процессами.
Математика и Биология
Слайд 17
В среду с определёнными условиями существования вносят популяцию
из 100 бактерий. Численность популяции возрастает по закону:
где t
выражено в часах. Найти максимальный размер этой популяции до момента её угасания.
Найдём производную от функции z(t):
но – 1 не удовлетворяет условию задачи, значит необходимо рассмотреть поведение производной функции в окрестности точки 1.
Видно, что 1 – точка максимума.
А это и говорит о том, что в момент времени t = 1 (час) популяция достигнет своего наибольшего значения (будет иметь максимальный размер).
Тогда =150 бактерий.
Ответ:150 бактерий.
Слайд 18
История
и обществоведение
«Любая гуманитарная наука лишь тогда чего-нибудь
стоит, если она доказана математическим способом»
Р.Кеттелл
Историю нельзя
представить без дат, без сопоставлений экономики, достижений науки и техники, развития общества
Слайд 19
1914 г.
Одним из показателей глубокого кризиса экономики являлось
закрытие промышленных предприятий, главным образом слабо связанных с выпуском
военной продукции.
Слайд 20
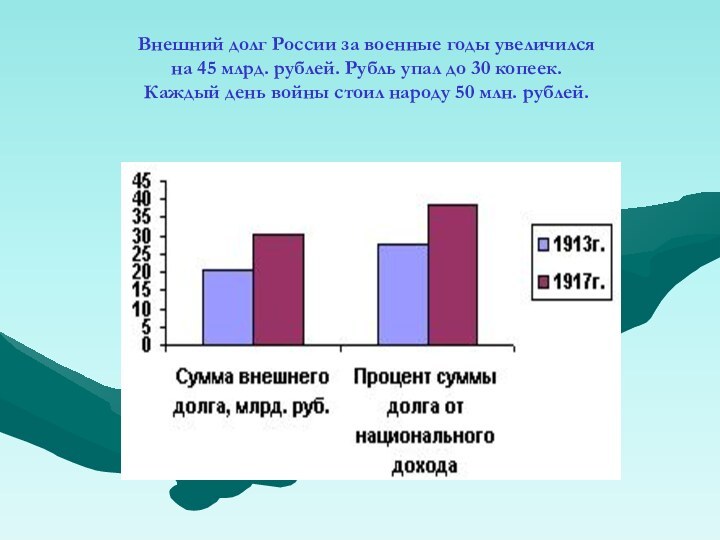
Внешний долг России за военные годы увеличился
на
45 млрд. рублей. Рубль упал до 30 копеек.
Каждый
день войны стоил народу 50 млн. рублей.
Слайд 21
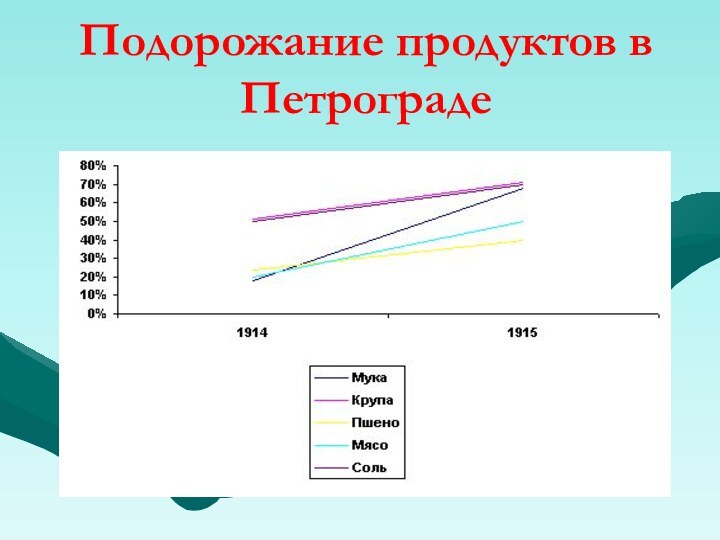
Подорожание продуктов в Петрограде
Слайд 22
Русский язык
и литература
Многие слышали о машинном переводе,
о стихах, сочиненных машинами, о расшифровке математиками языка, исчезнувшего
народа майя, о достижениях новой науки – математического языкознания. Мы хотим рассказать о другом – о фактах счастливого соединения художественного и математического талантов наблюдаемого у некоторых людей.
Слайд 23
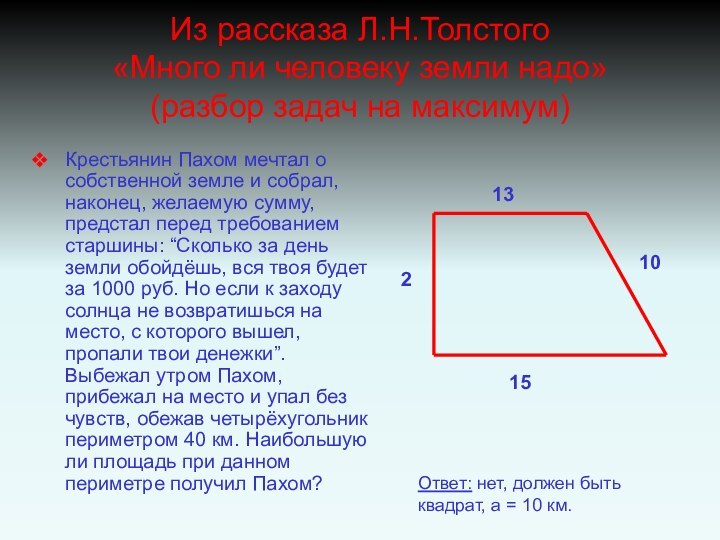
Из рассказа Л.Н.Толстого
«Много ли человеку земли надо»
(разбор
задач на максимум)
Крестьянин Пахом мечтал о собственной земле и
собрал, наконец, желаемую сумму, предстал перед требованием старшины: “Сколько за день земли обойдёшь, вся твоя будет за 1000 руб. Но если к заходу солнца не возвратишься на место, с которого вышел, пропали твои денежки”. Выбежал утром Пахом, прибежал на место и упал без чувств, обежав четырёхугольник периметром 40 км. Наибольшую ли площадь при данном периметре получил Пахом?
Ответ: нет, должен быть квадрат, а = 10 км.
Слайд 24
Сегодня в условиях массового производства, изучением проблем качества
и красоты предметов труда занимаются разные науки: техническая эстетика,
стандартизация и квалиметрия
Трудовое обучение
Слайд 25
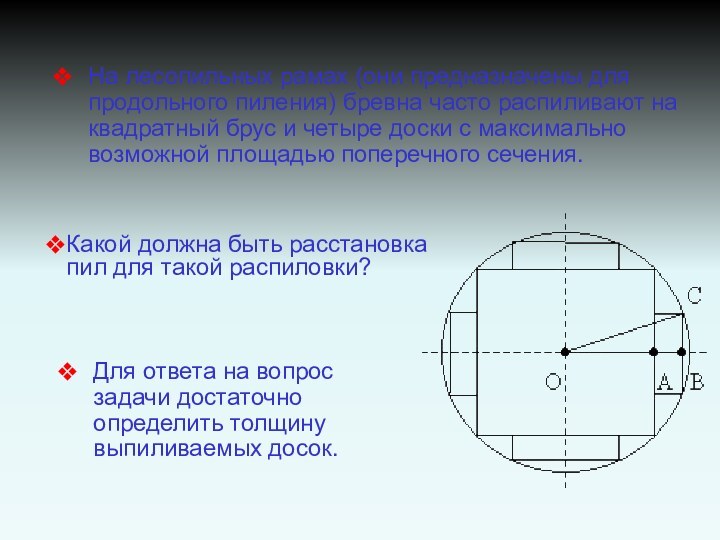
На лесопильных рамах (они предназначены для продольного пиления)
бревна часто распиливают на квадратный брус и четыре доски
с максимально возможной площадью поперечного сечения.
Для ответа на вопрос задачи достаточно определить толщину выпиливаемых досок.
Какой должна быть расстановка пил для такой распиловки?
Слайд 26
Так как сторона квадрата, вписанного в окружность радиуса
r, равна r то ОА =
Пусть
толщина доски АВ = х, тогда ее ширина 2ВС =
= , а площадь поперечного сечения:
S(x) = 2 АВ ВС = .
Требуется узнать, при каком х из
отрезка [0; ] функция S достигает наибольшего значения.
Найдем производную : S'(x) = .
Критическая точка: = Так как S(0) = S =0 , а
S( )' > 0, то доски толщиной 0,10d имеют наибольшую площадь поперечного сечения.
Ответ: 0,10d.
Слайд 27
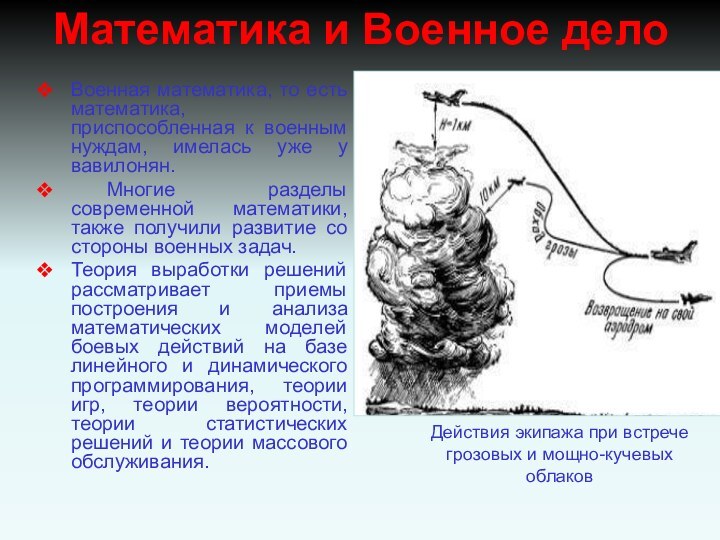
Математика и Военное дело
Военная математика, то есть математика,
приспособленная к военным нуждам, имелась уже у вавилонян.
Многие
разделы современной математики, также получили развитие со стороны военных задач.
Теория выработки решений рассматривает приемы построения и анализа математических моделей боевых действий на базе линейного и динамического программирования, теории игр, теории вероятности, теории статистических решений и теории массового обслуживания.
Действия экипажа при встрече грозовых и мощно-кучевых облаков
Слайд 28
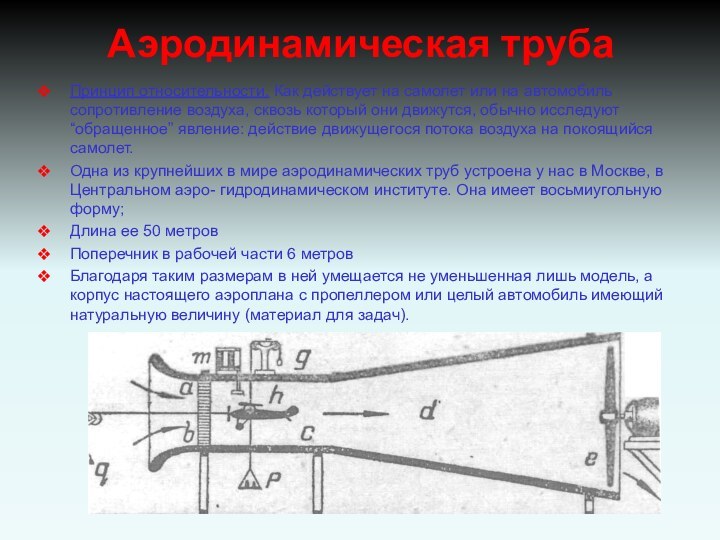
Аэродинамическая труба
Принцип относительности. Как действует на самолет или
на автомобиль сопротивление воздуха, сквозь который они движутся, обычно
исследуют “обращенное” явление: действие движущегося потока воздуха на покоящийся самолет.
Одна из крупнейших в мире аэродинамических труб устроена у нас в Москве, в Центральном аэро- гидродинамическом институте. Она имеет восьмиугольную форму;
Длина ее 50 метров
Поперечник в рабочей части 6 метров
Благодаря таким размерам в ней умещается не уменьшенная лишь модель, а корпус настоящего аэроплана с пропеллером или целый автомобиль имеющий натуральную величину (материал для задач).
Слайд 29
Отдача огнестрельного оружия
В качестве примера рассмотрим отдачу ружья.
Пороховые газы отбрасывают ружье в обратную сторону, порождая всем
известную “отдачу”. С какой скоростью движется отдающее ружьё? Чтобы ответить на этот вопрос нужно вспомнить закон равенства действия и противодействия. По этому закону давление пороховых газов на ружьё должно быть равно давлению пороховых газов на пулю. При этом обе силы действуют одинаковое время.
f t=mV
пули и для ружья одинаково, должны быть одинаковы и
количества движения. Если m- масса пули, V- её скорость, М- масса ружья, w- скорость ружья, то согласно закону мы имеем:
mV=Mw, отсюда следует:
w/V=m/М
Подставим в эту пропорцию числовые значения. Масса пули военной винтовки-0,96 кг, скорость пули при вылете- 800 м/с; масса винтовки- 4,5 кг.
w/800=0,0096/4,5
Следовательно, скорость ружья w= 1,7 м/с.
Ответ: w= 1,7 м/с.
Слайд 31
Формула механики, являющаяся математическим выражением второго закона Ньютона,
связывает силу и ускорение с массой, а не с
весом: f=ma. Но масса снаряда нисколько на Луне нe изменилась: она там та же, что и на Земле; значит, и ускорение, сообщаемое снаряду силой взрыва, должно быть на Луне такое же, как и на Земле, а при одинаковых ускорениях и времени — одинаковы и скорости (согласно формуле V=at).
Итак, пушка на Луне выбросила бы снаряд точно с такой же начальной скоростью, как и на Земле. Другое дело, как далеко или как высоко залетел бы на Луне этот снаряд.
Ответ: Снаряд на Луне покинет орудие с такой же скоростью, что и на Земле, т.е V=w= 900 м/с.
Артиллерийское орудие сообщает снаряду на Земле начальную скорость 900 м/с. С какой скоростью снаряд покинет это орудие на Луне, если известно, что на Луне все тела все тела становятся в 6 раз легче?
Пушка на луне
Слайд 32
Теперь определим давление пороховых газов. Прежде всего вычислим

силу, движущую пулю. Для этого найдем среднее ускорение движения
пули в стволе (принимая это движение за равномерно-ускоренное).
=2aS
Решение
Задача сводится к решению вопроса: какое давление на пулю больше — пороховых газов изнутри или воды океана снаружи? Последнее рассчитать несложно: каждые 10 м водяного столба давят с силой одной атмосферы, т. е. 1 кг на 1 кв. см. Следовательно, 11000 м водяного столба окажут давление в 1100 атмосфер, или больше тонны на 1 кв. см.
где V- скорость пули у дульного обреза; а- искомое ускорение; S- длина пути, пройденного пулей под непосредственным давлением газов.
Наган на дне океана
Для этой задачи взята также необычная обстановка — дно океана. Глубочайшее место океана, какое удалось промерить, находится близ Антильских островов: 11000 м.
Вообразите, что на этой глубине очутился наган и что заряд его не промок. Курок спущен, порох воспламенился. Вылетит ли пуля?
Вот сведения о нагане, необходимые для решения задачи: длина ствола 22 см; скорость пули при выходе из дула — 270 м/с; калибр (диаметр канала) — 7 мм; вес пули — 7 г.
Итак, выстрелит ли пуля из нагана на дне океана?
Слайд 33
Подставим V=270м=27000см в секунду, S= 22см, тогда
27000*27000=2а*22
a= 16500000
см/с=165 км/с
Огромная величина ускорения не должна
нас удивлять, потому что пуля проходит путь по каналу нагана в ничтожный промежуток времени, который тоже поучительно вычислить. Расчет выполняем по формуле V=at:
27000=16500000t,
t= 1/600 секунд.
Мы видим, что за 600-ю долю секунды скорость пули должна возрасти от нуля до 270 метров.
В килограмме миллион миллиграмм, значит на пулю действует сила в 115 кг. Чтобы вычислить давление надо знать, по какой площади эта сила распределяется. Площадь равна поперечному сечению канала револьвера:
¼*3,14*0,7*0,7=0,38 кв. см.
Значит на 1 кв. см. приходится давление в 115:0,38= 300кг
Итак, пуля в момент выстрела выталкивается давлением в 300 атмосфер против давления океанских вод, превышающая 1000 атмосфер. Ясно, что пуля не двинется с места. Порох вспыхнет, но не вытолкнет пулю. Пуля нагана бессильна “пробить” воду.
Слайд 34
Математические модели используются в цирке
Человек-бомба
“Человек- бомба”- номер цирковой
программы. Он состоит в том, что артист помещается в
канале пушки, выбрасывается оттуда выстрелом, описывает дугу в воздухе и падает на сетку в 30 м. от орудия.
Наклон пушки –
Наибольшая высота полета- 19м
Длина ствола пушки- 6м
Слайд 35
В первой фазе движения артиста,

которая протекает внутри пушки, нас интересует величина искусственной тяжести.
Мы узнаем ее, если вычислим ускорение тела в канале пушки. Для этого надо знать длину пушки, а также скорость, приобретаемую в конце этого пути. Длина пушки известна – 6м., скорость можно вычислить, зная, что это та скорость, с какой надо подбросить свободное тело, чтобы оно взлетело на высоту 19м. Зная формулу:
где t- продолжительность подъема вверх, V- начальная скорость, - угол, под которым брошено тело, a – ускорение. Кроме того известна высота h подъема вверх. Так как
то можно вычислить скорость V :
С такой скоростью тело артиста покидает пушку. Пользуясь формулой
имеем
Мы узнали, что это ускорение в 3,5 раза больше обычного ускорения силы тяжести. Поэтому артист будет в момент выстрела чувствовать в 4,5 раза тяжелее обычного.
Сколько времени длится ощущение усиленного веса?
Из формулы имеем
откуда
Значит, артист более полсекунды будет ощущать,
что он весит не 70 кг, а около 300кг.
Слайд 36
Перейдем ко второй фазе циркового номера – к
свободному полету артиста в воздухе. На интересует продолжительность полета;
сколько времени артист не ощущает никакого веса?
В предыдущей фазе мы установили, что продолжительность полета равна
Подставив известные нам величины узнаем, что искомая продолжительность равна:
Состояние полной невесомости длится около 4 секунд.
Слайд 37
В третьей фазе полета, определим величину искусственной тяжести

и продолжительность этого состояния. Если бы сетка находилась на
уровне жерла пушки, артист достиг бы ее с такой же скоростью, с какой начал свой полет. Но сетка поставлена несколько ниже, и оттого скорость артиста будет больше. Принимаем, что артист достиг сетки о скоростью 20,6 м/с. Далее, упав на сетку, артист вдавливает ее на 1,5 м. значит скорость 20,6 м/с превращается в нуль на пути 1,5 м. по формуле имеем
откуда ускорение
Мы узнали, что, вдавливая сетку, артист подвергается ускорению в 141 м/с - в 14 раз большему. Чем нормальное ускорение тяжести. В течение этого времени он чувствовал себя в 15 раз тяжелее нормального своего веса! Это состояние длилось всего
даже привычный организм циркача не мог бы безнаказанно перенести 15-кратное усиление тяжести, если бы это не длилось ничтожное время. Ведь человек весом 70 кг приобретает вес целой тонны! Длительность такой нагрузки должно было бы раздавить человека,
во всяком случае лишить его возможности дышать,
т.к. мускулы не смогут “поднять” столь
тяжелую грудную клетку.
Слайд 38
Заключение
Связь математики и других школьных предметов видна при
решении определенно- поставленных задач практического характера. Тем самым в
максимальной степени исполняется один из основных принципов – СВЯЗЬ НАУКИ С РЕАЛЬНОЙ ЖИЗНЬЮ.
Недостаточность задач практического содержания в учебниках по математике позволяет учителю и учащимся самостоятельно подбирать материал в соответствии с профилем обучения, тем самым преодолевается затруднение в переносе математических знаний, полученных на уроке.