Презентация на тему Текстовые задачи и моделирование

задачи на движение

задачи на производительность труда
(способы моделирования: (способы моделирования:
составление таблицы, система уравнений,
логические рассуждения составление таблицы,
схематический рисунок, сетевые графы)
решение с помощью уравнения,
сетевые графы)



задачи на растворы и смеси комбинаторные задачи
(способы моделирования: (способы моделирования:
уравнения, дерево вариантов,
логические рассуждения) правило умножения)

по реке отправляется плот. Через час из пункта А

вниз по течению отправляется катер. Найдите время , требующееся катеру, чтобы догнать плот и возвратиться в пункт А, если скорость катера в стоячей воде вдвое больше скорости течения реки.
Пусть неизвестное время – t .
V – скорость движения плота.
Так как скорости катера туда и обратно различаются в три раза, то соответствующие времена и одинаковые пути обратно пропорциональны – 1:3.
Тогда t – расстояние, пройденное катером вниз по течению;
t– расстояние, пройденное катером на обратном пути.
V + 1/4 * t *V – расстояние, пройденное плотом из А до момента, когда его догнал катер.
С другой стороны, это же расстояние, пройденное катером на обратном пути, равно 3/4 *t * V, так как его скорость движения против течения реки – V .
Приравнивая два этих выражения между собой, получаем:
V + 1/4 *t *V = 3/4 *t *V
Отсюда t=2 ч.

работе двух насосов разной мощности бассейн наполняется водой за

8 часов. После ремонта насосов производительность первого из них увеличилась в 1,2раза, а второго – в 1,6 раза, и при одновременной работе обоих насосов бассейн стал заполняться за 6 часов. За какое время наполнится бассейн при работе только первого насоса после ремонта?
Решение: В задачах на совместную работу весь объём выполняемой работы обычно принимается за единицу.
первое условие дает соотношение:
V1 + V2 = 1/8
Второе условие приводит к уравнению:
1,2V1 + 1,6V 2 =1/6
Решим систему уравнений:
v1 + v2 =1/8 1,6v1 + 1, 6v2 = 1/5
1,2v1 + 1,6v2 = 1/6 1,2v1 + 1,6v2 = 1/6 0,4v1 =1/5 -1/6 =1/30
v1 =1/12(ч)
V1 - это часть полного объема бассейна, наполняемая за 1 час первым насосом. Тогда весь бассейн будет заполнен первым насосом за 12 часов.
Ответ: 12 часов.

штукатур может выполнить задание на 5 ч быстрее другого.

Оба вместе они выполняют задание за 6 ч. За сколько часов каждый из них выполнит это задание?
Введём следующие обозначения: выполненная работа – А, время работы – t, количество работы, выполняемой за единицу времени (производительность) –k.
А = k* t, выполняемую работу, обозначим за 1.
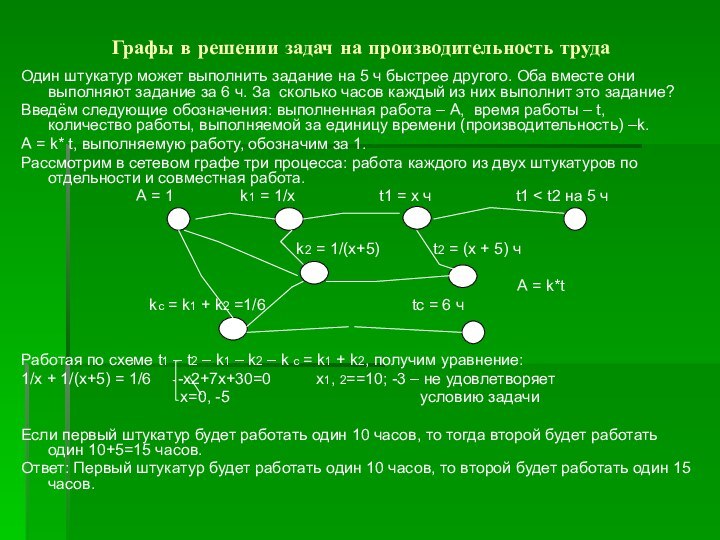
Рассмотрим в сетевом графе три процесса: работа каждого из двух штукатуров по отдельности и совместная работа.
А = 1 k1 = 1/х t1 = x ч t1 < t2 на 5 ч

k2 = 1/(х+5) t2 = (x + 5) ч

А = k*t
kc = k1 + k2 =1/6 tc = 6 ч


Работая по схеме t1 – t2 – k1 – k2 – k c = k1 + k2, получим уравнение:
1/х + 1/(х+5) = 1/6 -х2+7х+30=0 х1, 2==10; -3 – не удовлетворяет
х=0, -5 условию задачи

Если первый штукатур будет работать один 10 часов, то тогда второй будет работать один 10+5=15 часов.
Ответ: Первый штукатур будет работать один 10 часов, то второй будет работать один 15 часов.

Из бутыли, наполненной 12%-ным раствором соли, отлили 1 л

и долили бутыль водой, затем отлили еще литр и опять долили водой. В бутыли оказался 3%-ный раствор соли. Какова вместимость бутыли?
Решение с помощью выстраивания цепочки логических рассуждений:
Пусть 1/х - часть целой бутыли, которую отливали каждый раз.
Тогда после первой процедуры отливания – доливания новое процентное содержание соли – (1 – 1/х)12%;
После второй процедуры отливания – доливания процентное содержание соли – (1 – 1/х)(1 –1/х )12%, которое будет равно 3%;
Откуда получаем:
12%(1 –1/х )2 = 3%
(1 – 1/х)2 = 1/4
1/х= 1/2,
значит, каждый раз отливалась половина бутыли
Следовательно, объем бутыли равен 2 л.
Ответ: 2 л.

качестве символа своего государства решили использовать флаг в

виде четырех вертикальных полос, одинаковых по ширине, но разных по цвету: белый, синий, красный, зеленый. У каждой страны свой, отличный от других, флаг. Сколько всего стран могут использовать такую символику?
Решение:
составим дерево вариантов для одной ветви, где первая полоса – белая:
Первая полоса Б С К З
Вторая полоса С К З

Третья полоса К З С З С К

Четвертая полоса З К З С К С

Ветви для остальных трёх первых полос будут аналогичными. Анализ первой ветви показывает, что с первой белой полосой можно составить 6 различных флагов. Следовательно по столько флагов будет с первой синей, красной и зелёной полосами. По правилу умножения получаем: 6*4=24 флага.
Ответ: 24 флага.