изучить свойства соответствий для применения в задачах компьютерной инженерии
Содержание:
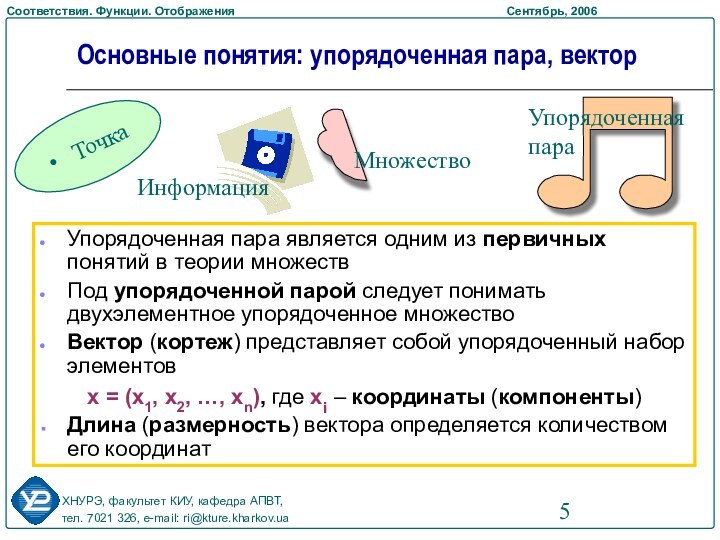
Понятие упорядоченной пары и вектора
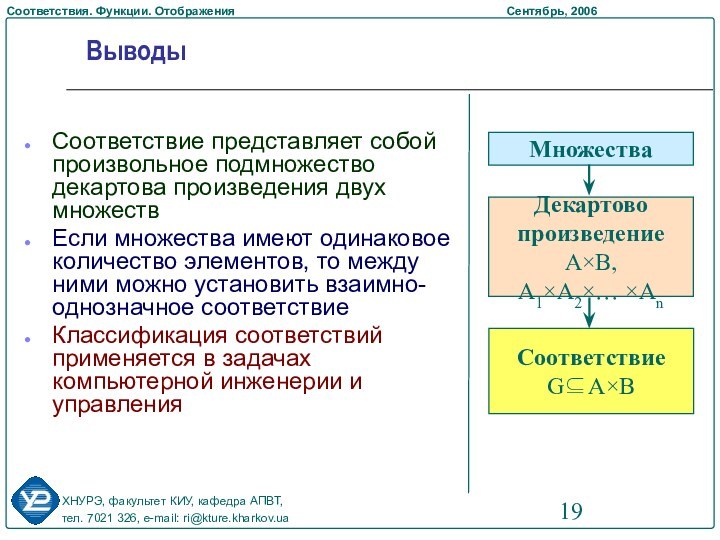
Декартово произведение множеств
Определение соответствия
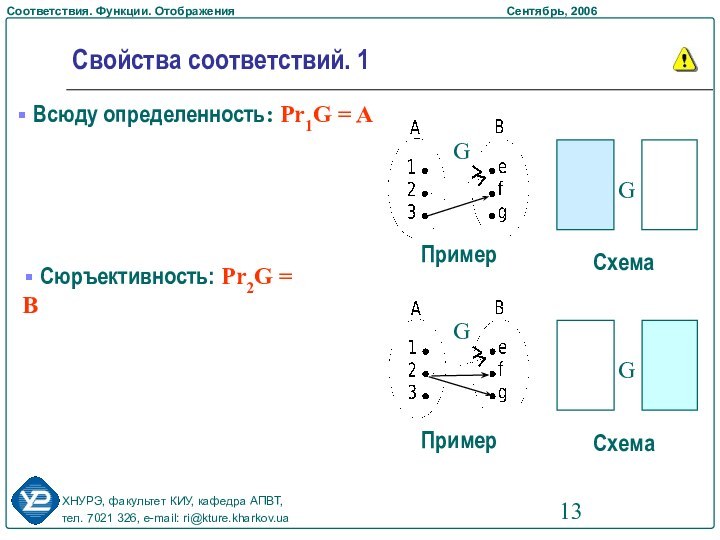
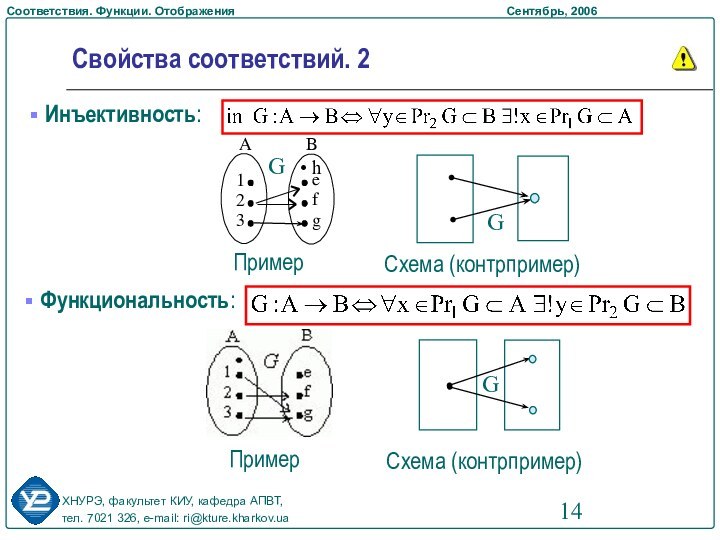
Свойства соответствий
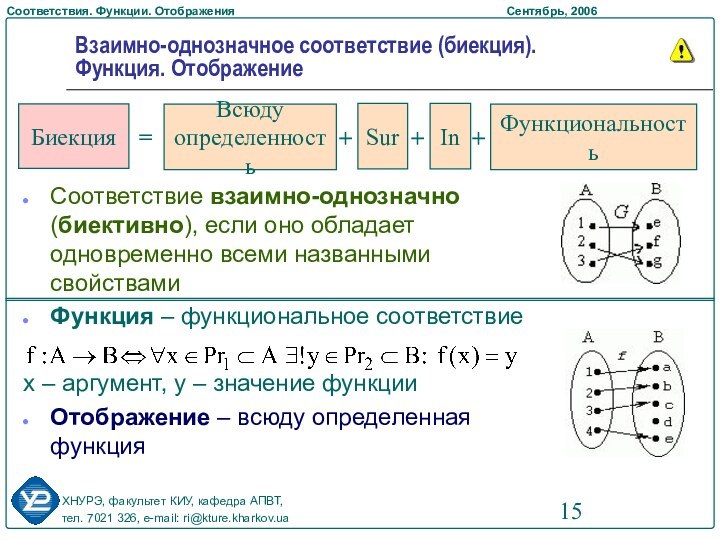
Взаимно-однозначное соответствие
Функции
Отображения
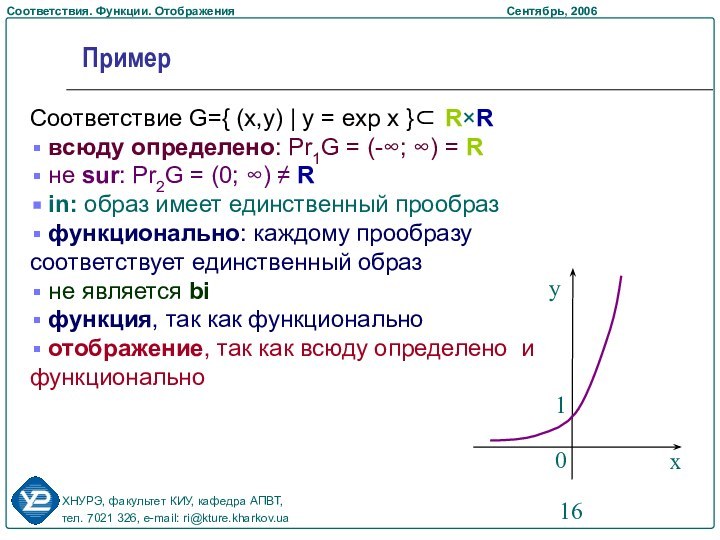
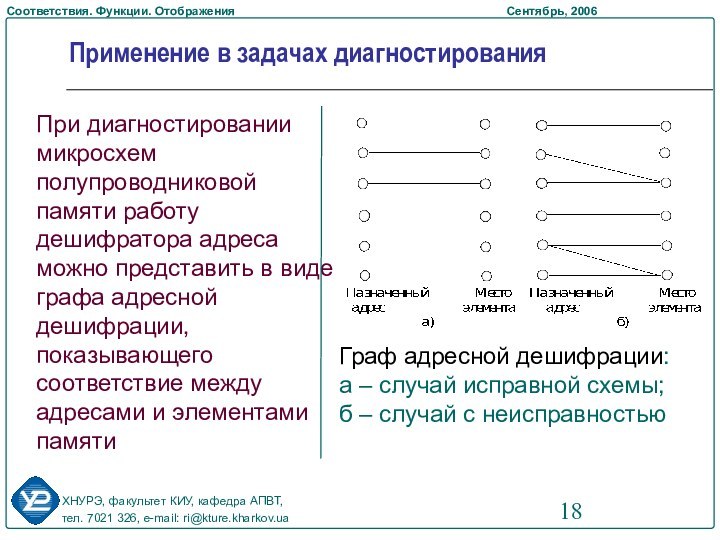
Примеры применения в теории кодирования и задачах диагностирования
Тема: Соответствия. Функции. Отображения