- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Тождественные преобразования тригонометрических выражений
Содержание
- 2. Основные понятиятригонометрическая окружность градусы и радианысинус и косинустангенс и котангенс
- 3. Тригонометрическая окружность0xyIIIIIIIV
- 4. Градусы и радианы0xy
- 5. Градусы и радианы0xy
- 6. Градусы и радианы
- 7. Перевод из радиан в градусыЧтобы найти радианную
- 8. Пример 1.Найти радианную меру угла 12°30’ с
- 9. Из градусов в радианыЧтобы найти градусную меру
- 10. Пример 2.Найти градусную меру угла 1.4 рад
- 11. Пример 2 (продолжение)Таким образом, 0.4 рад 22°55’6”
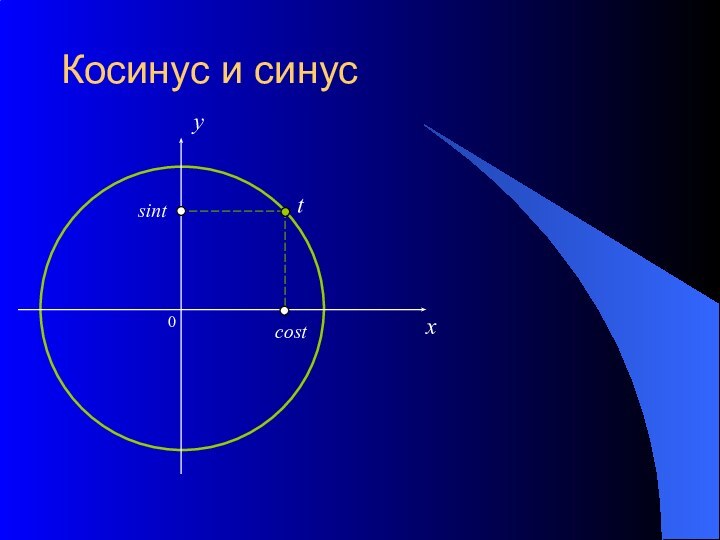
- 12. Косинус и синус0xycostsintt
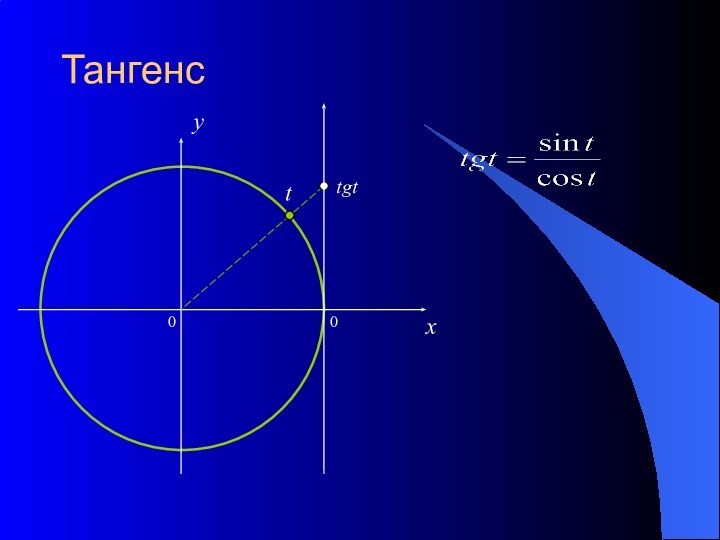
- 13. Тангенс0xytgtt0
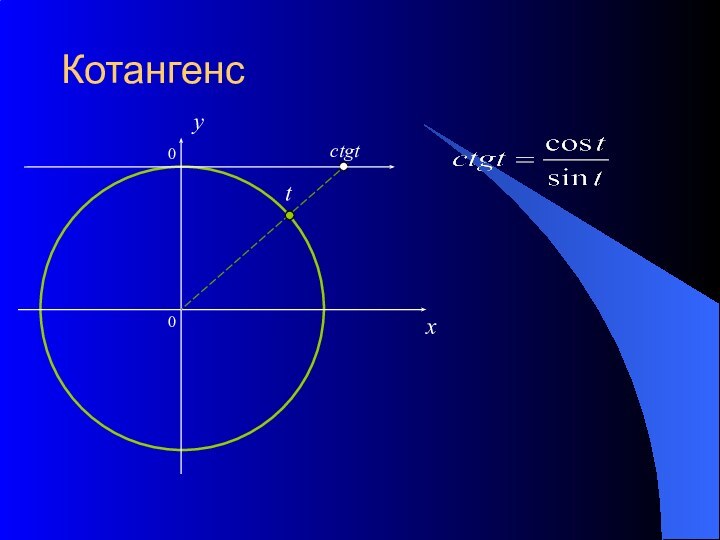
- 14. Котангенс0xyctgtt0
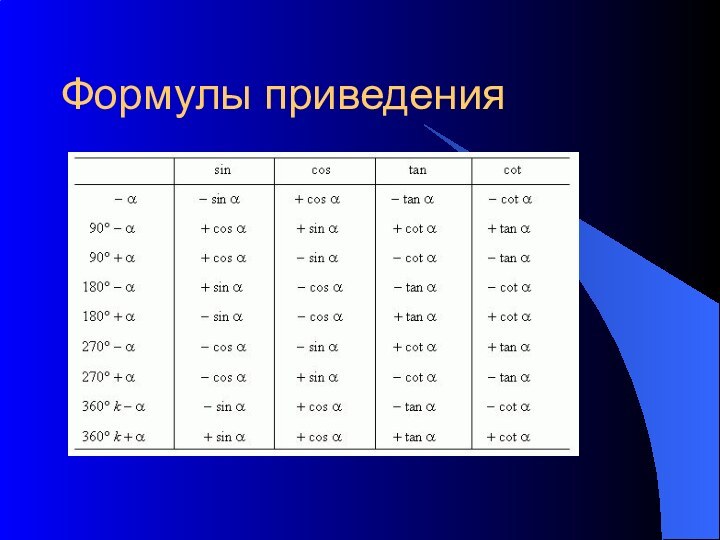
- 15. Формулы приведенияЭти формулы позволяют: 1) найти
- 16. Формулы приведения
- 17. Соотношения между тригоно-мерическими функциями одного и того же угла
- 18. Формулы сложения и вычитания
- 19. Формулы двойных, тройных и половинных углов
- 20. Преобразо-вание триго-нометрических выражений в произведение
- 21. Преобразование тригоно-метрических выражений в произведение
- 22. Обратные тригонометрические функции arcsin x – это
- 23. Обратные тригонометрические функции Если обозначить любое из
- 24. Скачать презентацию
- 25. Похожие презентации
Основные понятиятригонометрическая окружность градусы и радианысинус и косинустангенс и котангенс




















Слайд 2
Основные понятия
тригонометрическая окружность
градусы и радианы
синус и косинус
тангенс
и котангенс
Слайд 7
Перевод из радиан в градусы
Чтобы найти радианную меру
любого угла по его данной градусной мере, надо умножить
число градусов на / 180 0.017453, число минут – на / ( 180 · 60 ) 0.000291, число секунд – на / ( 180 · 60 · 60 ) 0.000005 и сложить найденные произведения.
Слайд 8
Пример 1.
Найти радианную меру угла 12°30’ с точностью
до четвёртого десятичного знака.
Р е ш е н и
е . Умножим 12 на / 180 : 12 · 0.017453 0.2094.
Умножим 30 на / (180 · 60 ) : 30 ·
· 0.000291 0.0087.
Теперь находим:
12°30’ 0.2094 + 0.0087 = 0.2181 рад.
Слайд 9
Из градусов в радианы
Чтобы найти градусную меру любого
угла по его данной радианной мере, надо умножить число
радиан на 180° / 57°.296 = 57°17’45” (относительная погрешность результата составит ~ 0.0004%, что соответствует абсолютной погрешности ~ 5” для полного оборота 360° ).
Слайд 10
Пример 2.
Найти градусную меру угла 1.4 рад с
точностью до 1’.
Р е ш е н и
е . Последовательно найдём:
1 рад 57°17’45” ;
0.4 рад 0.4 · 57°.296 = 22°.9184;
0°.9184 · 60 55’.104; 0’.104 · 60 6”.
…
Слайд 11
Пример 2 (продолжение)
Таким образом, 0.4 рад 22°55’6” и
тогда:
1 рад 57°17’45”
+
0.4 рад 22°55’6”
___________________________
1.4 рад 80°12’51”После округления этого результата до требуемой точности в 1’ окончательно получим: 1.4 рад » 80°13’.
Слайд 15
Формулы приведения
Эти формулы позволяют:
1) найти численные
значения тригонометрических функций углов, больших 90°;
2) выполнить преобразования, приводящие
к более простым выражениям;3) избавиться от отрицательных углов и углов, больших 360°.
Слайд 22
Обратные тригонометрические функции
arcsin x – это угол, синус
которого равен x. Аналогично определяются функции arccos x, arctan
x, arccot x, arcsec x, arccosec x. Эти функции являются обратными по отношению к функциям sin x, cos x, tan x, cot x, sec x, cosec x, поэтому они называются обратными тригонометрическими функциями. Все обратные тригонометрические функции являются многозначными функциями, то есть каждому значению аргумента соответствует бесчисленное множество значений функции. Так, например, углы 30°, 150°, 390°, 510°, 750° имеют один и тот же синус.
Слайд 23
Обратные тригонометрические функции
Если обозначить любое из значений обратных
тригонометрических функций через Arcsin x, Arccos x, Arctan x,
Arccot x и сохранить обозначения: arcsin x, arcos x, arctan x, arccot x для их главных значений, то связь между ними выражается следующими соотношениями:где k – любое целое число. При k = 0 мы имеем главные значения.