- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Трапеция. Теорема о средней линии трапеции
Содержание
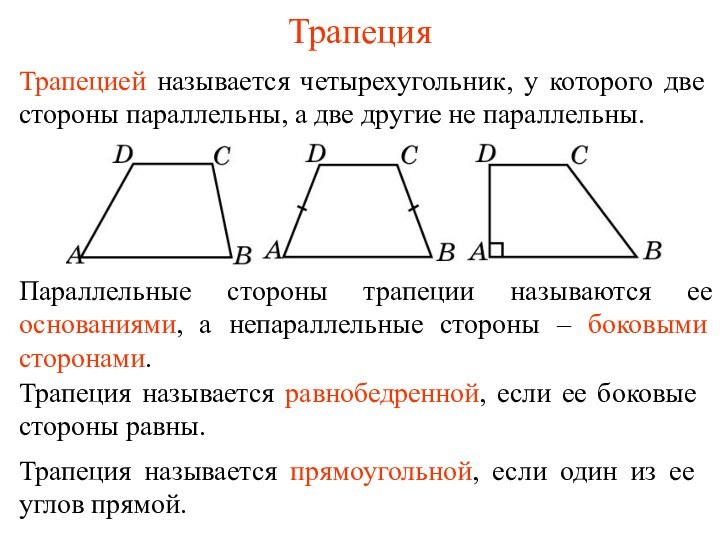
- 2. Средняя линия трапецииСредней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
- 3. Теорема о средней линии трапецииТеорема. Средняя линия
- 4. Вопрос 1Какой четырехугольник называется трапецией?Ответ: Трапецией называется
- 5. Вопрос 2Какие стороны трапеции называются: а) основаниями;
- 6. Вопрос 3Какая трапеция называется: а) равнобедренной; б)
- 7. Вопрос 4Что называется средней линией трапеции? Ответ:
- 8. Вопрос 5Сформулируйте теорему о средней линии трапеции.Ответ: Средняя линия трапеции параллельна основаниям и равна их полусумме.
- 9. Упражнение 1Изобразите равнобедренную трапецию ABCD, три вершины
- 10. Упражнение 2Изобразите прямоугольную трапецию ABCD, три вершины
- 11. Упражнение 3Могут ли углы, прилежащие к основанию трапеции, быть один острым, а другой тупым?
- 12. Упражнение 4Может ли у трапеции быть: а)
- 13. Упражнение 5Докажите, что углы при основании равнобедренной
- 14. Упражнение 6Верно ли, что если два угла
- 15. Упражнение 7Верно ли, что если два угла при основании трапеции равны, то она равнобедренная?Ответ. Да.
- 16. Упражнение 8Докажите, что сумма двух противоположных углов
- 17. Упражнение 9Чему равны углы равнобедренной трапеции, если
- 18. Упражнение 10Докажите, что диагонали равнобедренной трапеции равны.
- 19. Упражнение 11Верно ли, что если диагонали трапеции равны, то она равнобедренная?Ответ. Да.
- 20. Упражнение 12Определите вид четырехугольника, который получится, если последовательно соединить отрезками середины сторон равнобедренной трапеции.
- 21. Упражнение 13Прямая, проведенная параллельно боковой стороне трапеции
- 22. Упражнение 14Проведите среднюю линию трапеции, изображенной на рисунке.
- 23. Упражнение 15Проведите среднюю линию трапеции, изображенной на рисунке.
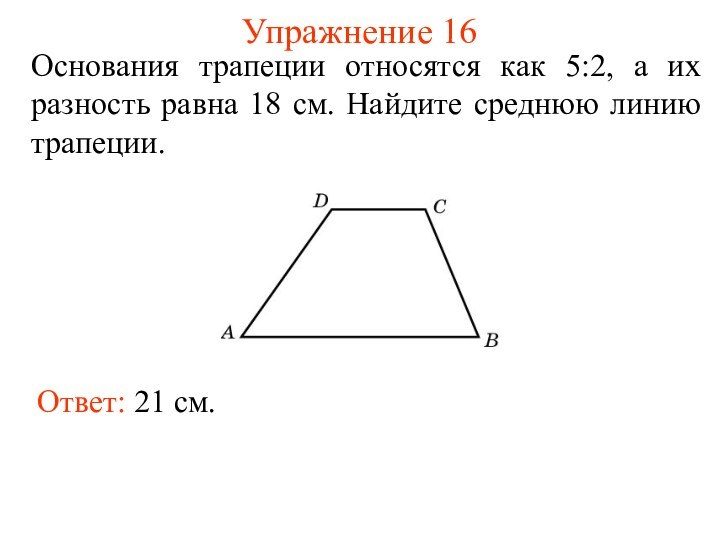
- 24. Упражнение 16Основания трапеции относятся как 5:2, а
- 25. Упражнение 17Периметр трапеции равен 50 см, а
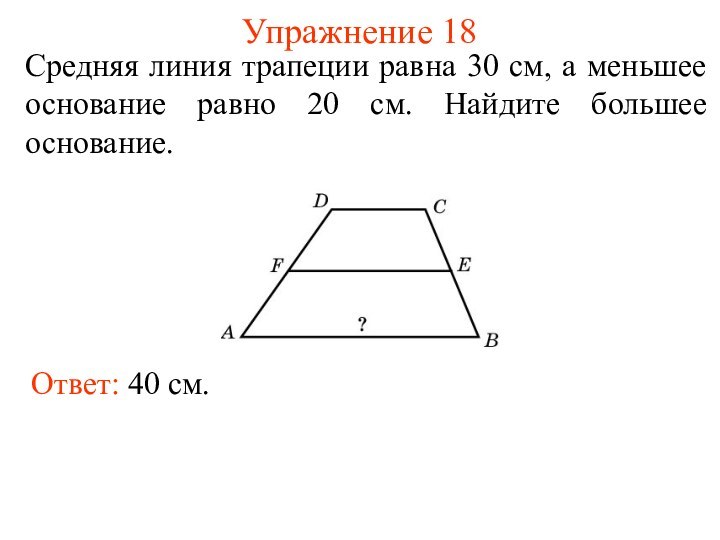
- 26. Упражнение 18Средняя линия трапеции равна 30 см,
- 27. Упражнение 19Периметр равнобедренной трапеции равен 80 см,
- 28. Упражнение 20Средняя линия трапеции равна 7 см,
- 29. Упражнение 21Основания трапеции относятся как 2 :
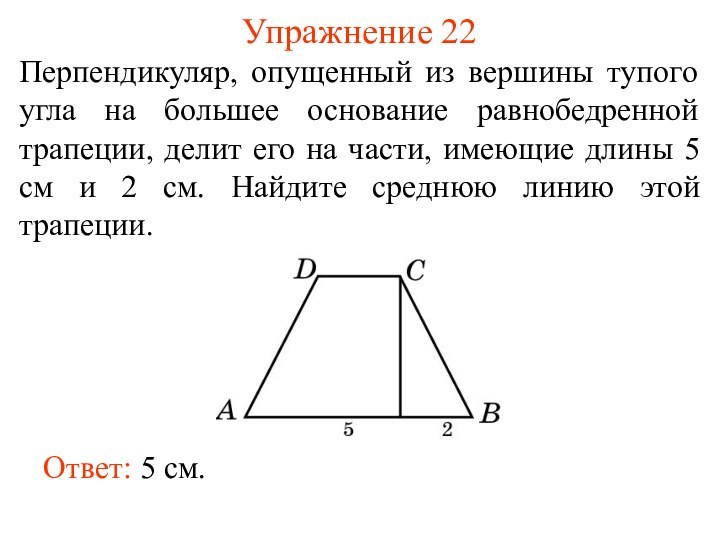
- 30. Упражнение 22Перпендикуляр, опущенный из вершины тупого угла
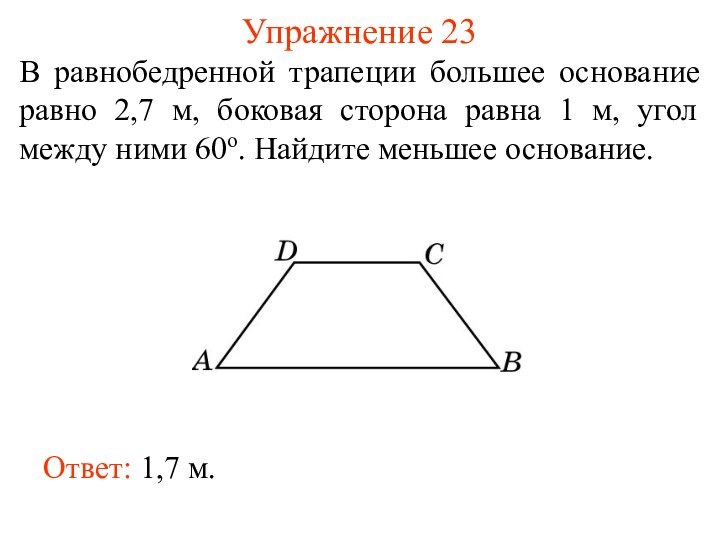
- 31. Упражнение 23В равнобедренной трапеции большее основание равно
- 32. Упражнение 24Cредняя линия трапеции равна 10 см.
- 33. Упражнение 25Основания трапеции равны 4 см и
- 34. Упражнение 26Меньшее основание равнобедренной трапеции равно боковой
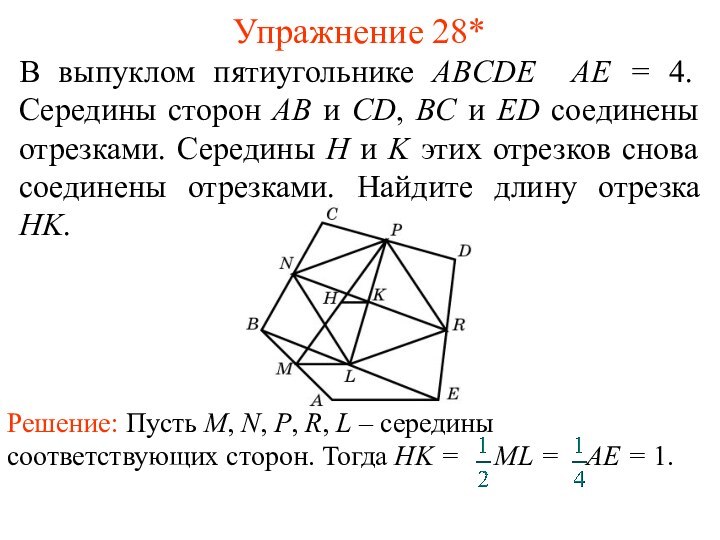
- 35. Упражнение 27*Может ли средняя линия трапеции пройти через точку пересечения диагоналей?
- 36. Скачать презентацию
- 37. Похожие презентации




























Слайд 2
Средняя линия трапеции
Средней линией трапеции называется отрезок, соединяющий
середины ее боковых сторон.
Слайд 3
Теорема о средней линии трапеции
Теорема. Средняя линия трапеции
параллельна основаниям и равна их полусумме.
Доказательство. Пусть EF –
средняя линия трапеции ABCD (AB || CD). Проведем прямую DF и ее точку пересечения с прямой AB обозначим G. Треугольники DFC и GFB равны по второму признаку равенства треугольников (CF = BF по условию, угол 1 равен углу 2, как вертикальные, угол 3 равен углу 4, как накрест лежащие углы). Из равенства этих треугольников следует, что DF = GF и, значит, EF - средняя линия треугольника AGD. Из теоремы о средней линии треугольника следует, что EF параллельна AB и EF = AG. Так как AB || CD, то EF будет параллельна обоим основаниям и кроме того, EF = AG/2 = (AB + BG)/2 = (AB + CD)/2.
Слайд 4
Вопрос 1
Какой четырехугольник называется трапецией?
Ответ: Трапецией называется четырехугольник,
у которого две стороны параллельны, а две другие не
параллельны.
Слайд 5
Вопрос 2
Какие стороны трапеции называются: а) основаниями; б)
боковыми сторонами?
Ответ: а) Основаниями трапеции называются ее параллельные стороны;
б) боковыми сторонами трапеции называются ее непараллельные стороны.
Слайд 6
Вопрос 3
Какая трапеция называется: а) равнобедренной; б) прямоугольной?
Ответ: а) Трапеция называется равнобедренной, если ее боковые стороны
равны; б) трапеция называется прямоугольной, если один из ее углов прямой.
Слайд 7
Вопрос 4
Что называется средней линией трапеции?
Ответ: Средней
линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
Слайд 8
Вопрос 5
Сформулируйте теорему о средней линии трапеции.
Ответ: Средняя
линия трапеции параллельна основаниям и равна их полусумме.
Слайд 9
Упражнение 1
Изобразите равнобедренную трапецию ABCD, три вершины которой
даны на рисунке, а четвертая находится в одном из
узлов сетки.
Слайд 10
Упражнение 2
Изобразите прямоугольную трапецию ABCD, три вершины которой
даны на рисунке, а четвертая находится в одном из
узлов сетки.
Слайд 11
Упражнение 3
Могут ли углы, прилежащие к основанию трапеции,
быть один острым, а другой тупым?
Слайд 12
Упражнение 4
Может ли у трапеции быть: а) три
прямых угла; б) три острых угла?
Ответ: а) Нет;
б) нет.
Слайд 13
Упражнение 5
Докажите, что углы при основании равнобедренной трапеции
равны.
Доказательство. Пусть ABCD – трапеция, AD не параллельна
BC. Докажем, что углы A и B равны.Через вершину C проведем прямую, параллельную AD и обозначим E ее точку пересечения с прямой AB.
Четырехугольник AECD – параллелограмм, следовательно, угол BAD равен углу BEC. Треугольник BCE – равнобедренный, следовательно, угол BCE равен углу BEC. Таким образом, в трапеции ABCD угол A равен углу B.
Слайд 14
Упражнение 6
Верно ли, что если два угла трапеции
равны, то она равнобедренная?
Ответ. Нет, она может быть прямоугольной.
Слайд 15
Упражнение 7
Верно ли, что если два угла при
основании трапеции равны, то она равнобедренная?
Ответ. Да.
Слайд 16
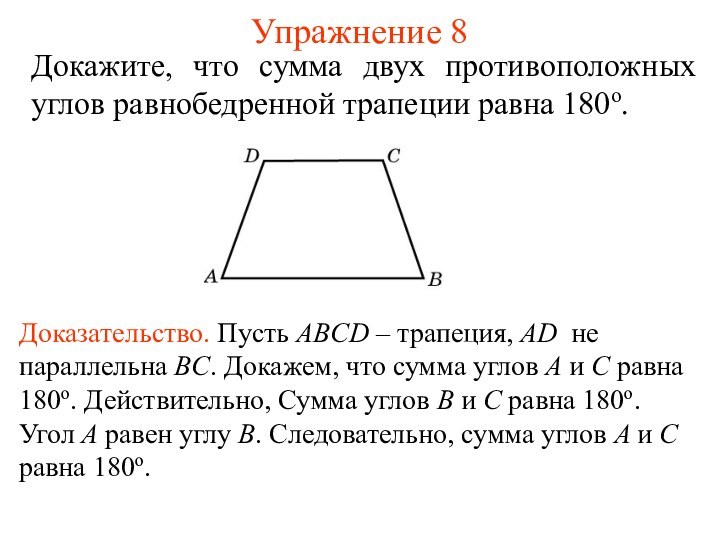
Упражнение 8
Докажите, что сумма двух противоположных углов равнобедренной
трапеции равна 180о.
Доказательство. Пусть ABCD – трапеция, AD
не параллельна BC. Докажем, что сумма углов A и С равна 180о. Действительно, Сумма углов B и C равна 180о. Угол A равен углу B. Следовательно, сумма углов A и С равна 180о.
Слайд 17
Упражнение 9
Чему равны углы равнобедренной трапеции, если известно,
что разность противолежащих углов равна 40о?
Ответ: 70о, 110о, 70о,
110о.
Слайд 18
Упражнение 10
Докажите, что диагонали равнобедренной трапеции равны.
Доказательство.
Пусть ABCD – равнобедренная трапеция. Треугольники ABC и BAD
равны (AB – общая сторона, BC = AD, угол ABC равен углу BAD. Следовательно, AC = BD.
Слайд 20
Упражнение 12
Определите вид четырехугольника, который получится, если последовательно
соединить отрезками середины сторон равнобедренной трапеции.
Слайд 21
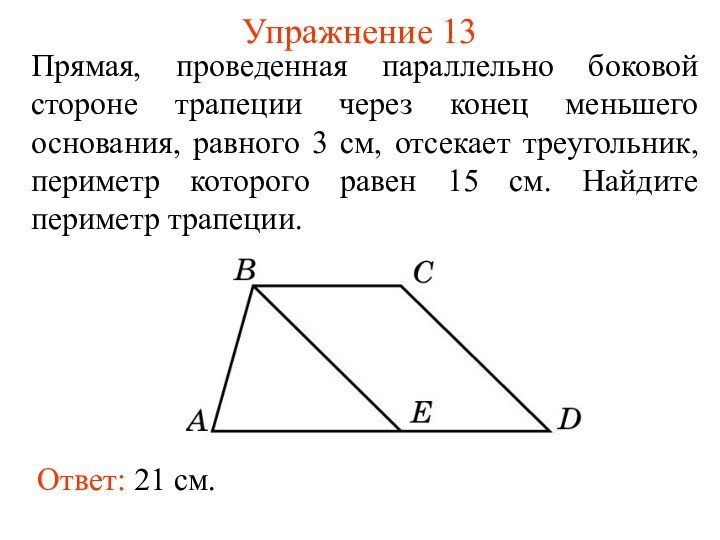
Упражнение 13
Прямая, проведенная параллельно боковой стороне трапеции через
конец меньшего основания, равного 3 см, отсекает треугольник, периметр
которого равен 15 см. Найдите периметр трапеции.Ответ: 21 см.
Слайд 24
Упражнение 16
Основания трапеции относятся как 5:2, а их
разность равна 18 см. Найдите среднюю линию трапеции.
Ответ:
21 см.
Слайд 25
Упражнение 17
Периметр трапеции равен 50 см, а сумма
непараллельных сторон равна 20 см. Найдите среднюю линию трапеции.
Ответ:
15 см.
Слайд 26
Упражнение 18
Средняя линия трапеции равна 30 см, а
меньшее основание равно 20 см. Найдите большее основание.
Ответ: 40
см.
Слайд 27
Упражнение 19
Периметр равнобедренной трапеции равен 80 см, ее
средняя линия равна боковой стороне. Найдите боковую сторону данной
трапеции.Ответ: 20 см.
Слайд 28
Упражнение 20
Средняя линия трапеции равна 7 см, а
одно из ее оснований больше другого на 4 см.
Найдите основания трапеции.Ответ: 5 см и 9 см.
Слайд 29
Упражнение 21
Основания трапеции относятся как 2 : 3,
а средняя линия равна 5 м. Найдите основания.
Ответ: 4
м и 6 м.
Слайд 30
Упражнение 22
Перпендикуляр, опущенный из вершины тупого угла на
большее основание равнобедренной трапеции, делит его на части, имеющие
длины 5 см и 2 см. Найдите среднюю линию этой трапеции.Ответ: 5 см.
Слайд 31
Упражнение 23
В равнобедренной трапеции большее основание равно 2,7
м, боковая сторона равна 1 м, угол между ними
60о. Найдите меньшее основание.Ответ: 1,7 м.
Слайд 32
Упражнение 24
Cредняя линия трапеции равна 10 см. Одна
из диагоналей делит ее на два отрезка, разность которых
равна 2 см. Найдите основания этой трапеции.Ответ: 8 см и 12 см.
Слайд 33
Упражнение 25
Основания трапеции равны 4 см и 10
см. Найдите отрезки, на которые делит среднюю линию этой
трапеции одна из ее диагоналей.Ответ: 2 см и 5 см.