- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Цилиндр (11 класс)
Содержание
- 2. Введение.Основная часть.Что называют цилиндром? (из истории).Различные определения.Выпуклый
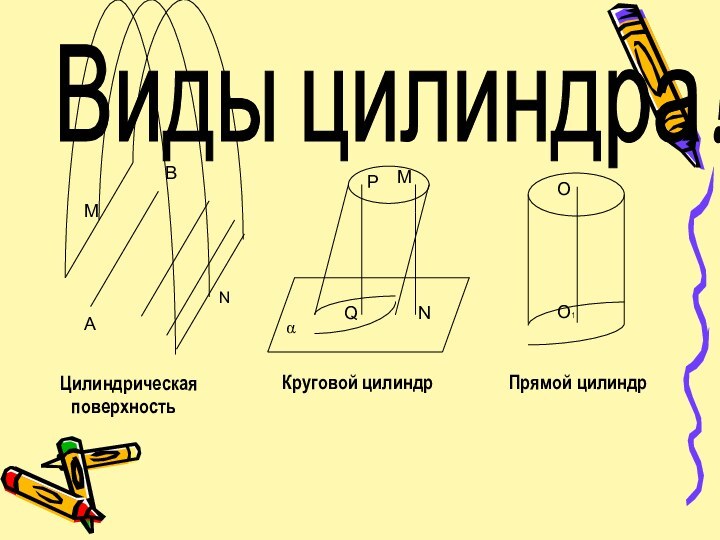
- 3. Виды цилиндра! Цилиндрическая поверхностьКруговой цилиндрПрямой цилиндр
- 4. Свойства цилиндра.1) Основания равны и параллельны 2)
- 5. Сечения цилиндра.1) Если секущая плоскость проходит через
- 6. Эллипс как сечение цилиндра.Если боковую поверхность цилиндра
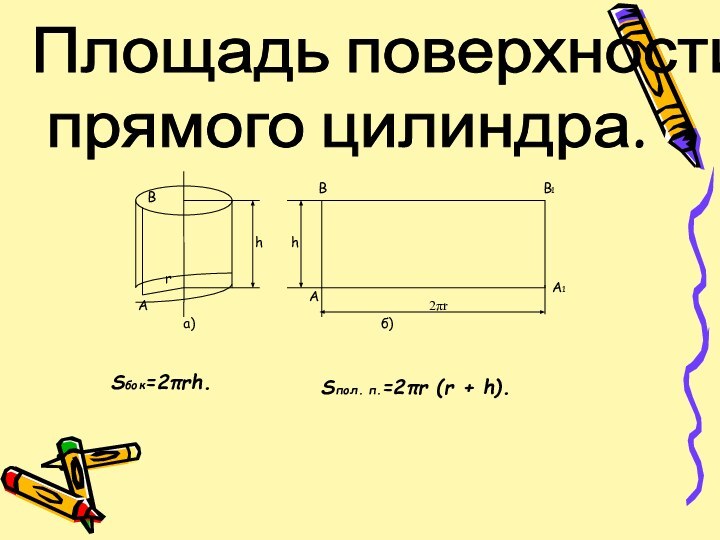
- 7. Площадь поверхности прямого цилиндра. Sбок=2πrh.Sпол. п.=2πr (r + h).
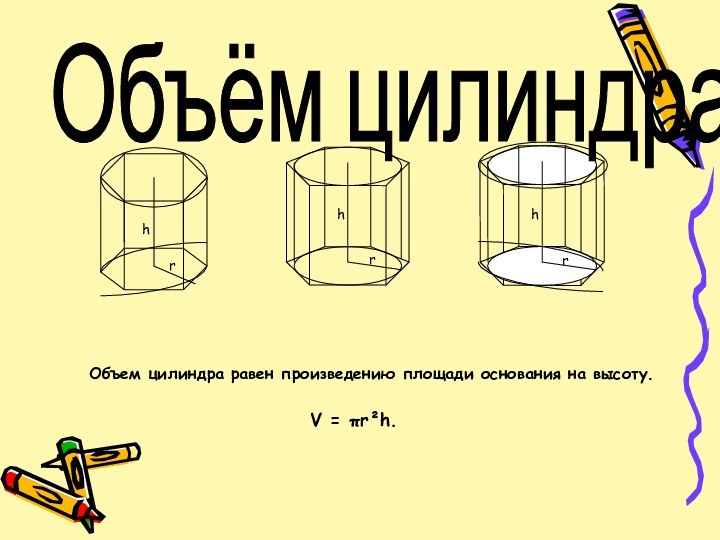
- 8. Объём цилиндра.Объем цилиндра равен произведению площади основания на высоту.V = πr²h.
- 9. Решение задач.Высота цилиндра равна Н, радиус его
- 10. Решение задач.Высота цилиндра равна 12 см. Через
- 11. Скачать презентацию
- 12. Похожие презентации





Слайд 2
Введение.
Основная часть.
Что называют цилиндром? (из истории).
Различные определения.
Выпуклый цилиндр.
Свойства
цилиндра.
Слайд 4
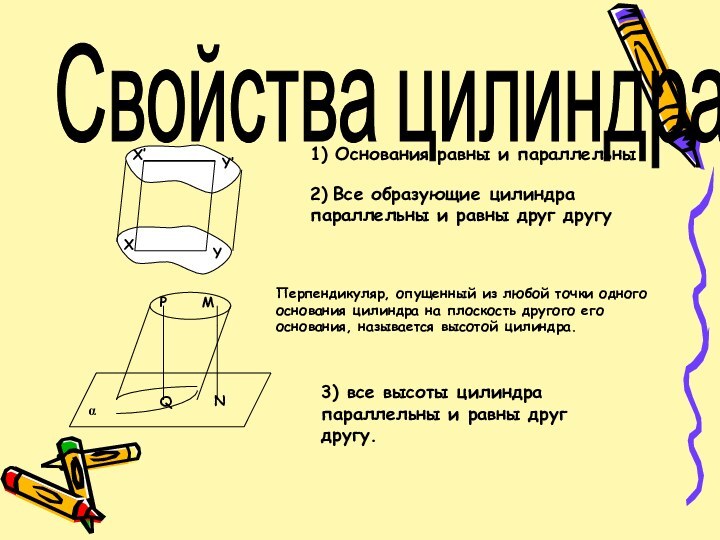
Свойства цилиндра.
1) Основания равны и параллельны
2) Все
образующие цилиндра параллельны и равны друг другу
3) все
высоты цилиндра параллельны и равны друг другу. Перпендикуляр, опущенный из любой точки одного основания цилиндра на плоскость другого его основания, называется высотой цилиндра.
Слайд 5
Сечения цилиндра.
1) Если секущая плоскость проходит через ось
цилиндра, то сечение представляет собой прямоугольник , две стороны
которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым.2) Все сечения цилиндра плоскостями параллельными плоскости основания, равны основаниям цилиндра между собой.
Слайд 6
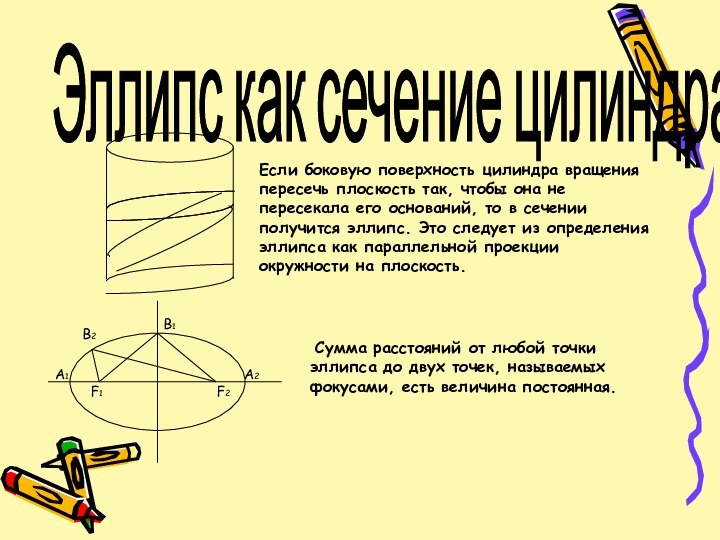
Эллипс как сечение цилиндра.
Если боковую поверхность цилиндра вращения
пересечь плоскость так, чтобы она не пересекала его оснований,
то в сечении получится эллипс. Это следует из определения эллипса как параллельной проекции окружности на плоскость. Сумма расстояний от любой точки эллипса до двух точек, называемых фокусами, есть величина постоянная.
Слайд 9
Решение задач.
Высота цилиндра равна Н, радиус его основания
равен R. В цилиндр помещена пирамида, высота которой совпадает
с образующей АА1 цилиндра, а основанием служит равнобедренный треугольник АВС (АВ=АС), вписанный в основание цилиндра. Найти площадь боковой поверхности пирамиды, если А = 120°.Дано: цилиндр с высотой H и радиусом R, вписана пирамида, образующая АА1 – высота пирамиды, АВС р/б, АВ=АС, АВС – вписан в основание цилиндра,
угол А = 120°.
Найти: Sбок пирамиды.
Решение:
1)Проведем AD ┴ BC и соединим точки А1 и D. Согласно теореме , имеем А1D┴ BC. Так
как дуга CAB содержит 120° , а дуги АС и АВ – по 60° , то ВС = R , АВ = R .
2)В ∆ ABD имеем AD = R/2 . Далее, из ∆AA1D получим
A1D = ½
Следовательно SА1АВ = ½ АВ · АА1 = ½ RH
SА1ВС = ½ ВС · А1D = ½ R ∙ ½ = ¼ R
3) Sбок = 2 SА1АВ + SА1ВС = RH + ¼ R =
= R/4(4H + ).
Ответ: R/4(4H + ).
Слайд 10
Решение задач.
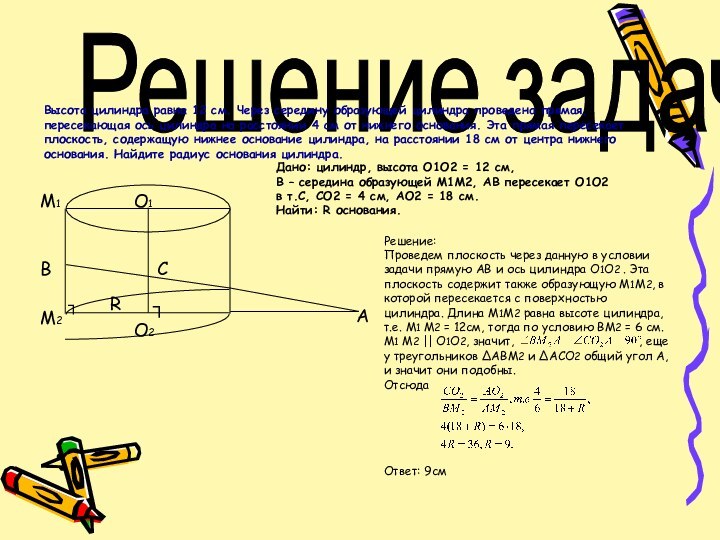
Высота цилиндра равна 12 см. Через середину
образующей цилиндра проведена прямая, пересекающая ось цилиндра на расстоянии
4 см от нижнего основания. Эта прямая пересекает плоскость, содержащую нижнее основание цилиндра, на расстоянии 18 см от центра нижнего основания. Найдите радиус основания цилиндра.Дано: цилиндр, высота О1О2 = 12 см,
В – середина образующей М1М2, АВ пересекает О1О2 в т.С, СО2 = 4 см, АО2 = 18 см.
Найти: R основания.