Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Цилиндр

Содержание

2. Цилиндр Цилиндром называется тело, которое состоит
3. Поверхность цилиндра состоит из оснований
4. Цилиндр называется прямым, если его
5. Радиусом цилиндра называется радиус его основанияRR
6. Высотой цилиндра называется расстояние между плоскостями основанийН
7. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим.RR
8. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением
9. Цилиндр, осевое сечение, которого-квадрат называется равносторонним
10. Плоскость, перпендикулярная оси цилиндра, пересекает
11. Плоскость, проходящая через образующую цилиндра
12. Задача № 1 Высота цилиндра 8
13. Решение:
14. 1)Сечение АВВ'А' - квадрат2) Фигура OAВO'A' В'-
15. Задача № 2В цилиндр вписана правильная шестиугольная
16. Решение:
17. 1. Боковые грани призмы - квадраты, так
18. Задача № 3 Сережа насыпал в
19. Решение:
20. На рисунке слева изображена
21. Эта величина не зависит от размеров цилиндра( кастрюли)
22. Цилиндры в моей профессии
27. Скачать презентацию
28. Похожие презентации

Цилиндр Цилиндром называется тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих круговА1ВАВ1

Проект «Математика в профессии «Повар, кондитер» Автор: преподаватель ГОУ СПО ПК № 33Симоненко Е.Е.

Поверхность цилиндра состоит из оснований цилиндра – двух равных кругов,

Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований. Прямой

Радиусом цилиндра называется радиус его основанияRR

Высотой цилиндра называется расстояние между плоскостями основанийН

Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим.RR

Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением

Цилиндр, осевое сечение, которого-квадрат называется равносторонним

Плоскость, перпендикулярная оси цилиндра, пересекает его боковую поверхность по окружности,

Плоскость, проходящая через образующую цилиндра и перпендикулярна осевому сечению, проведённому

Задача № 1 Высота цилиндра 8 м, радиус основания 5 м.

1)Сечение АВВ'А' - квадрат2) Фигура OAВO'A' В'- прямая треугольная призма, в которой

Задача № 2В цилиндр вписана правильная шестиугольная призма. Найдите угол между диагональю

1. Боковые грани призмы - квадраты, так как сторона правильного шестиугольника, вписанного

Задача № 3 Сережа насыпал в цилиндрическую кастрюлю немного пшена и

На рисунке слева изображена стоящая кастрюля, а на рисунке

Эта величина не зависит от размеров цилиндра( кастрюли)

Слайды презентации

Слайд 2 Цилиндр
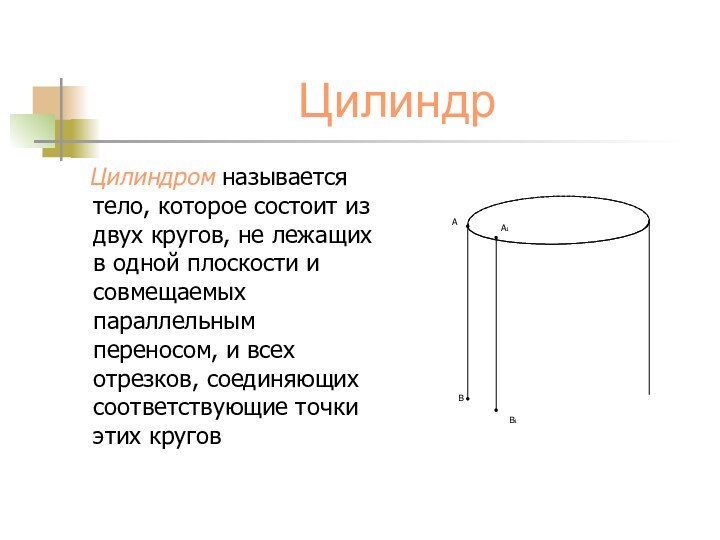
Цилиндром называется тело, которое состоит из

двух кругов, не лежащих в одной плоскости и совмещаемых

параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов

А1

В1

Слайд 3 Поверхность цилиндра состоит из оснований цилиндра

– двух равных кругов, лежащих в параллельных плоскостях, и

боковой поверхности.

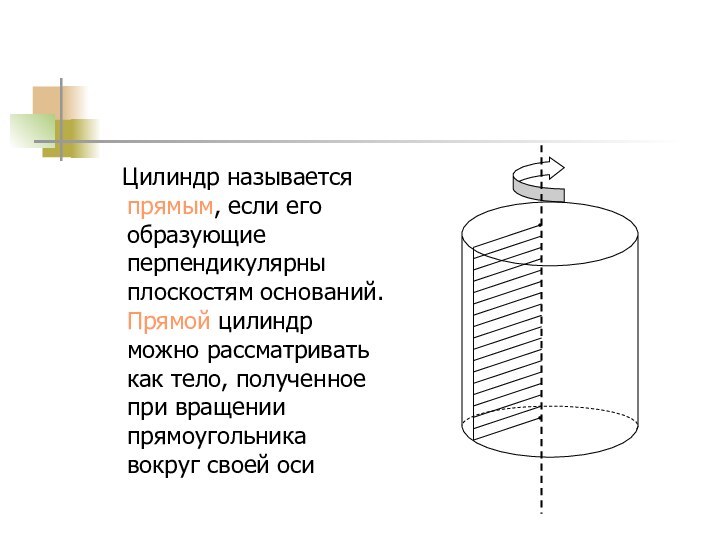
Слайд 4 Цилиндр называется прямым, если его образующие

перпендикулярны плоскостям оснований. Прямой цилиндр можно рассматривать как тело,

полученное при вращении прямоугольника вокруг своей оси

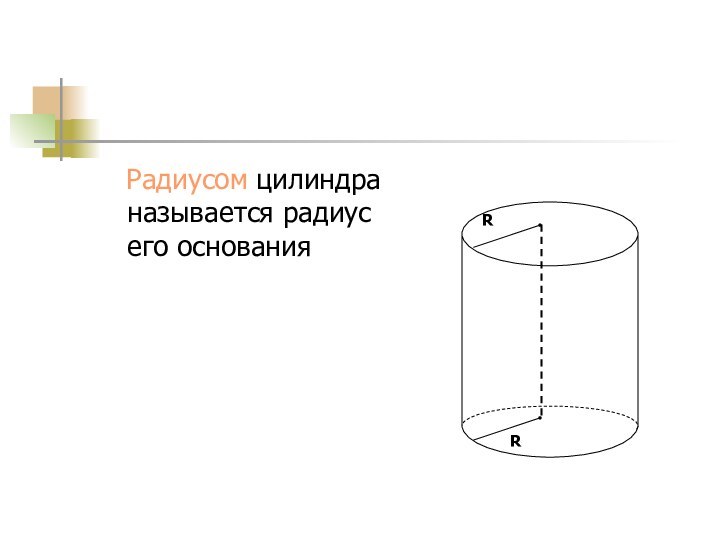
Слайд 5 Радиусом цилиндра называется радиус его основания
R
R

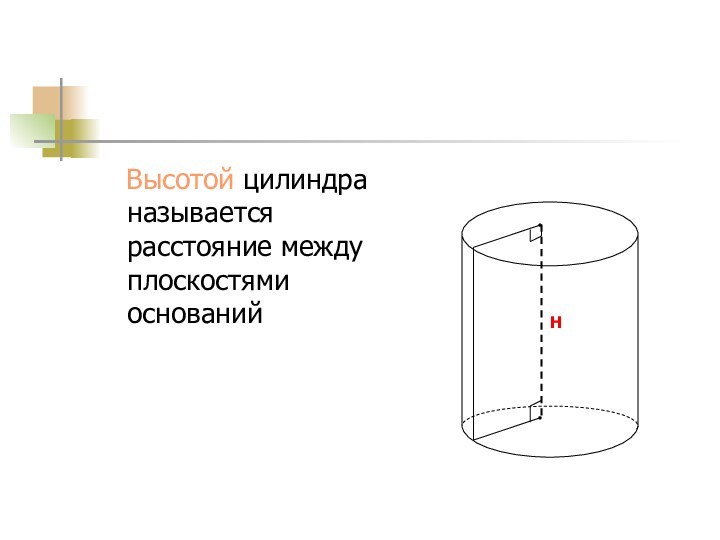
Слайд 6 Высотой цилиндра называется расстояние между плоскостями

оснований
Н

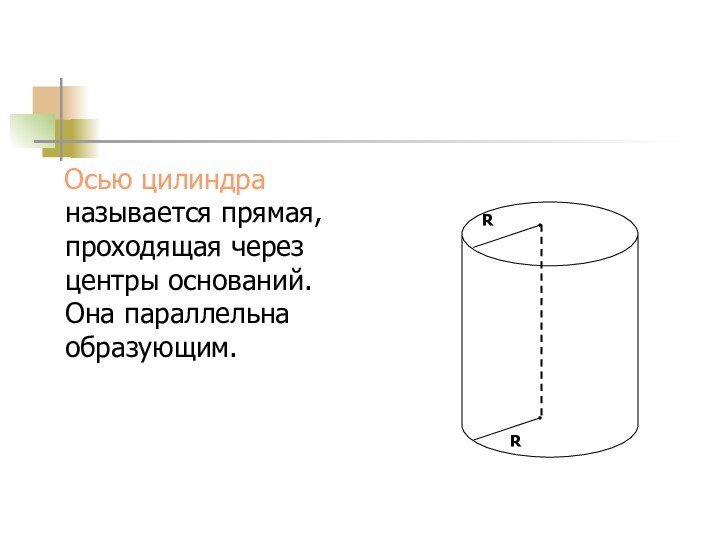
Слайд 7 Осью цилиндра называется прямая, проходящая через

центры оснований. Она параллельна образующим.
R
R

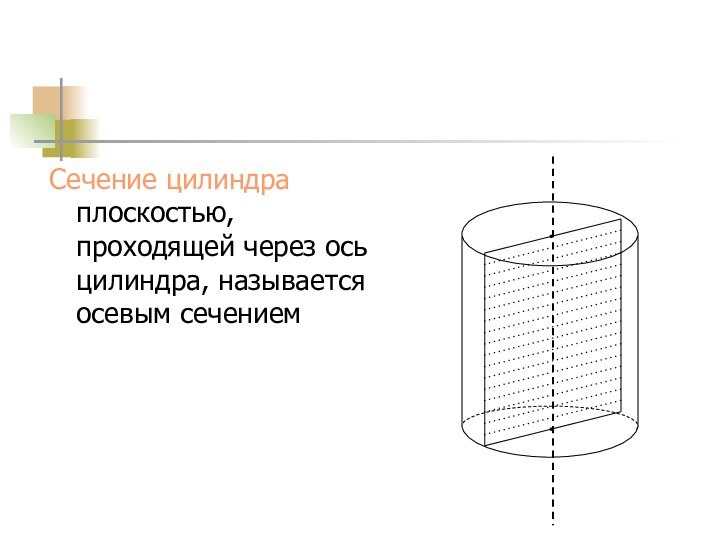
Слайд 8 Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется

осевым сечением

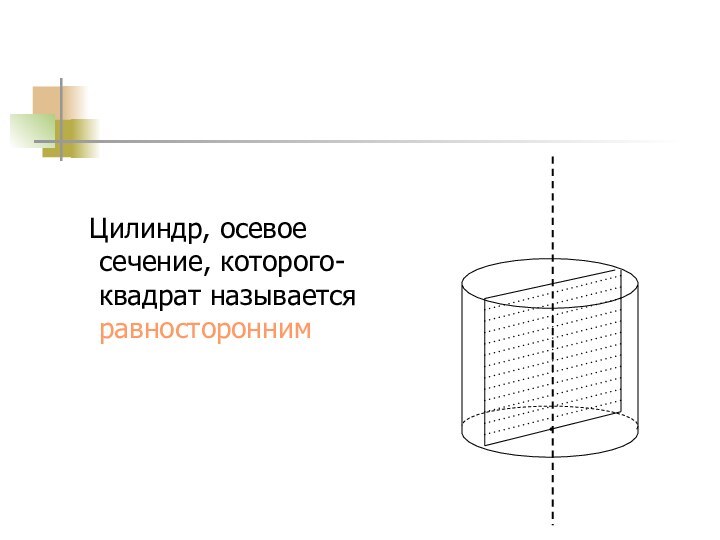
Слайд 9 Цилиндр, осевое сечение, которого-квадрат называется равносторонним

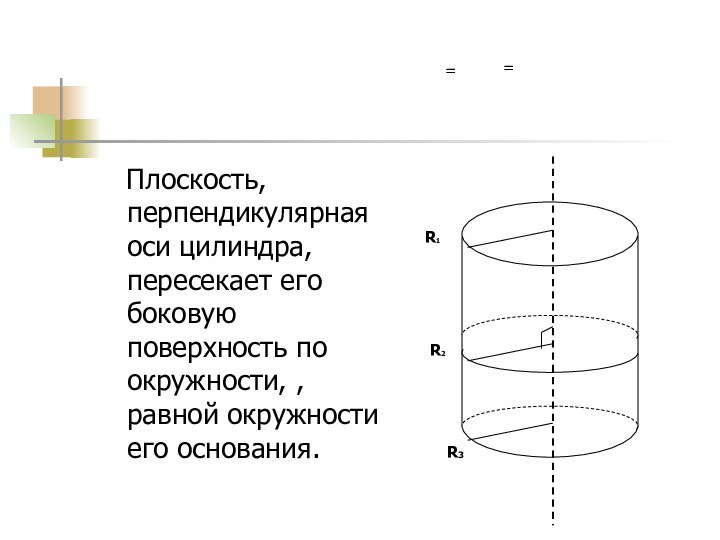
Слайд 10 Плоскость, перпендикулярная оси цилиндра, пересекает его

боковую поверхность по окружности, , равной окружности его основания.
R2
R3
R1
=
=

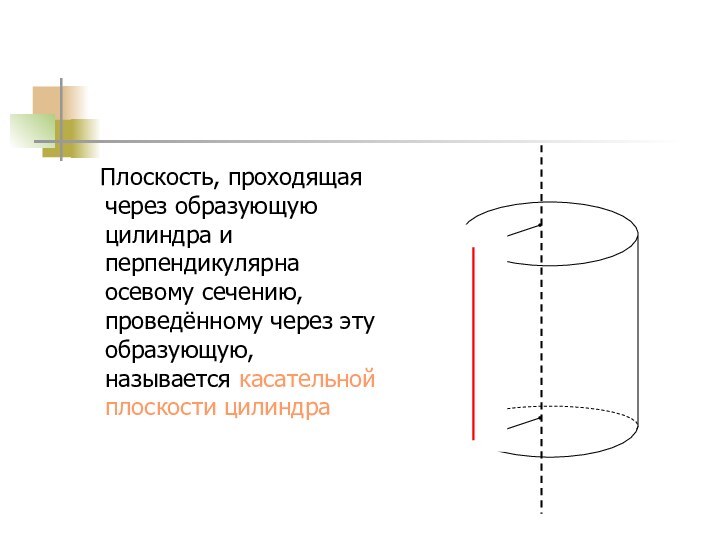
Слайд 11 Плоскость, проходящая через образующую цилиндра и

перпендикулярна осевому сечению, проведённому через эту образующую, называется касательной

плоскости цилиндра

Слайд 12 Задача № 1
Высота цилиндра 8 м,

радиус основания 5 м. Цилиндр пересечен плоскостью так, что

в сечении получился квадрат. Найдите расстояние от этого сечения до оси.

Слайд 13 Решение:

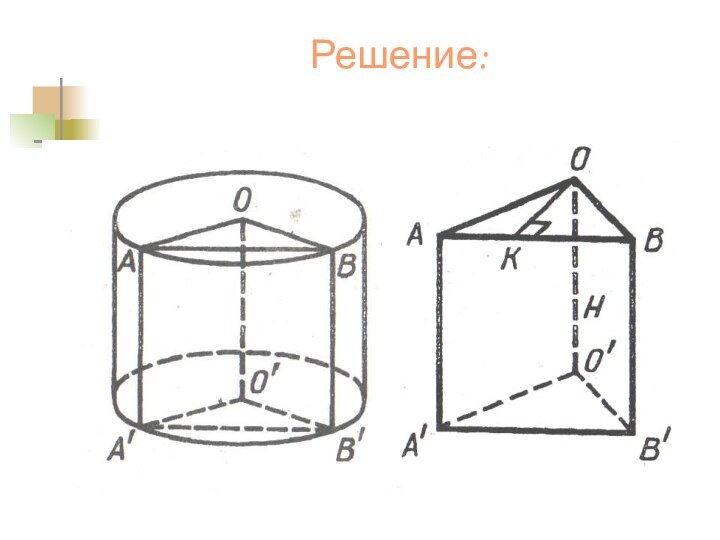
Слайд 14 1)Сечение АВВ'А' - квадрат
2) Фигура OAВO'A' В'- прямая

1)Сечение АВВ'А' - квадрат2) Фигура OAВO'A' В'- прямая треугольная призма, в

треугольная призма, в которой боковые ребра равны по 8

м ,стороны ОА=ОВ=R = 5 м, боковая грань АА'В' В - квадрат.
3) На рисунке призма АОВА'О'В' вынесена из цилиндра.
ОК AВ. Найдем, длину (h) перпендикуляра ОК.
4) По условию АВ = А'В' = М' = 8. В прямоугольном треугольнике АОК катет АК = 4. Тогда по теореме Пифагора
h = ОК = = = 3 м.

Слайд 15 Задача № 2
В цилиндр вписана правильная шестиугольная призма.

Задача № 2В цилиндр вписана правильная шестиугольная призма. Найдите угол между

Найдите угол между диагональю ее боковой грани и осью

цилиндра, если радиус основания равен высоте цилиндра.

Слайд 16 Решение:

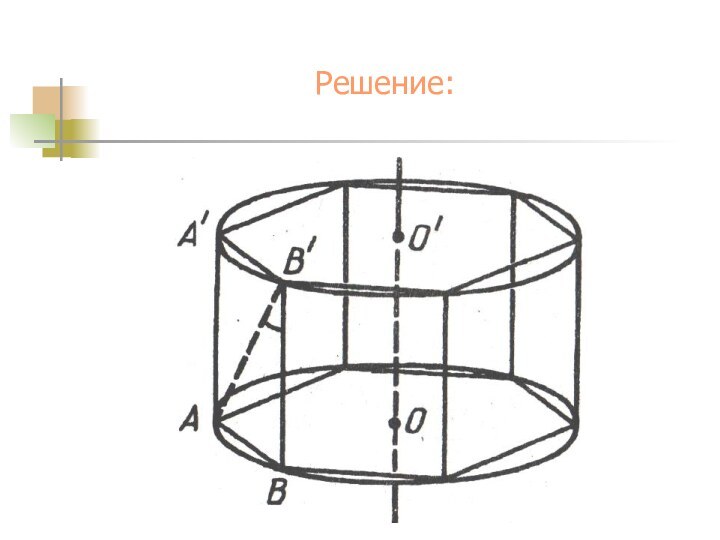
Слайд 17 1. Боковые грани призмы - квадраты, так как

1. Боковые грани призмы - квадраты, так как сторона правильного шестиугольника,

сторона правильного шестиугольника, вписанного в окружность, равна радиусу
2.

Ребра призмы параллельны оси цилиндра поэтому, угол между диагональю грани и осью цилиндра равен углу между диагональю и боковым ребром.
3. Так как грань призмы АА’B’B –квадрат, то этот угол равен 45о

Слайд 18 Задача № 3
Сережа насыпал в цилиндрическую

кастрюлю немного пшена и спросил соседку тетю Люду: «Сколько

нужно налить воды чтобы получилась вкусная каша? –«Это очень просто, - ответила соседка. - Наклони кастрюлю, постучи, чтобы крупа пересыпалась и закрыла ровно половину дна. Теперь заметь точку на стенке кастрюли у края, до которого поднялась крупа, зажми ее пальцем. До этого уровня надо налить воду!»- «Так ведь пшена можно насыпать побольше или поменьше, да и кастрюли бывают разные- широкие, узкие»,- усомнился Сережа. «Все равно, мой способ годиться в любом случае»,- гордо ответила соседка.

Докажите, что соседка права : отношение объемов воды и крупы по ее рецепту для любой цилиндрической кастрюли получается одинаковым. Найдите это отношение.

Слайд 19 Решение:

Слайд 20
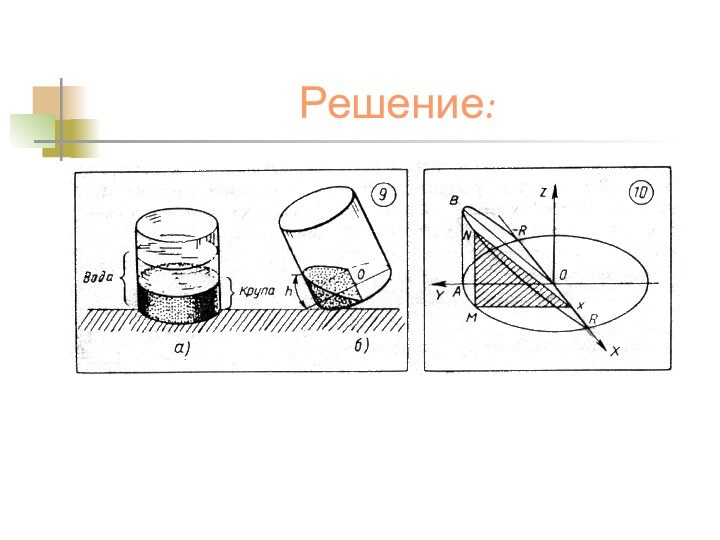
На рисунке слева изображена

стоящая кастрюля, а на рисунке справа- кастрюля, наклоненная так

,как советовала соседка. Поместим исследуемую модель в систему координат, чтобы основание цилиндра ( кастрюли ) лежало в плоскости XOY, а центр основания О стал началом координат. Через точку x на оси OX строим сечение тела( т.е. горки из крупы внутри кастрюли) плоскостью, перпендикулярной оси OX и параллельной оси OY