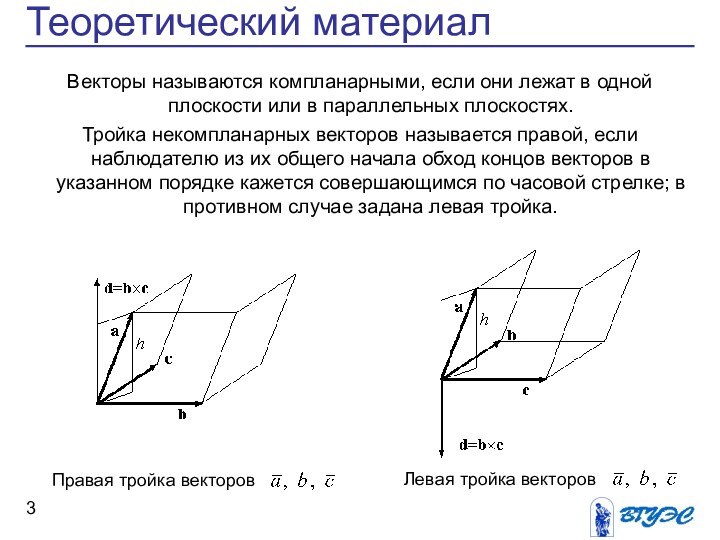
произведение двух векторов»
Задачи:
Ввести понятие векторного произведения двух векторов,
рассмотреть его свойства и геометрический смыслРассмотреть понятие смешанного произведения трех векторов, его свойства и геометрический смысл