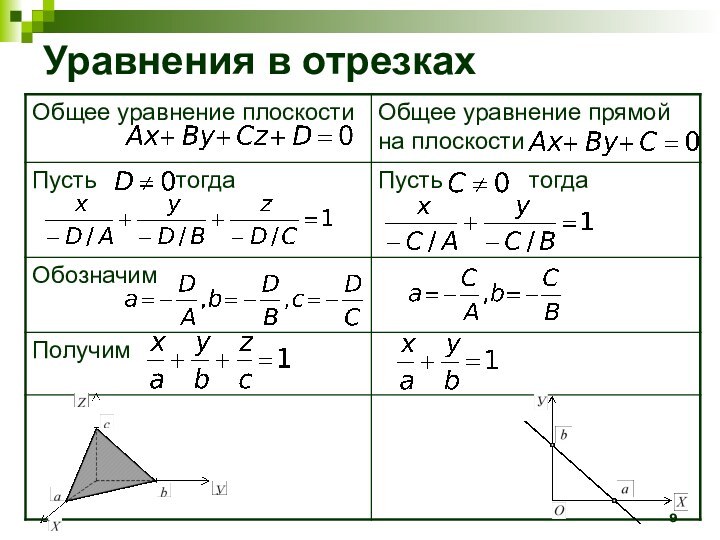
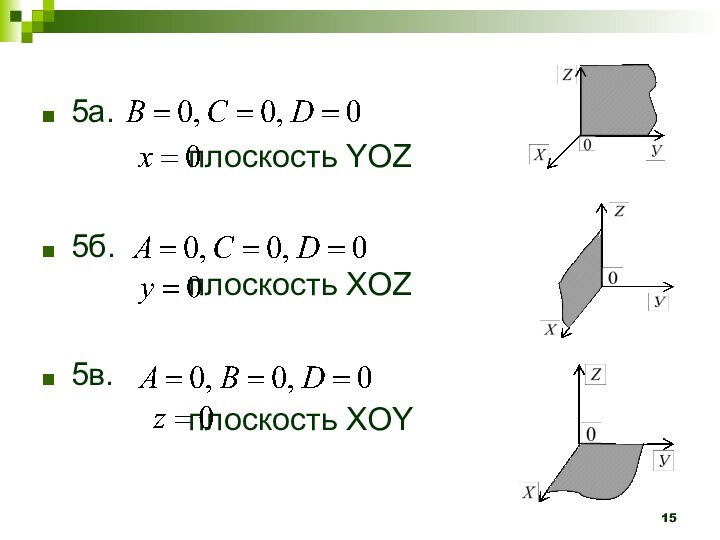
Опр. Геометрическое место точек
в пространстве (на плоскости) определяет
плоскость (прямую на плоскости) тогда и только тогда, когда декартовы координаты x, y, z текущей точки М удовлетворяют алгебраическому уравнению первого порядка