Презентация на тему МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ

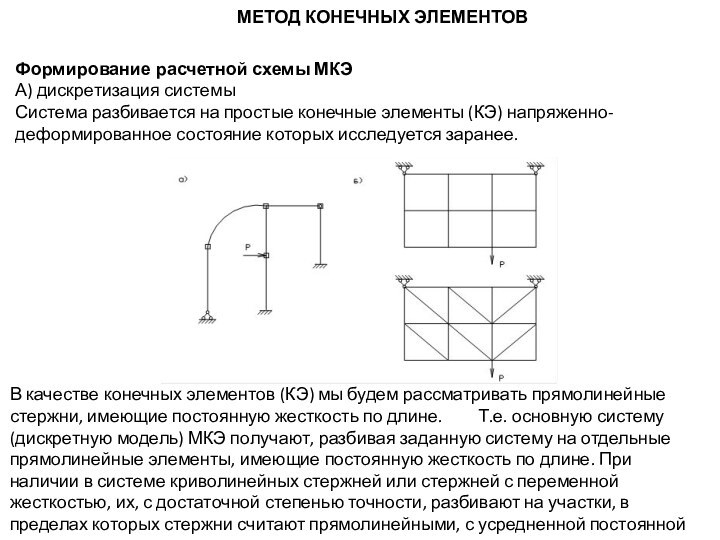
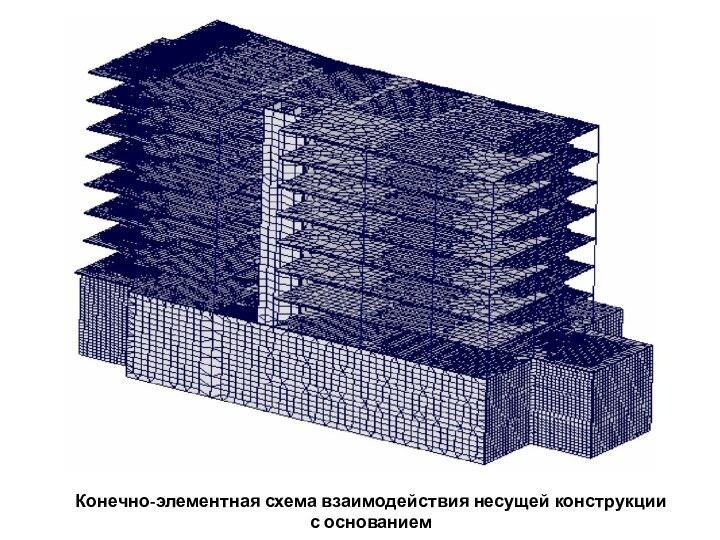
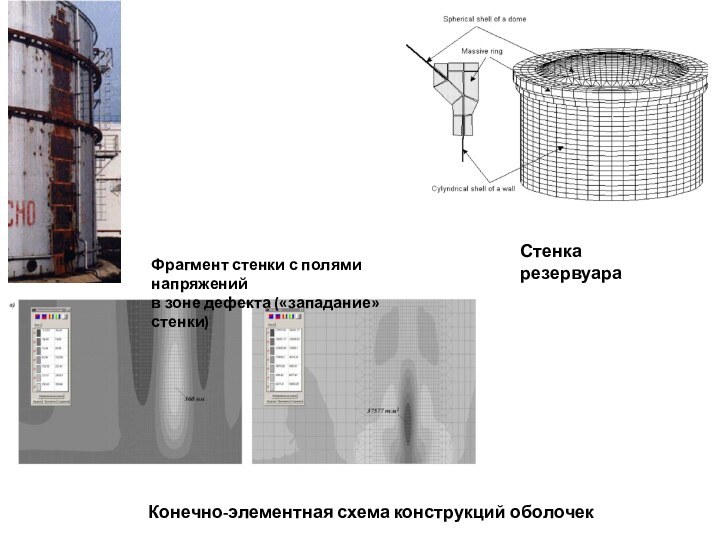
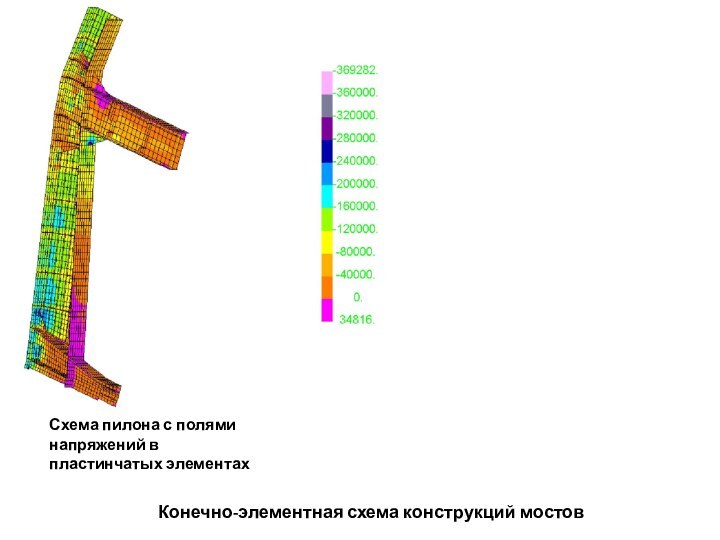
разбивается на простые конечные элементы (КЭ) напряженно-деформированное состояние которых

исследуется заранее.

В качестве конечных элементов (КЭ) мы будем рассматривать прямолинейные стержни, имеющие постоянную жесткость по длине. Т.е. основную систему (дискретную модель) МКЭ получают, разбивая заданную систему на отдельные прямолинейные элементы, имеющие постоянную жесткость по длине. При наличии в системе криволинейных стержней или стержней с переменной жесткостью, их, с достаточной степенью точности, разбивают на участки, в пределах которых стержни считают прямолинейными, с усредненной постоянной жесткостью.

г. Киеве. 55034 узлов, 63357
конечных элементов, 326 838 уравнений

число неизвестных МКЭ, определяется количеством наложенных в узлах дополнительных

связей.
В узлах, где отдельные элементы соединяются между собой жестко, имеется три неизвестных перемещения, в шарнирных узлах – два. Следовательно, количество неизвестных МКЭ можно определить:
n = 3nж.уз. + 2nш.уз .

Каждый элемент является частью заменяемой среды, т.е. сплошное тело лишь условно делится на отдельные элементы конечных размеров. Выделенный элемент имеет те же физические свойства и геометрические характеристики, что и рассматриваемая конструкция в месте расположения элемента.

б) узловые сопряжения
Между собой КЭ могут соединяться жестко или с помощью шарнира. Точки соединения элементов в МКЭ называют узловыми или узлами.

в) преобразование нагрузок
Кроме того, алгоритм МКЭ требует, чтобы все внешние нагрузки, действующие на сооружение, были приложены к узловым точкам ее дискретной модели. Поэтому, точки приложения сосредоточенных сил делают узловыми, а нагрузки распределенные по длине стержня, преобразуют к узловым.

сооружения в целом, которая связывается с общей системой осей

координат, характеризуется n параметрами перемещений Zi и узловых силовых воздействий Pi , составляющих векторы

В разрешающем уравнении МКЭ
[r]{Z}={P},
матрица [r], которая называется матрицей жесткости сооружения в целом, формируется из матриц жесткости отдельных элементов.

Каждый конечный элемент связан с местной системой осей координат и характеризуется своими параметрами узловых перемещений {V} и соответствующими узловыми усилиями {S}’.

колебаний

напряжений
в зоне дефекта («западание» стенки)

в
пластинчатых элементах