Слайд 2
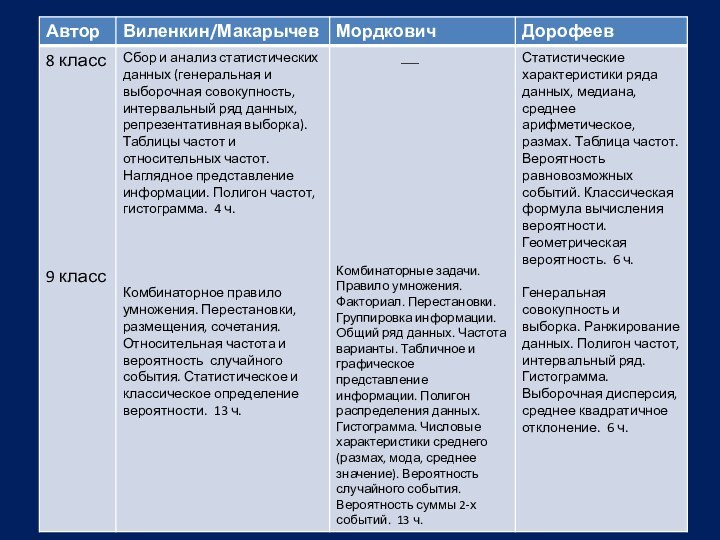
Вероятность и статистика (50 часов)
Описательная статистика. Представление данных
в виде таблиц, диаграмм, графиков. Случайная изменчивость. Статистические характеристики
набора данных: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах, дисперсия. Репрезентативные и нерепрезентативные выборки.
Случайные события и вероятность. Понятие о случайном опыте и случайном событии. Элементарные события. Частота случайного события. Статистический подход к понятию вероятности. Несовместимые события. Формула сложения вероятностей. Вероятности противоположных событий. Независимые события. Умножение вероятностей. Достоверные и невозможные события. Равновозможность событий. Классическое определение вероятности.
Комбинаторика. Решение комбинаторных задач перебором вариантов. Комбинаторное правило умножения. Перестановки и факториал.
Слайд 5
Перед нами нередко возникают проблемы, которые имеют не
одно, а несколько различных решений. Обычно одни из них
нас устраивают, а другие нет.
Рассмотрим первый пример.
Сколько двузначных чисел можно составить из цифр:
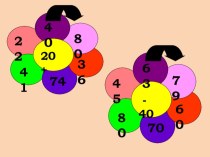
Слайд 6
Решение
Составим таблицу: слева от первого столбца
поместим первые цифры искомых чисел, а выше первой строки
– вторые цифры этих чисел.
11
14
17
41
44
47
71
74
77
9 чисел!
Слайд 7
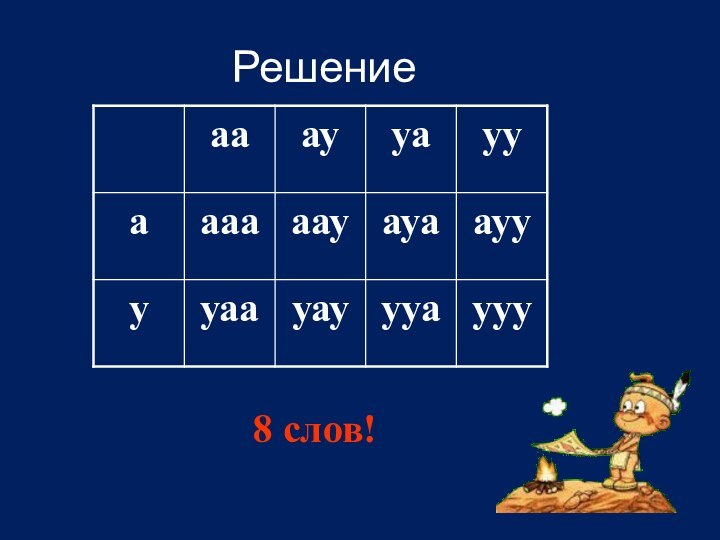
Второй пример: «В алфавите племени уауа имеются
только две буквы – «а» и «у».
Сколько различных
слов по три буквы в каждом слове можно составить, используя алфавит этого племени?»
Слайд 9
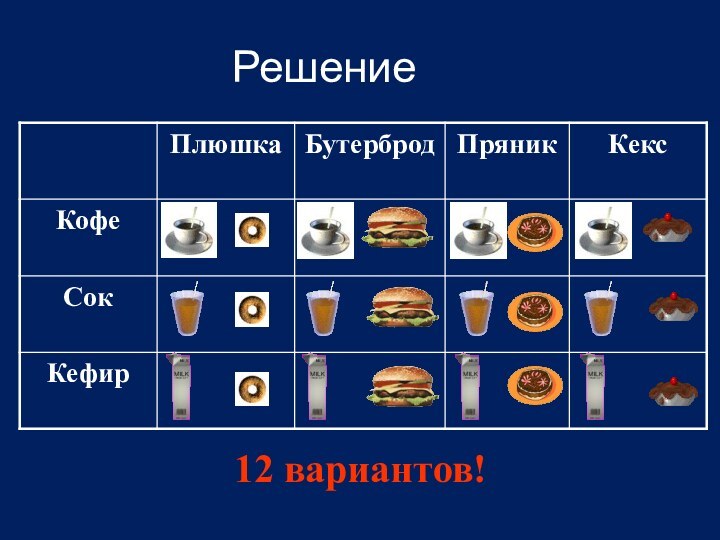
Третий пример: «На завтрак Вова может выбрать плюшку,
бутерброд, пряник или кекс, а запить их он может
кофе, соком или кефиром. Из скольких вариантов завтрака Вова может выбрать?»
Слайд 11
В данных примерах был осуществлен способ перебора возможных
вариантов (возможных комбинаций).
Поэтому данные задачи называют комбинаторными.
Решения данных задач
основывается на общем правиле умножения.
Слайд 12
«Правило умножения»
Для того чтобы найти число всех возможных
исходов независимого проведения двух испытаний А и В, следует
перемножить число всех исходов испытания А и число всех исходов испытания В.
Слайд 13
Правило умножения для трех, четырех и более испытаний
можно объяснить, не выходя за рамки плоскости, с помощью
геометрической модели, которую называют деревом возможных вариантов. Она, во-первых, наглядна, как всякая картинка, и, во-вторых, позволяет все учесть, ничего не пропустив.
Слайд 14
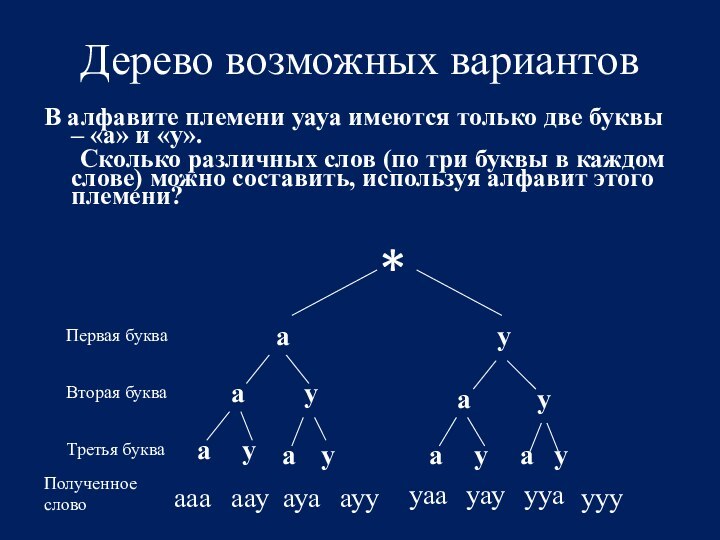
Дерево возможных вариантов
В алфавите племени уауа имеются только
две буквы – «а» и «у».
Сколько различных слов
(по три буквы в каждом слове) можно составить, используя алфавит этого племени?
*
Первая буква
Вторая буква
Третья буква
Полученное слово
Слайд 15
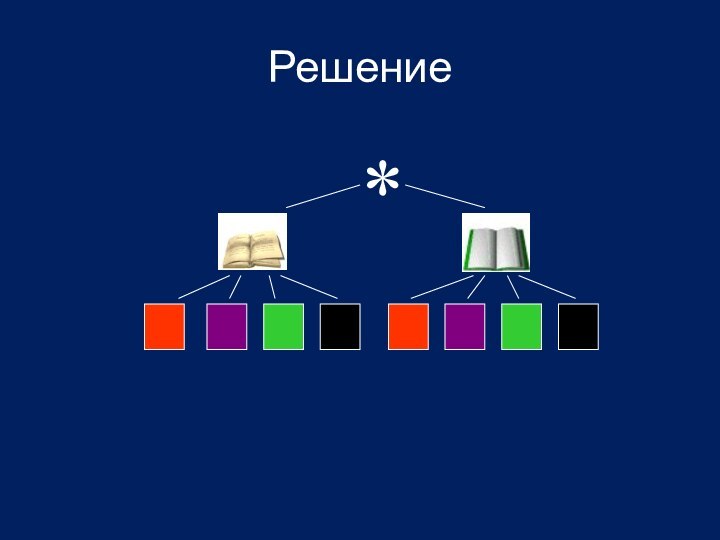
Задание 1
Имеются ручки четырех цветов: красные, синие, зеленые,
черные – и два вида записных книжек. Сколько различных
наборов из ручки и записной книжки можно составить из этих предметов?
Слайд 17
Задание 2
Шифр для сейфа составляют из букв и
цифр, причем на первом месте всегда ставится буква. Сколько
различных вариантов шифра можно составить, используя буквы А, В, С и цифры 3, 7, 9?
Слайд 18
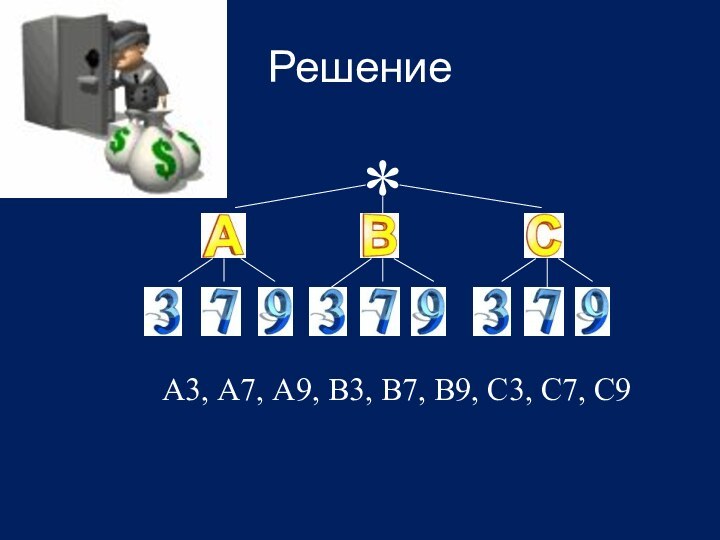
Решение
*
А3, А7, А9, В3, В7, В9, С3,
С7, С9
Слайд 19
Задание 3
Сколько можно составить различных букетов из трех
роз, если в продаже имеются белые и красные розы?
Слайд 20
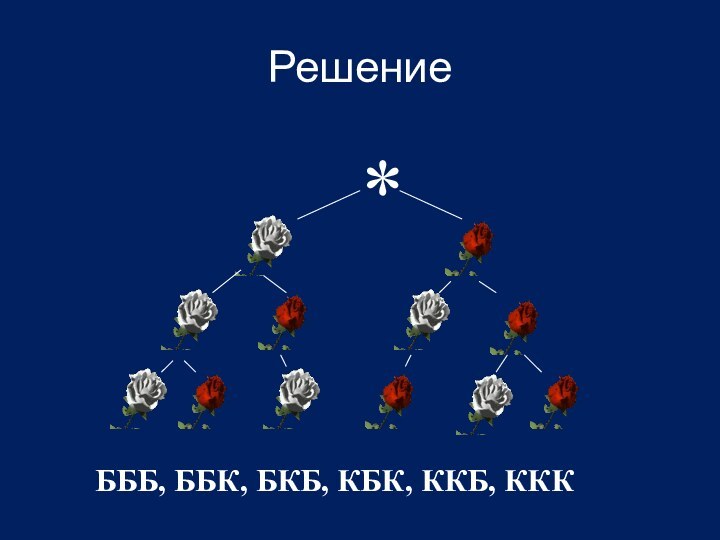
Решение
*
БББ, ББК, БКБ, КБК, ККБ, ККК
Слайд 21
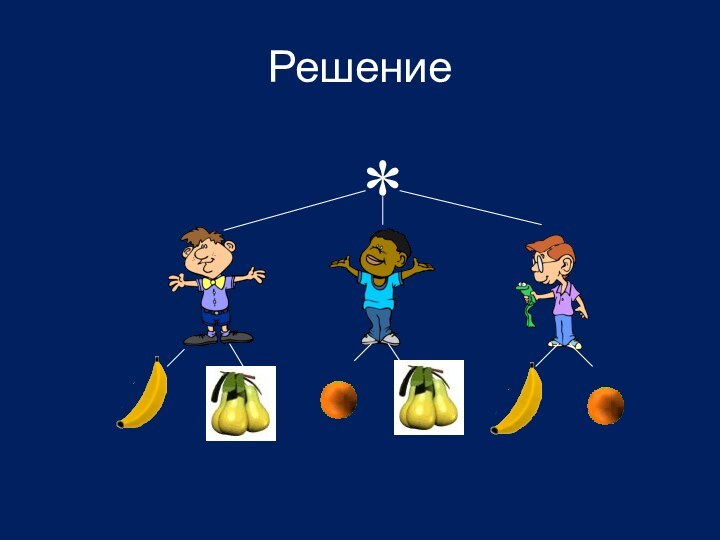
Задание 4
Сколькими способами три друга могут разделить
между собой два банана, две груши и два апельсина
так, чтобы каждый получил по два различных фрукта?
Слайд 24
Определения
События, которые при данных условиях обязательно происходят, называют
достоверными.
События, которые при данных условиях не могут произойти, называют
невозможными.
События, которые при данных условиях имеют равные шансы, называются равновероятными.
Слайд 25
Пример 1
В коробке лежат 5 конфет в синей
обертке и одна в белой. Не глядя в коробку,
наугад вынимают одну конфету. Можно ли сказать заранее, какого она будет цвета?
Слайд 26
Пример 2
В сумке лежат
4 красных и 4 желтых яблока. Из сумки наугад
вынимают яблоко. Какое из событий А, В, С, Д при этом может произойти?
А. Вынуто красное яблоко.
В. Вынуто желтое яблоко.
С. Вынуто зеленое яблоко.
Д. Вынуто яблоко.
Слайд 27
1 задание
Среди следующих событий укажите случайные,
достоверные и невозможные.
А. Попугай научится говорить.
В. Вы садитесь в
поезд и доезжаете до Северного полюса.
С. Наугад взятая с полки книга оказывается учебником математики.
Д. В полдень бьют Кремлевские часы.
Е. Вода в Тихом океане закипит.
Слайд 28
2 задание
Оцените возможность наступления событий, используя для этого
слова: «достоверное событие», «случайное событие», «невозможное событие», а также
«очень вероятное событие» и «маловероятное событие».
А. Завтра будет хорошая погода.
В. Вас пригласят в гости.
С. В январе в городе пойдет снег.
Д. В 12 часов ночи в городе идет дождь, а через 24 часа будет светить солнце.
Е. На день рождения вам подарят говорящего крокодила.
F. Вам подарят живого крокодила.
G. Вы получите «пятерку» за контрольную работу по математике.
Слайд 29
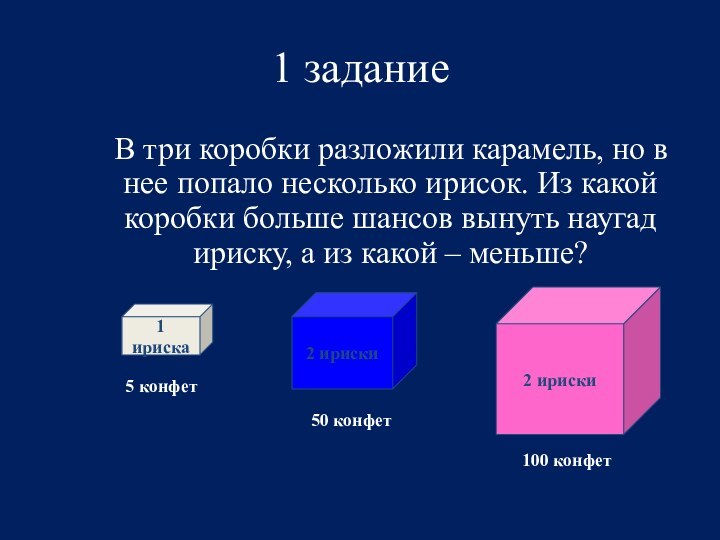
1 задание
В три коробки разложили карамель,
но в нее попало несколько ирисок. Из какой коробки
больше шансов вынуть наугад ириску, а из какой – меньше?
Слайд 30
Урезанное среднее.
Рассмотрим следующий пример. На олимпиаде по математике

предлагалось решить пять задач по 4 балла за каждую.
В протоколе указана сумма баллов каждого из восьми участников этой олимпиады:
12; 14; 14; 16; 17; 18; 19; 200.
Для ускорения подсчета имеется автоматизированная система обработки данных, которая находит среднее арифметическое любых введенных чисел. Какой средний балл набрали участники олимпиады?
У данного набора среднее равно 38,75. Однако такую сумму баллов никто из участников набрать не мог. К тому же семь чисел из данных восьми намного меньше его. Все значения этого набора, кроме крайнего правого, достаточно кучно попадают в интервал [12; 19], а 38,75 в него не попадает. Все это говорит о том, что полученное среднее арифметическое не только не передает особенностей данного набора чисел, но и вообще противоречит здравому смыслу. Значит, либо в условие, либо в решение вкралась ошибка! Посмотрим еще раз на данные числа. Теперь, получив явно бессмысленный результат, мы сможем более критически отнестись к условию: первые семь чисел вполне реальны, а вот последнее... Откуда оно взялось?! Видимо, оно случайно попало в этот список: возможно, в результате описки. Однако обнаружение ошибки в условии не избавляет нас от необходимости довести решение до конца. Можно, конечно, посоветовать комиссии снова переписать результаты учащихся и ввести числа из нового, «правильного» протокола. Но где гарантия, что в нем снова не будет опечатки?
Слайд 31
Когда все результаты более или менее кучно располагаются

на числовой оси, кроме, быть может, нескольких ненадежных значений,
анализировать результаты можно! Достаточно высокую точность полученных значений будет гарантировать применение других средних — в частности, урезанного среднего. Для его нахождения сначала упорядочивают набор по возрастанию, а затем отбрасывают слева и справа равное небольшое количество чисел. При этом «выбросы» (или ошибки наблюдений) в дальнейших вычислениях не участвуют. У полученного «урезанного» набора обычным образом находят среднее арифметическое. Оно и является урезанным средним исходного набора.
Вернемся к задаче. Если отбросить по одному числу с каждой стороны, то есть числа 12 и 200, то у оставшегося набора из шести чисел среднее равно 16,3
Это и есть урезанное среднее. Оно неплохо передает реальное среднее количество баллов, набранных юными математиками.
Некоторая аналогия с нахождением урезанного среднего просматривается в правилах судейства во многих видах спорта. Например, в соревнованиях по прыжкам с трамплина технику каждого прыжка оценивают 5 судей. Чтобы получить объективные оценки, две из них — высшую и низшую — отбрасывают, а для трех оставшихся находят сумму. Такой подход не дает возможности судьям повышать баллы своим соотечественникам, а спортсменам затрудняет нечестный путь к медалям.
Слайд 32
Задача.
4. На зимние каникулы в одной из школ города
Мурманска учительница дала детям задание: следить за погодой и
найти среднюю температуру. Ежедневно в течение десяти дней в 15 часов Наташа записывала показания термометра:
–13, –10, –15, 11, –9, –9, –11, –12, –10, –11.
А затем вычислила среднее арифметическое и получила –8,9.
а) Действительно ли в период наблюдений температура колебалась вблизи этого числа?
б) Почему большинство значений (9 из 10) меньше найденного среднего?
в) Как исправить ответ, если он неверный (заново повторить наблюдение, естественно, нельзя)?
а) Нет, в период наблюдений температура колебалась в промежутке [–15; –9], которому найденное среднее не принадлежит;
б) потому что имеется число 11, которое существенно отличается от всех остальных и поэтому меняет среднее в большую сторону;
в) найти урезанное среднее данного набора:
–9, –9, –10, –10, –11, –11, –12, –13, –15, 11. Оно приближенно равно -11,4.
Слайд 33
Задача.
1. Про отличника.
У отличника Коли были отметки по

математике «5», «5», «5», «5».
И вдруг в конце четверти
он получил «2». Он знает, что учитель математики выставляет четвертную отметку как среднее всех отметок, имеющихся у ученика, и не признает пересдач. Какое среднее было бы предпочтительнее для Коли, если он, естественно, надеется на пятерку в четверти?
Решение. 1. Попробуем начать с такого очень распространенного способа выставления четвертных отметок, как нахождение среднего арифметического:
Естественно, что любой учитель округлит этот результат в меньшую сторону и выставит итоговую отметку «4». Значит, это среднее Колю не устраивает.
Мы видим, что один неудачный ответ на балл снизил четвертную отметку. Ведь до этого среднее арифметическое равнялось 5.
2. Помочь Колиной мечте сбыться может другое среднее, и не одно! Например, если в качестве среднего учитель Коли возьмет медиану или урезанное среднее, то в четверти Коле обеспечена пятерка:
— медиана набора 2, 5, 5, 5, 5 равна 5;
— урезанное среднее набора 5, 5, 5, равно
Ответ: медиана или урезанное среднее.
Слайд 34
Наглядное представление статистической информации.
ДИАГРАММА (от греч. diagramma
-- изображение, рисунок, чертеж), графическое изображение, наглядно показывающее соотношение
каких-либо величин.
Универсальная энциклопедия Кирилла и Мефодия
Слайд 36
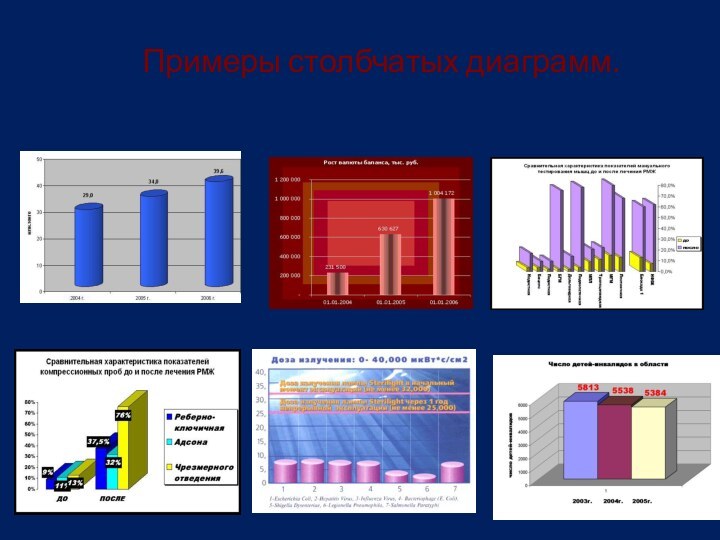
Изображения диаграмм могут быть самыми разнообразными.
Слайд 37
Какая диаграмма лучше?
Чаще всего(но не всегда) диаграммы взаимозаменяемы,
и одни и те же статистические данные можно представить
на различных диаграммах. Тем не менее, в каждом конкретном случае можно выбрать наиболее наглядный способ представления статистических данных:
график лучше всего подходит для того, чтобы показать динамику изменения величины во времени
столбчатая диаграмма удобна для сравнения абсолютных значений изучаемого признака
круговая диаграмма незаменима, когда нужно показать в какой пропорции целое делится на части(если количество частей невелико, иначе она теряет наглядность)
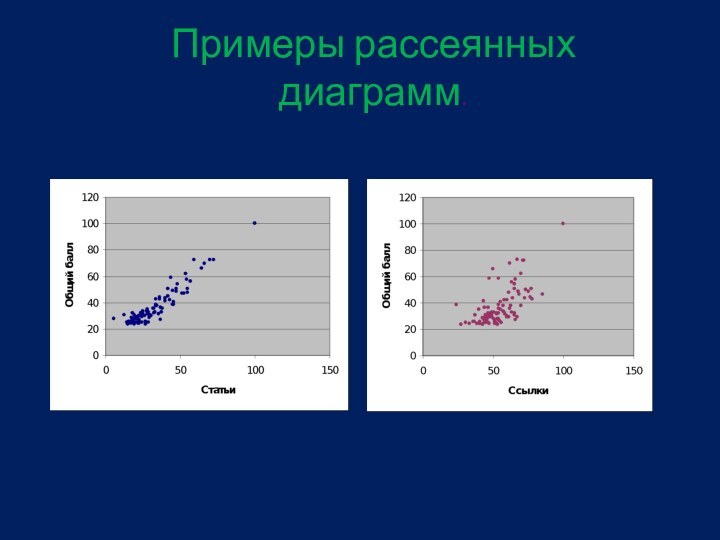
взаимосвязь двух величин лучше всего отражает рассеянная диаграмма.
Полигон частот используется для отображения данных частотных таблиц
Гистограмма отображает данные интервальной таблицы
Слайд 39
Диаграммы рассеивания.
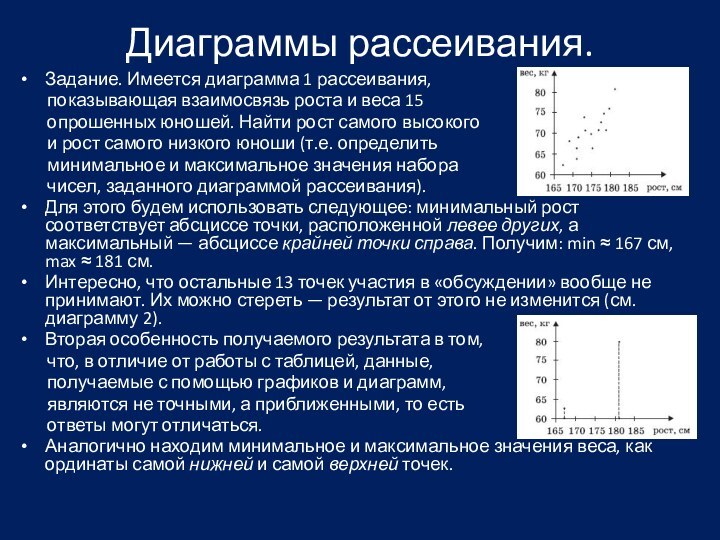
Задание. Имеется диаграмма 1 рассеивания,
показывающая взаимосвязь роста и веса 15
опрошенных юношей. Найти рост самого высокого
и рост самого низкого юноши (т.е. определить
минимальное и максимальное значения набора
чисел, заданного диаграммой рассеивания).
Для этого будем использовать следующее: минимальный рост соответствует абсциссе точки, расположенной левее других, а максимальный — абсциссе крайней точки справа. Получим: min ≈ 167 см, max ≈ 181 см.
Интересно, что остальные 13 точек участия в «обсуждении» вообще не принимают. Их можно стереть — результат от этого не изменится (см. диаграмму 2).
Вторая особенность получаемого результата в том,
что, в отличие от работы с таблицей, данные,
получаемые с помощью графиков и диаграмм,
являются не точными, а приближенными, то есть
ответы могут отличаться.
Аналогично находим минимальное и максимальное значения веса, как ординаты самой нижней и самой верхней точек.
Слайд 40
Задача 1.
У вас есть 9 разных книг из
серии «Занимательная математика». Сколькими способами можно:
а) расставить их
на полки;
б) подарить 3 из них победителям школьной олимпиады, занявшим первые три призовых места;
в) выбрать три из них для подарка своему племяннику;
г) распределить их поровну между тремя учениками.
Определите вид комбинации. Вычислите.
Слайд 41
Решение.
а) это перестановка
Р₉= 9! 9!=362980 способов расставить книги
на
полке.
б) это размещение
А³₉= 9!/6!=7·8·9=504 способа подарить три книги
победителям школьной олимпиады (с учетом порядка).
в) это сочетание
С³₉=9!/6!3!=7·8·9/2·3=84 способа выбрать три книги из девяти для подарка (порядок значения не имеет).
г) по правилу умножения
С³₉ · С³₆ · С³₃=84 · 20=1680 способов разделить поровну девять книг между тремя учениками.
Слайд 42
Задача 2.
Два стрелка сделали по одному выстрелу по
мишени. Вероятность попадания для первого стрелка 0,7, для второго
0,6. Какова вероятность, что:
а) оба промахнутся;
б) оба попадут;
в) хотя бы один попадет;
г) хотя бы один промахнется.
Слайд 43
Решение.
Рассмотрим события:
А= {первый стрелок попадет}
B= {второй стрелок попадет}
C=
{первый стрелок промахнется}
D= {второй стрелок промахнется}
События А и С,
В и D противоположные
Р(С)=1-Р(А)=1-0,7=0,3
Р(D)=1-Р(В)=1-0,6=0,4
а) Р(С D)=Р(С) · Р(D)=0,3 · 0,4=0,12
б) Р(А В)=Р(А) · Р(В)=0,7 · 0,6=0,42
в) Р(А υ В)=Р(А)+Р(В)-Р(А В)=0,7+0,6-0,42=0,88
г) Р(С υ D)=Р(С)+Р(D)-Р(С D)=0,3+0,4-0,12=0,58