Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Вероятность появления события

Содержание

2. Цель урока: ввести статистическое определение
3. Элементы комбинаторики. I. n!=
4. II. Перестановки – комбинации из
8. Элементы теории вероятности
10. Задачи: При ответе нужно
12. Письменный опрос 1 вариант1.
13. Элементы теории вероятности I. Эксперимент называют статическим,
15. II. Классическое определение вероятности события.
17. III. Статистическое определение вероятности событияИмеет место для испытаний с конечным числом неравновозможных исходов
20. Статистическое определение вероятности события обеспечивает нам
24. 1. Найдем n - общее число
25. Скачать презентацию
26. Похожие презентации

Цель урока: ввести статистическое определение вероятности события, понятие относительной частоты;систематизировать знания учащихся по статистическому и классическому определению вероятности события.

Главная
Математика
Вероятность появления события

Цель урока: ввести статистическое определение вероятности события,

Элементы комбинаторики. I. n!= 1х2х3х….х(n-2) (n-1) n произведение

II. Перестановки – комбинации из n элементов, которые отличаются друг

Задачи: При ответе нужно дать определение искомой величины, сказать

Письменный опрос 1 вариант1. Перестановки – формулаПример. 3

Элементы теории вероятности I. Эксперимент называют статическим, если он может быть повторен

II. Классическое определение вероятности события. имеет место для испытаний с

III. Статистическое определение вероятности событияИмеет место для испытаний с конечным числом неравновозможных исходов

Статистическое определение вероятности события обеспечивает нам принципиальную возможность оценки вероятности любого

1. Найдем n - общее число всех равновозможных несовместных исходов при

IV. Итог урока V. Домашнее задание. Тематический конспект «Элементы теории вероятности».

Слайды презентации

Слайд 2 Цель урока:
ввести статистическое определение вероятности события,

Цель урока: ввести статистическое определение вероятности события, понятие относительной

понятие относительной частоты;

систематизировать знания учащихся по статистическому

и классическому определению вероятности события.

Слайд 3 Элементы комбинаторики.
I.
n!= 1х2х3х….х(n-2) (n-1)

Элементы комбинаторики. I. n!= 1х2х3х….х(n-2) (n-1) n произведение подряд

n
произведение подряд идущих первых n натуральных чисел

0!=1; 1!=1; 2!=1х2=2; 3!=1х2х3=6; 4!=1х2х3х4=24
5! = 1х2х3х4х5 =120
6!= 720

Слайд 4 II. Перестановки – комбинации из n элементов, которые

отличаются друг от друга только порядком элементов.

Рn=n!
n –

число элементов, входящих в каждую перестановку,
(n- натуральное число)
(!!! Берутся все элементы, и изменяется только их местоположение)
Пример 1. Даны три лекарства А,В,С. Сколькими способами можно выписать назначение?
1способ решения; АВС, АСВ, ВСА, ВАС, САВ, СВА (6 способов назначения)
2 способ решения: Рn=n! Р3=3!=6
Пример 2. Сколько различных пятизначных чисел можно составить из цифр 5,6,7,8,9 при условии, что ни одна цифра в числе не повторяется? Решение. Р5=5!=120

Слайд 5

Слайд 6

Слайд 7

Слайд 8 Элементы теории вероятности

II. Классическое определение вероятности события.
(имеет место для испытаний с конечным числом равновозможных исходов испытания)

Слайд 9

Слайд 10 Задачи:

При ответе нужно дать определение

искомой величины, сказать формулу, по которой она находится.

Слайд 11

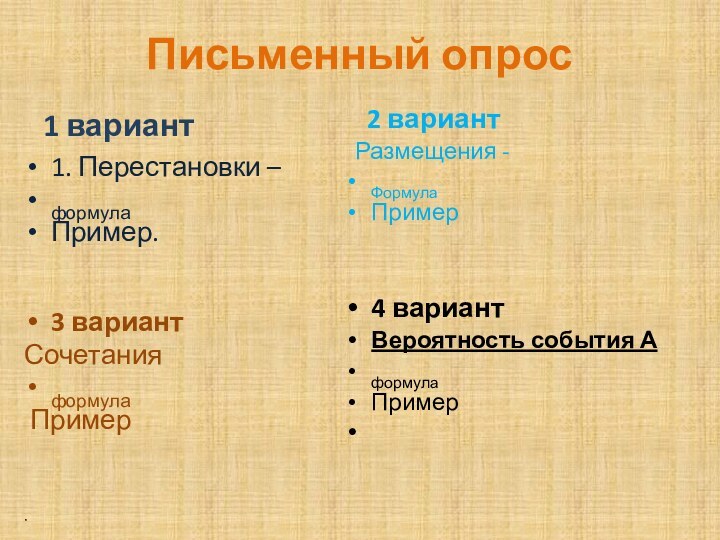
Слайд 12 Письменный опрос
1 вариант
1. Перестановки –

Письменный опрос 1 вариант1. Перестановки – формулаПример. 3 вариантСочетания формула Пример 2

формула
Пример.

3 вариант
Сочетания
формула
Пример

2 вариант

Размещения -
Формула
Пример

4 вариант
Вероятность

события А
формула
Пример

Слайд 13 Элементы теории вероятности
I. Эксперимент называют статическим, если

Элементы теории вероятности I. Эксперимент называют статическим, если он может быть

он может быть повторен в практически неизменных условиях неограниченное

число раз.

Слайд 14

Слайд 15 II. Классическое определение вероятности события.

имеет место для

испытаний
с конечным числом равновозможных исходов испытания

Слайд 16

Слайд 17 III. Статистическое определение вероятности события

Имеет место для испытаний

с конечным числом неравновозможных исходов

Слайд 18

Слайд 19

Слайд 20 Статистическое определение вероятности события обеспечивает нам

Статистическое определение вероятности события обеспечивает нам принципиальную возможность оценки вероятности

принципиальную возможность оценки вероятности любого события во всех случаях,

когда возможно проведение реальных экспериментов и изучение изменения относительной частоты по их результатам.
Случайные события со статистически устойчивой частотой широко распространены в физике, биологии, экономике и других областях знаний.

Слайд 21

Слайд 22

Слайд 23

Слайд 24 1. Найдем n - общее число всех

равновозможных несовместных исходов при вытягивании трех конфет. Их будет

столько, сколько можно составить различных размещений из 25 элементов по три: А253= = 25х24х23

2.Найдем m. Число случаев, благоприятствующих тому, что будут выбраны нужные три конфеты, столько, сколько можно составить перестановок из трех элементов
Р3= 3!= 1х2х3= 6.
3. Искомая вероятность равна
6\25х24х23 = 1\2300
Ответ: вероятность 1\2300