с зеркальной симметрией;
3. закрепить знания по видам симметрии
Цель урока:Введение в тему «Движения»
Задачи урока:
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть







Введение в тему «Движения»
Задачи урока:
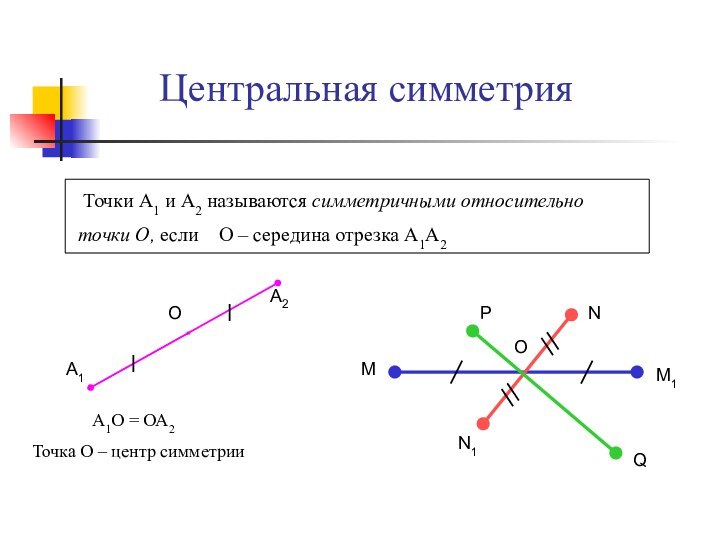
А1
А2
О
О
Р
Q
M
M1
N
N1
А1О = ОА2
Точка О – центр симметрии
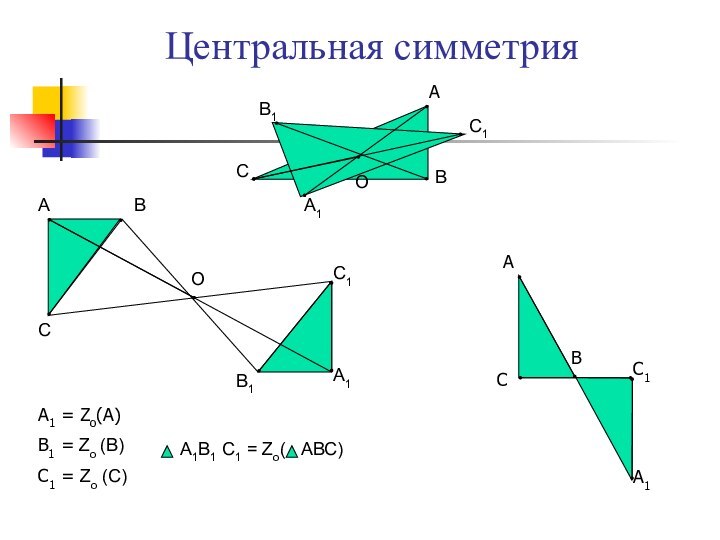
А
В
С
О
С1
А1
В1
А1В1 С1 = Zо( АВС)
О
А
С
В
А1
В1
С1
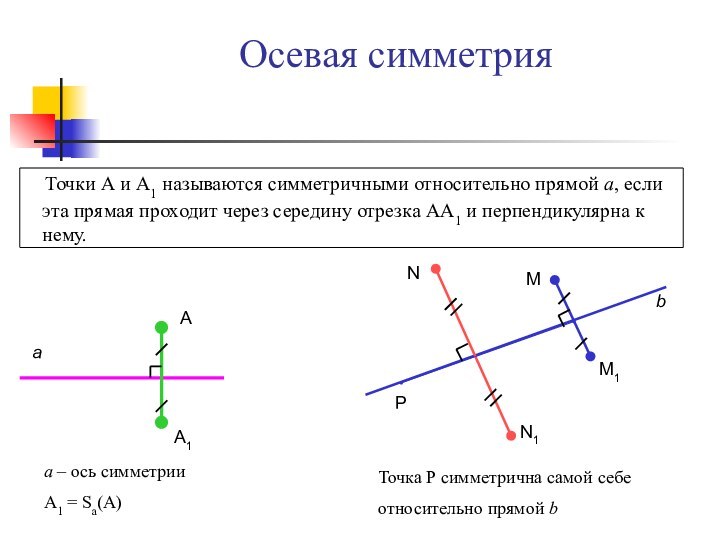
а
А
А1
а – ось симметрии
А1 = Sа(А)
Р
М
М1
b
N
N1
Точка Р симметрична самой себе
относительно прямой b
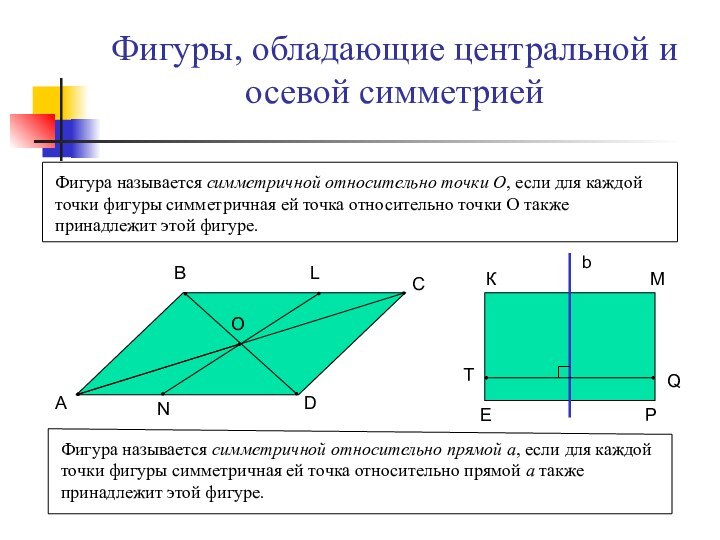
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
К
М
E
P
b
T
Q
А
В
С
D
k