- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Вневписанная окружность
Содержание
- 2. ЦельНаучиться решать геометрические задачи, которые приводят к появлению вневписанной окружности, и составить алгоритм их решения.
- 3. Задачи1. Ввести определение вневписанной окружности треугольника и
- 4. Понятие вневписанной окружностиОпределение: Вневписанной окружностью треугольника
- 5. Понятие вневписанной окружностиПусть на плоскости заданы три
- 6. Многие дают немедленный ответ: конечно одна, а
- 7. Аналогично, рассматривая другие пары внешних углов треугольника
- 8. Свойство вневписанной окружностиСвойство: Центр вневписанной окружности в
- 9. Свойство вневписанной окружностиДоказательство: Т. к. окружность
- 10. Вневписанная окружность в задачахПо итогам ОГЭ прошлого
- 11. Задача 1. Алгоритм решения1. Обозначить О –
- 12. Задача 2. Алгоритм решения1. Обозначить Q –
- 13. Задача 2. Алгоритм решения5. Рассмотреть подобные прямоугольные
- 14. Задача 2. Алгоритм решения8. Рассмотреть прямоугольный треугольник
- 15. Задача 3. Алгоритм решения1. Обозначить М –
- 16. ЗАДАЧА 1. Нахождение радиуса окружности вписанного в
- 17. ЗАДАЧА 1. Нахождение радиуса окружности вписанного в
- 18. ЗАДАЧА 2. Нахождение радиуса окруж - ности
- 19. ЗАДАЧА 2. Нахождение радиуса окруж - ности
- 20. ЗАДАЧА 2. Нахождение радиуса окруж - ности
- 21. ЗАДАЧА 3. Нахождение расстояния между прямыми.(Ященко И.В.,
- 22. ЗАДАЧА 3. Нахождение расстояния между прямыми.(Ященко И.В.,
- 23. ЗАКЛЮЧЕНИЕВ результате проделанной работы я выяснила, что
- 24. Скачать презентацию
- 25. Похожие презентации
ЦельНаучиться решать геометрические задачи, которые приводят к появлению вневписанной окружности, и составить алгоритм их решения.















![Вневписанная окружность ЗАДАЧА 1. Нахождение радиуса окружности вписанного в треугольник.(Демонстрационный вариант 2018г., КИМ[7])«Основание АС](/img/tmb/15/1435201/3b6ef75450a203bb79947838b56bd534-720x.jpg)
![Вневписанная окружность ЗАДАЧА 1. Нахождение радиуса окружности вписанного в треугольник.(Демонстрационный вариант 2018г., КИМ[7])∆AQO –](/img/tmb/15/1435201/eb07660ebd35555c8d1f5a204cfeee14-720x.jpg)
![Вневписанная окружность ЗАДАЧА 2. Нахождение радиуса окруж - ности описанной около треугольника.(Решу ОГЭ[9])«Две касающиеся](/img/tmb/15/1435201/cca2c3dc2fd86c0a672251b43c4ac51f-720x.jpg)
![Вневписанная окружность ЗАДАЧА 2. Нахождение радиуса окруж - ности описанной около треугольника.(Решу ОГЭ[9])Решение:Пусть Q](/img/tmb/15/1435201/a7a0815fc02dc6b6f60dee98bf6a4b9a-720x.jpg)
![Вневписанная окружность ЗАДАЧА 2. Нахождение радиуса окруж - ности описанной около треугольника.(Решу ОГЭ[9])Отрезки МС,](/img/tmb/15/1435201/a83baf0dfa7cffe1785ab62e8c8e069d-720x.jpg)



Слайд 2
Цель
Научиться решать геометрические задачи, которые приводят к появлению
вневписанной окружности, и составить алгоритм их решения.
Слайд 3
Задачи
1. Ввести определение вневписанной окружности треугольника и рассмотреть
ее свойство.
2.Проанализировать какие задачи в ОГЭ приводят к появлению
вневписанной окружности треугольника, и рассмотреть их решение.3.Составить алгоритм решения задач, которые приводят к появлению вневписанной окружности.
Слайд 4
Понятие вневписанной окружности
Определение:
Вневписанной окружностью треугольника называется окружность,
касающаяся одной из
его сторон и продолжений двух других.
Слайд 5
Понятие вневписанной окружности
Пусть на плоскости заданы три прямые,
которые попарно пересекаются в точках A, B и C
(рис.1). Вопрос: сколько существует точек, равноудаленных от этих прямых?Слайд 6 Многие дают немедленный ответ: конечно одна, а именно,
центр окружности, вписанной в треугольник ABC(рис.1), но этот ответ
неверен. Действительно, рассмотрим, например, биссектрисы внешних углов B и C треугольника ABC (рис.3). Так как сумма углов, образованных ими со стороной BC, меньше, чем 180°, то эти биссектрисы пересекутся в некоторой точке ОА. Тогда точка ОА равноудалена от прямых AB, AC и BC.Слайд 7 Аналогично, рассматривая другие пары внешних углов треугольника ABC,
получим еще две точки, обладающие требуемым свойством. Таким образом,
помимо центра окружности О, вписанной в треугольник АВС, существуют, по крайней мере, еще три точки ОA, ОB, ОC равноудаленные от заданных прямых. Каждая из этих точек является центром окружности, касающейся стороны треугольника и продолжений двух других сторон.Определение: Вневписанной окружностью треугольника называется окружность, касающаяся одной из его сторон и продолжений двух других[2,11].
Слайд 8
Свойство вневписанной окружности
Свойство: Центр вневписанной окружности в треугольник
есть точка пересечения биссектрисы внутреннего угла треугольника, противолежащего той
стороне треугольника, которой окружность касается, и биссектрис двух внешних углов треугольника.
Слайд 9
Свойство вневписанной окружности
Доказательство:
Т. к. окружность касается сторон
угла САК, то центр окружности О равноудален от сторон
этого угла, следовательно, он лежит на биссектрисе угла САК. Аналогично, точка О лежит на биссектрисе угла АСN. Т. к. окружность касается прямых ВА и ВС, то она вписана в угол АВС, а значит, её центр лежит на биссектрисе угла АВС. Ч.т. д.
Слайд 10
Вневписанная окружность в задачах
По итогам ОГЭ прошлого года
многие девятиклассники даже не приступали к решению задач №26[8].
Проанализировав
эти задания[4,6-10,12], я заметила, что в №26 встречаются три вида задач про вневписанную окружность и что условия следующих задач не содержат термина «вневписанная окружность». Она появляется в решении как вспомогательная фигура.
Слайд 11
Задача 1. Алгоритм решения
1. Обозначить О – центр
вневписанной окружности, Q – центр окружности, вписанной в треугольник
АВС, М – точку касания окружностей.2. Вычислить АМ=СМ= СА:2 = а:2.
3. Рассмотреть лучи AQ и АО как биссектрисы смежных углов и сделать вывод что угол ОAQ прямой.
4. Рассмотреть прямоугольный треугольник AQО и используя свойство пропорциональных отрезков записать: АМ2= QМ·МO.
5. Вычислить QМ= AМ2МO= (а:2)2?
6. Записать ответ.
Слайд 12
Задача 2. Алгоритм решения
1. Обозначить Q – центр
вневписанной окружности, О – центр окружности, вписанной в треугольник
АВС, QМ и ОN- радиусы, проведенные в точки касания окружностей с прямой АС, S- центр окружности описанной около треугольника АВС, r – радиус окружности, описанной около треугольника АВС.2. Рассмотреть лучи ВО и ВQ как биссектрисы смежных углов и сделать вывод что угол ОAQ прямой.
3. Рассмотреть прямоугольный треугольник ВОQ и используя свойство пропорциональных отрезков вычислить ВК по формуле ВК =√ОК ·?? = √а·b.
4. Обозначить АN через х.
Слайд 13
Задача 2. Алгоритм решения
5. Рассмотреть подобные прямоугольные треугольники
ANO и АМQ и найти коэффициент подобия как отношение
радиуса вневписанной окружности к вписанной: k=b/a. Обозначить через полученное значение k: АМ = k х, MN = k х - х=(k-1)х.6. Рассмотреть равные отрезки МС, СК и СN, как касательные, проведенных из одной точки, и вычислить СN=СК=СМ=√а·?, МN=2СК=2√а·?, затем AN=x=2√а·b :((k-1)х), АB = АС= АN + NС=2√а·b :((k-1)х)+√а·b.
7. Рассмотреть прямоугольный треугольник АВК и найти АК: АК=√AВ²−ВК².
Слайд 14
Задача 2. Алгоритм решения
8. Рассмотреть прямоугольный треугольник SВК,
в котором по теореме Пифагора r2 = (АК -
r)2 +ВК2 , выразить и вычислить ?= AВ² 2АК.9. Записать ответ.
Слайд 15
Задача 3. Алгоритм решения
1. Обозначить М – центр
вневписанной окружности, О – центр вписанной окружности и вычислить
ОМ= а + ?.2. Провести перпендикуляр ОР из центра вписанной окружности на радиус МС вневписанной окружности. Вычислить МР = МС - РС =МС – ОА= ?- а.
3. Рассмотреть прямоугольный треугольник ОРМ и найти ОР =√ОМ²−МР².
4. Опустить перпендикуляр BQ из точки В на прямую СD. Рассмотреть прямоугольные треугольники: BQD и ОРМ (подобны по двум углам), записать BQ/BD=OP/ОМ. Откуда вычислить ВQ= OP ·BDОМ.
5. Записать ответ.
Слайд 16
ЗАДАЧА 1. Нахождение радиуса окружности вписанного в треугольник.
(Демонстрационный
вариант 2018г., КИМ[7])
«Основание АС равнобедренного треугольника равно 12. Окружность
радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания АС. Найдите радиус окружности вписанной в треугольник АВС».Решение:
Сделаем чертеж к данной задачи. Так как окружность касается стороны треугольника и продолжения двух других сторон, то – это вневписанная окружность.
Пусть О – центр вневписанной окружности, Q – центр окружности, вписанной в треугольник АВС.
Так как центр вписанной окружности и вневписанной окружности лежит в точке пересечения биссектрис, то AQ -биссектриса угла ВАС, а AO – биссектриса смежного с ним угла.
Слайд 17
ЗАДАЧА 1. Нахождение радиуса окружности вписанного в треугольник.
(Демонстрационный
вариант 2018г., КИМ[7])
∆AQO – прямоугольный треугольник, так как биссектрисы
смежных углов образуют прямой угол.АМ – высота, проведенная к гипотенузе, АМ = ½ АС = 6.
AМ²= QМ·МO. Следовательно, QМ= AМ² МO=6² 8=36 8=4,5
QМ – радиус вписанной в ∆АВС окружности, следовательно r = 4,5.
Ответ: 4,5.
Слайд 18 ЗАДАЧА 2. Нахождение радиуса окруж - ности описанной около
треугольника.
(Решу ОГЭ[9])
«Две касающиеся внешним образом в точке К окружности,
радиусы которых равны 36 и 45, вписаны в угол с вершиной А. Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С. Найдите радиус окружности, описанной около треугольника АВС.»Слайд 19 ЗАДАЧА 2. Нахождение радиуса окруж - ности описанной около
треугольника.
(Решу ОГЭ[9])
Решение:
Пусть Q – центр вневписанной окружности, О –
центр вписанной окружности в треугольник ABC, QМ и ОN- радиусы, проведенные в точки касания окружностей с прямой АС, S- центр окружности описанной около треугольника АВС, r – радиус окружности, описанной около треугольника АВС.ВО -биссектриса угла АВК, а ВQ – биссектриса смежного с ним угла. Значит ∆OBQ – прямоугольный. Следовательно, находим ВК =√ОК ·??=√36·45=18 √5.
Пусть АN = х. Прямоугольные треугольники ANO и АМQ подобны с коэффициентом 45/36 = 1,25, значит, АМ = 1,25х, MN = 0,25х.
Слайд 20 ЗАДАЧА 2. Нахождение радиуса окруж - ности описанной около
треугольника.
(Решу ОГЭ[9])
Отрезки МС, СК и СN равны как отрезки
касательных, проведенных из одной точки, значит, ВК = СК =18√5, 0,25х = МN=2СК= 36√5, откуда AN=x=144√5, АС =АB =1,125х= 162√5.В прямоугольном треугольнике АВК находим катет АК:
АК =√AВ²−ВК² =360.
В прямоугольном треугольнике SВК по теореме Пифагора имеем r2 = (АК - r)2 +ВК2,
?= AВ² 2АК=1622·5 2·360=182,25
Ответ: 182,25.
Слайд 21
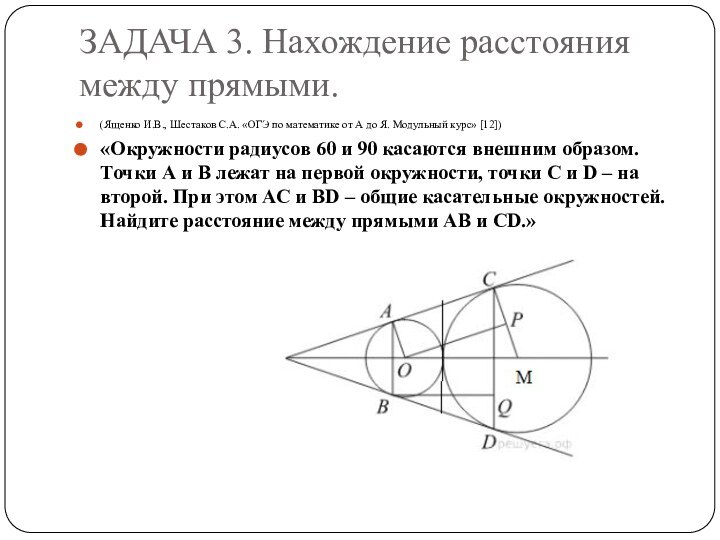
ЗАДАЧА 3. Нахождение расстояния между прямыми.
(Ященко И.В., Шестаков
С.А. «ОГЭ по математике от А до Я. Модульный
курс» [12])«Окружности радиусов 60 и 90 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D – на второй. При этом АС и ВD – общие касательные окружностей. Найдите расстояние между прямыми АВ и СD.»
Слайд 22
ЗАДАЧА 3. Нахождение расстояния между прямыми.
(Ященко И.В., Шестаков
С.А. «ОГЭ по математике от А до Я. Модульный
курс» [12])Решение:
Линия центров вписанной и вневписанной окружностей проходит через точку касания, поэтому расстояние между центрами окружностей равно сумме их радиусов, т.е. ОМ=150. Опустим перпендикуляр ОР из центра меньшей окружности на радиус МС второй окружности. Тогда МР = МС-РС =МС – ОА=90-60=30
Из прямоугольного треугольника ОРМ находим, что ОР =√ОМ²−РМ² = 60√6
Опустим перпендикуляр BQ из точки В на прямую СD. Прямоугольный треугольник BQD подобен прямоугольному треугольнику ОРМ по двум углам, поэтому BQBD=OPОМ. Следовательно, ВQ= OP ·BDОМ=60√6·60√6150=144.
Ответ: 144.
Слайд 23
ЗАКЛЮЧЕНИЕ
В результате проделанной работы я выяснила, что собой
представляют вневписанные окружности треугольника, каким свойством они обладают[2-4]. Оказалось,
что вневписанные окружности треугольника используются в школьной программе мало, но зато их можно встретить на олимпиадах, ОГЭ[2-12].Проанализировав задания[4,6-10,12], которые приводят к появлению вневписанной окружности, я заметила, что встречаются три вида задач про вневписанную окружность и что условия следующих задач не содержат термина «вневписанная окружность». Она появляется в решении как вспомогательная фигура. Также во всех задачах совпадают обозначения, отличаются только числовые значения. Используем эти обозначения при составлении алгоритма решения задач, которые приводят к появлению вневписанной окружности. Данные алгоритмы помогут другим учащимся полноценно подготовиться к ОГЭ по данной теме. Используя которые учащимся будет очень легко решить задачи, подставив свои значения.





























