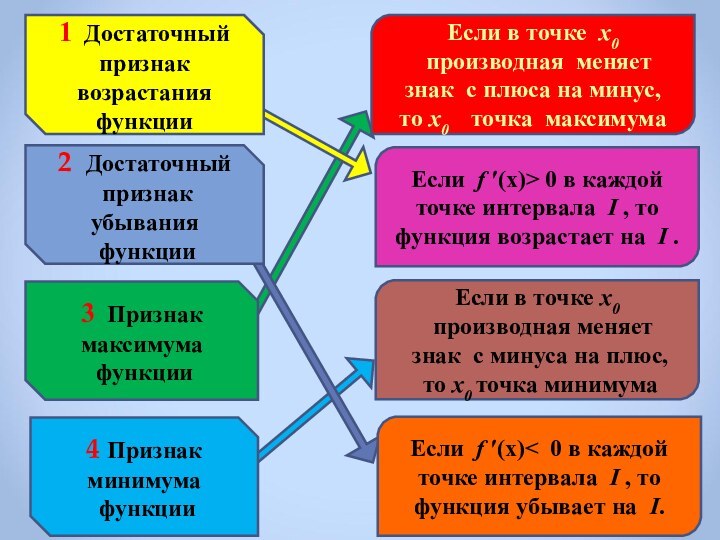
Признак
максимума
функции
4 Признак
минимума
функции
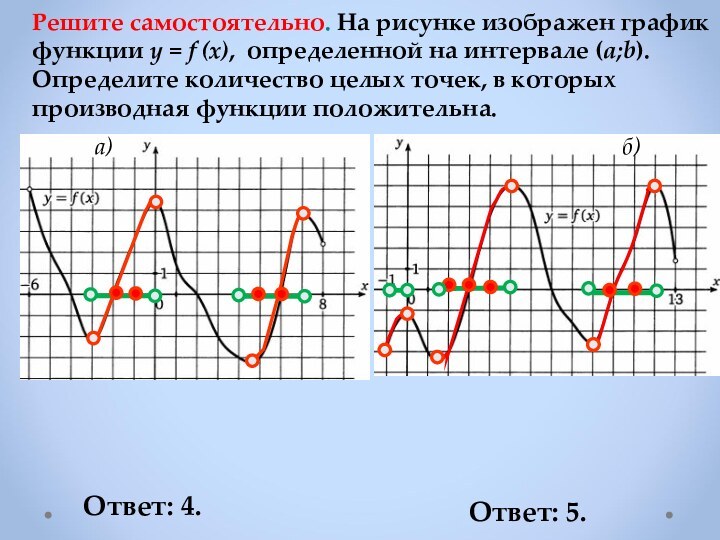
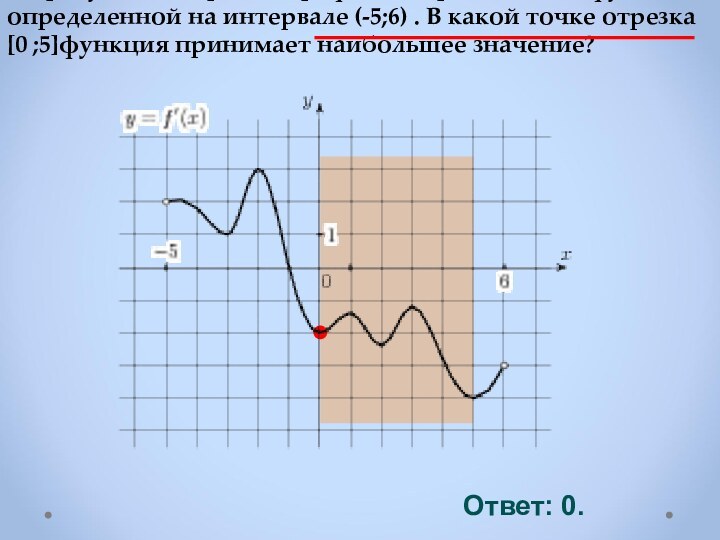
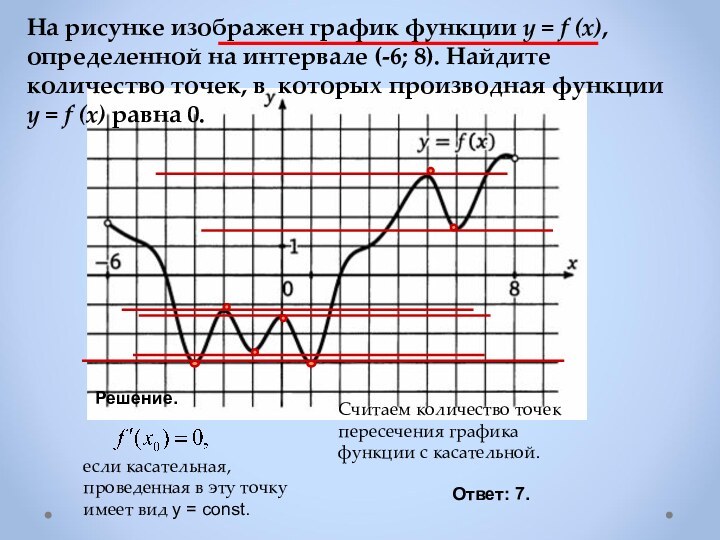
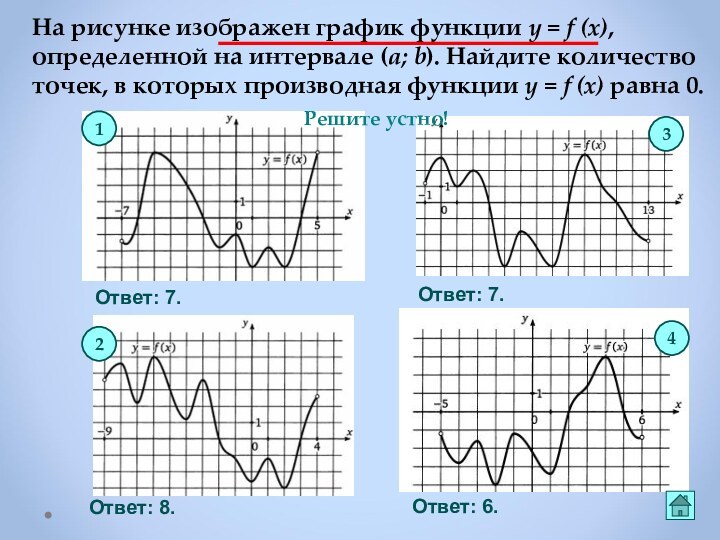
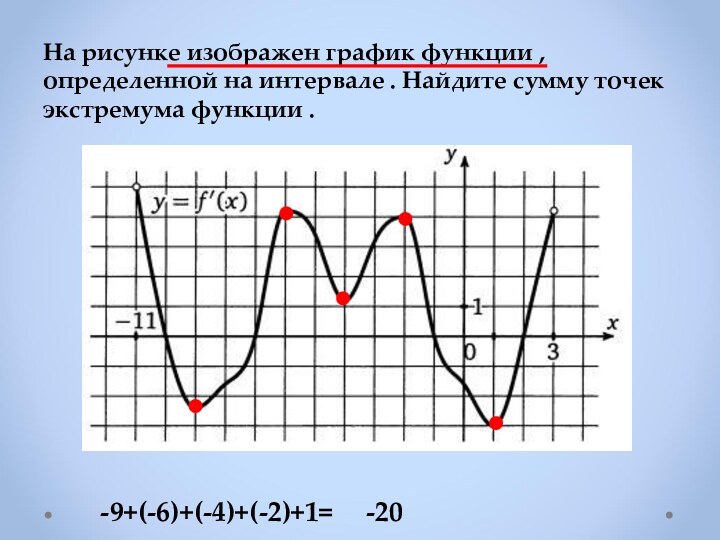
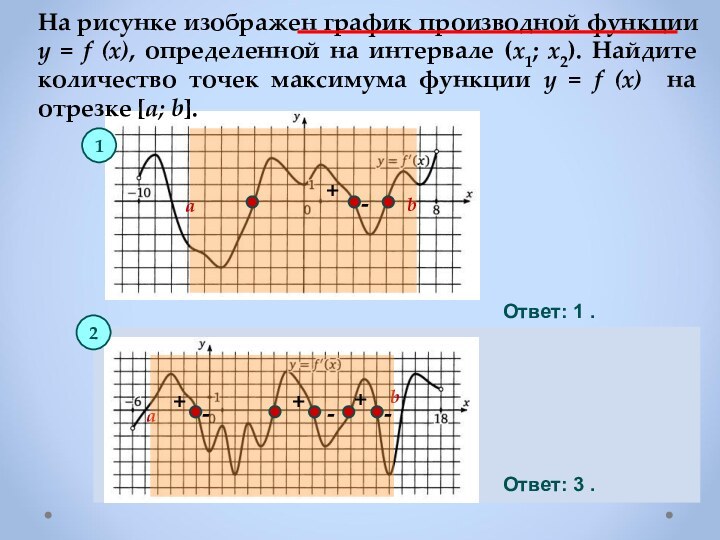
Если в точке х0
производная меняет знак с плюса на минус,
то х0 точка максимума
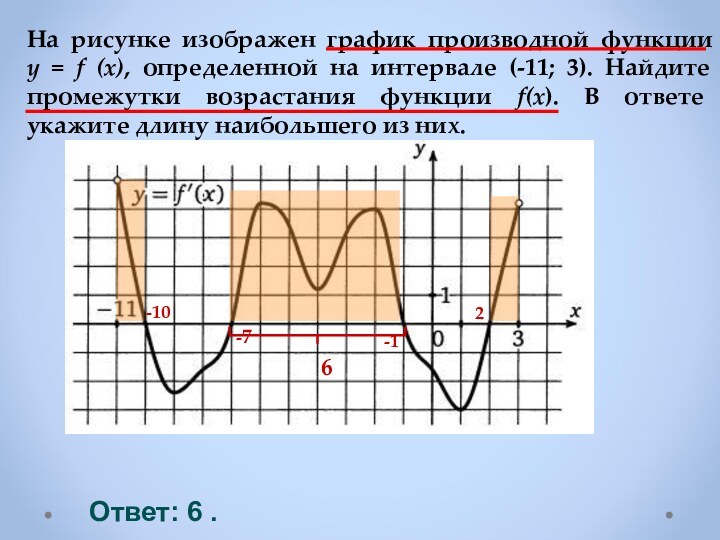
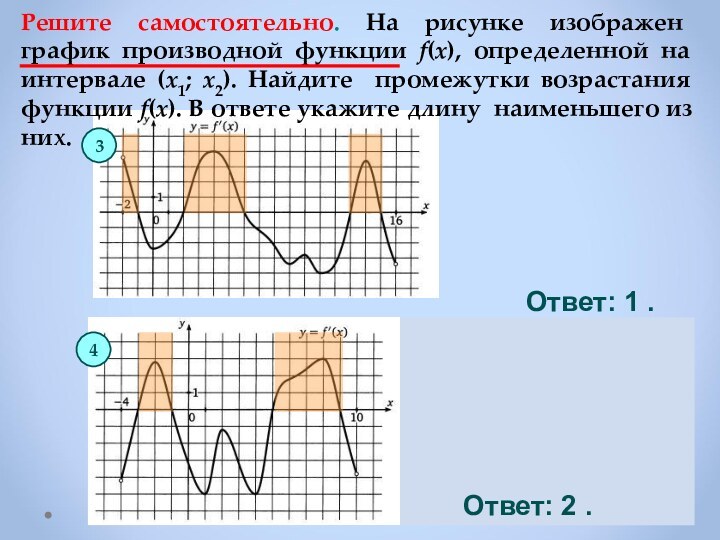
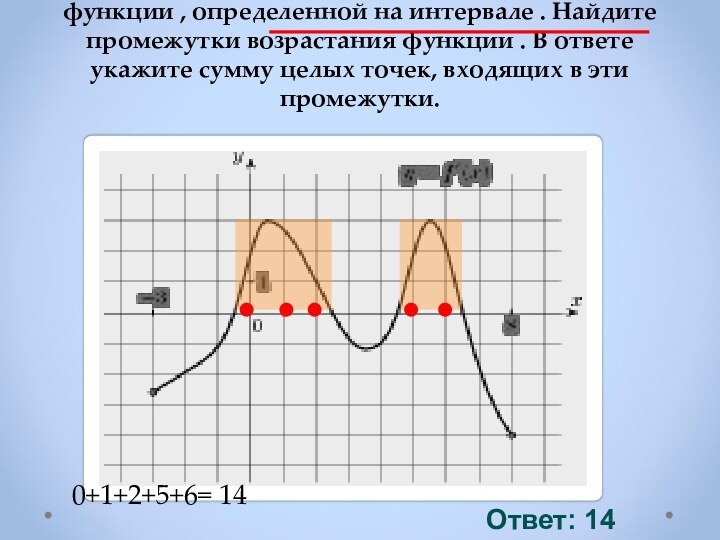
Если f ′(х)> 0 в каждой точке интервала I , то
функция возрастает на I .
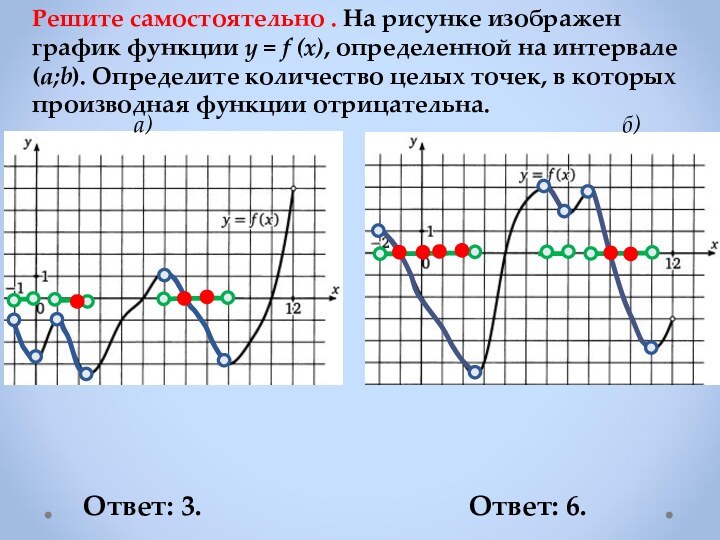
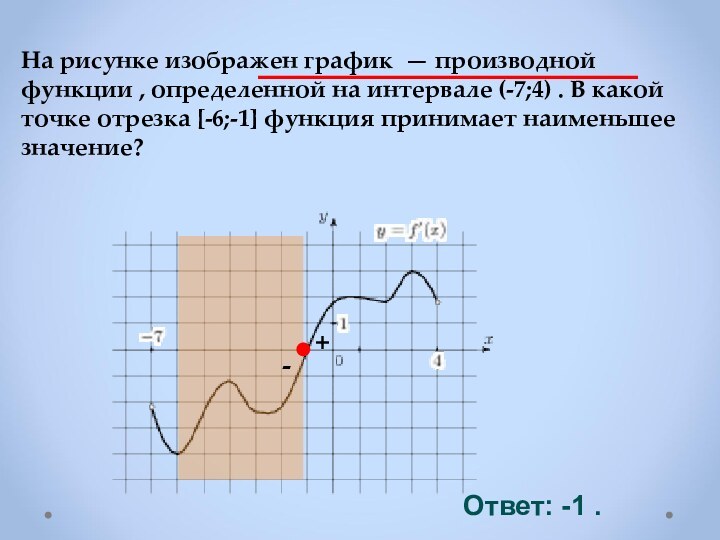
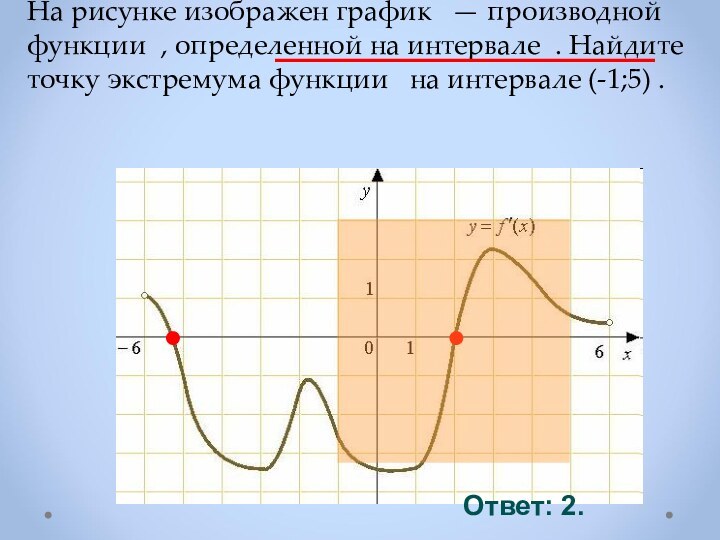
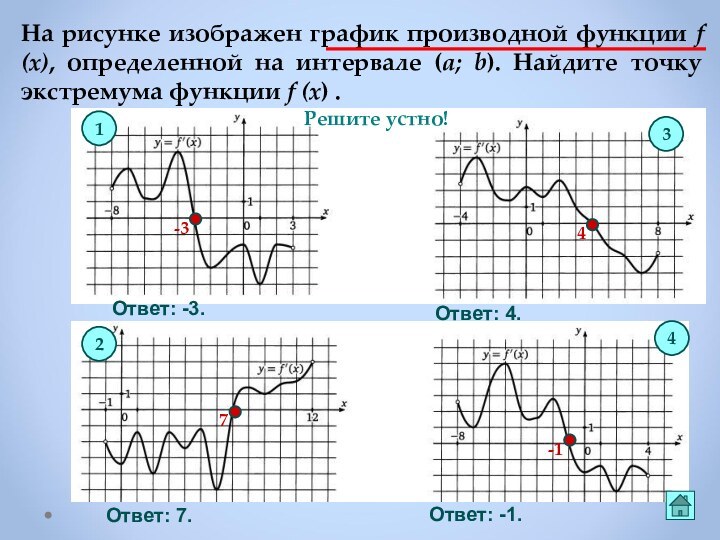
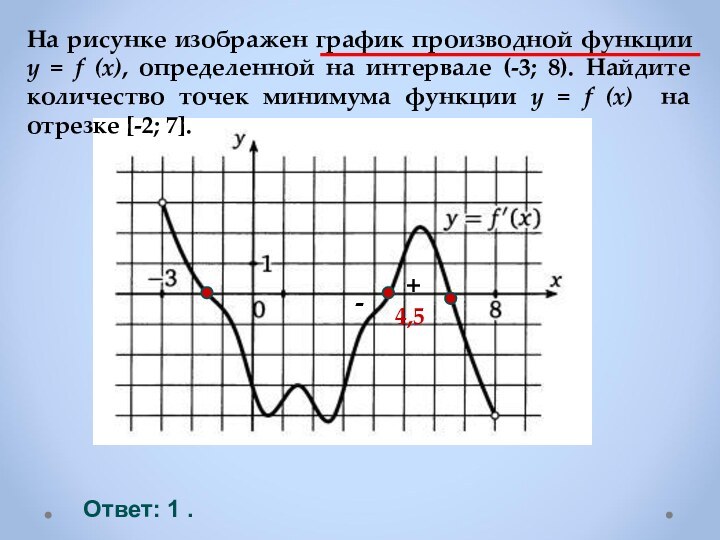
Если в точке х0
производная меняет
знак с минуса на плюс,
то х0 точка минимума
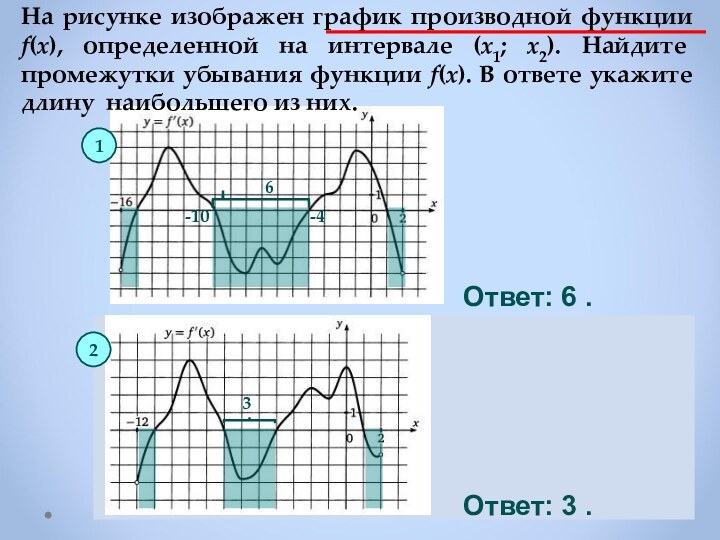
Если f ′(х)< 0 в каждой точке интервала I , то функция убывает на I.