Слайд 2
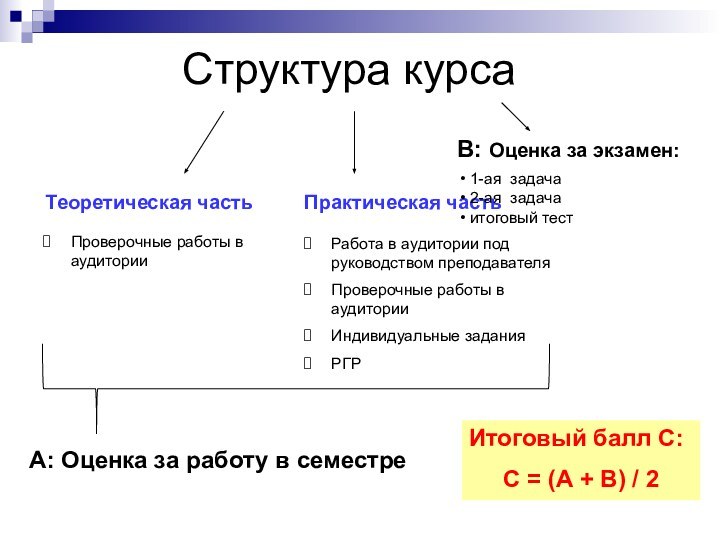
Структура курса
Теоретическая часть
Практическая часть
Работа в аудитории под руководством
преподавателя
Проверочные работы в аудитории
Индивидуальные задания
РГР
В: Оценка за экзамен:
1-ая
задача
2-ая задача
итоговый тест
Проверочные работы в аудитории
А: Оценка за работу в семестре
Итоговый балл С:
С = (А + В) / 2
Слайд 3
«Что необходимо на занятии?»
Учебник (несколько, взять в библиотеке)
Задачник
(авторы: Мошкова Т.В., Тюрина В.А.)
Линейки, «треугольники»
Циркуль
Карандаши (твердые и мягкие)
Тетрадь
формата А4
Ватман (А4, А3)
«Флэшка»
Слайд 4
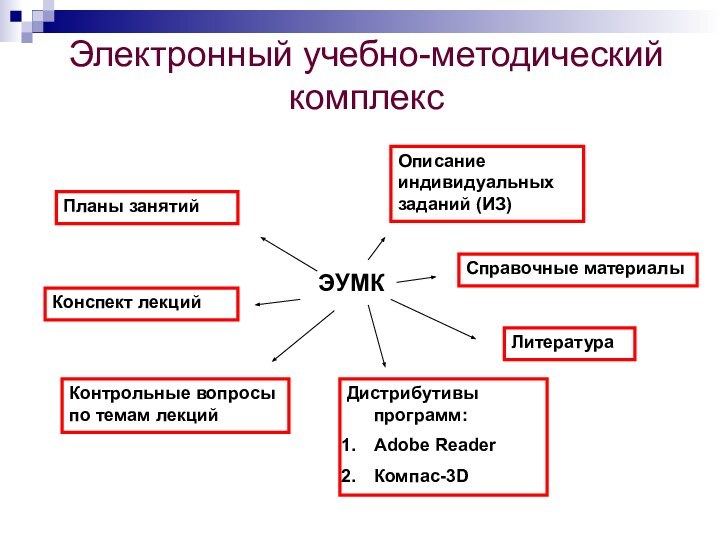
Электронный учебно-методический комплекс
Слайд 5
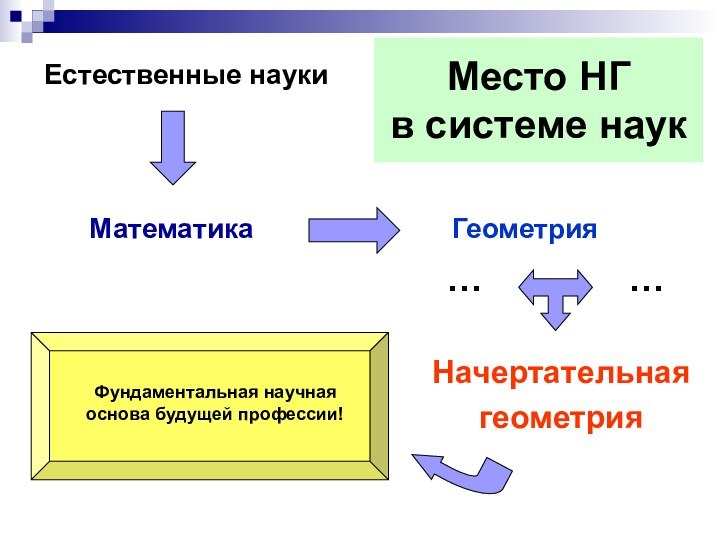
Место НГ
в системе наук
Естественные науки
Математика
Геометрия
Начертательная
геометрия
Слайд 6
Начертательная геометрия – это раздел геометрии,
в котором
изучаются :
Методы построения плоских изображений пространственных
геометрических объектов
Способы решения пространственных геометрических задач на этих изображениях
Слайд 7
Геометрическая модель (фигура) – носитель геометрической информации об
объекте:
учитывает только форму, размеры и расположение предметов;
не учитывает их физических и иных свойств (например, материал, массу, прочность, цвет и т.п.)
Слайд 8
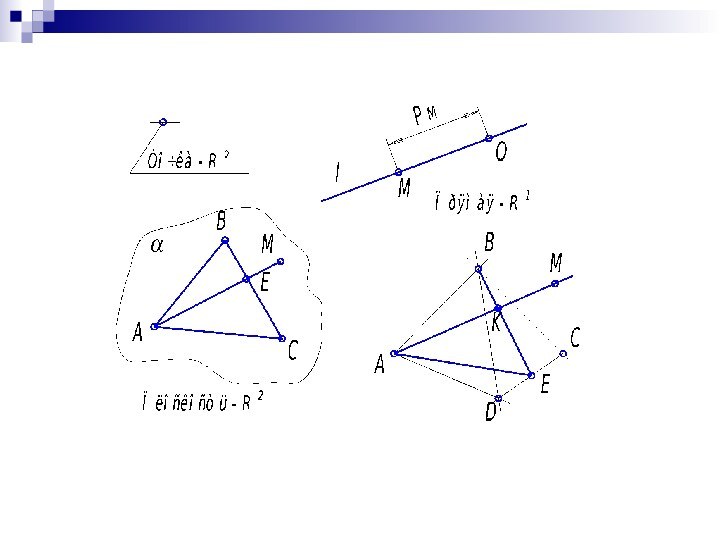
Базовые геометрические фигуры НГ, не имеющие формы:
Точка
- нольмерное пространство R0
Прямая - одномерное пространство R1
Плоскость - двумерное пространство R2
Слайд 9
Математическая модель окружающего нас пространства – линейное 3-х
мерное пространство R3, базовый элемент которого – точка.
Геометрическую фигуру
Ф считают состоящей из точек и определяют как некоторое множество точек U.
U ⊂ R3
Слайд 10
Геометрические фигуры делятся на:
Линейные фигуры
(точка, прямая, плоскость)
Нелинейные
(кривая линия, поверхность)
Составные
(например, многогранник)
Слайд 11
Виды изображений
Можно судить об объекте по
его изображению, если оно обладает следующими свойствами:
Обратимость
Наглядность
Единство условностей
Слайд 12
Обратимость
Свойство, позволяющее однозначно восстанавливать действительную форму и размеры
предмета, а также его положение в пространстве.
Графическое изображение, обладающее
свойством обратимости, называется
чертежом.
Слайд 13
Наглядность
Свойство изображения, дающее возможность вызвать в мозгу зрителя
пространственное представление о предмете.
Элемент наглядности – естественность (особенно
важен для архитектурно-строительной практики).
Желателен для чертежа.
Слайд 14
Единство условностей
Принятые при выполнении изображения условности должны быть
общими для специалистов определенной области знаний.
Установлены законы оформления чертежей
– стандарты (ГОСТ).
Свод таких стандартов называют Единой Системой Конструкторской Документации (ЕСКД).
Слайд 15
ЕСКД в общей системе стандартизации
ЕСКД присвоен код 2.
Внутри
ЕСКД стандарты объединяются по группам, которым присваивается код от
0 до 9.
Например, 3 – общие правила выполнения чертежей.
В каждой группе стандартам присваивается порядковый номер, затем указывается год регистрации стандарта и присваивается наименование.
Например, ГОСТ 2.301-68 Форматы.
Слайд 16
Изображение, самое близкое к естественному, перспектива
Эскиз архитектурно-перспективной декорации.
Художник
П. Гонзаго. Начало XIX века
Слайд 17
Перекресток ул. Б. Покровской и ул. Грузинской
Слайд 18
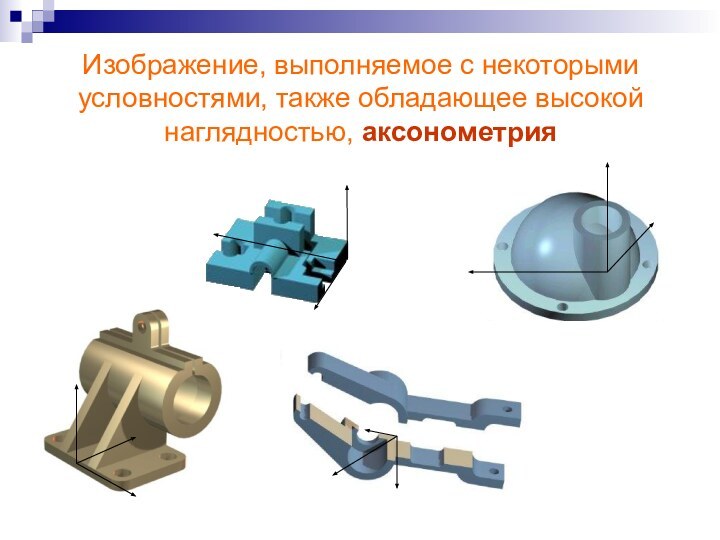
Изображение, выполняемое с некоторыми условностями, также обладающее высокой
наглядностью, аксонометрия
Слайд 19
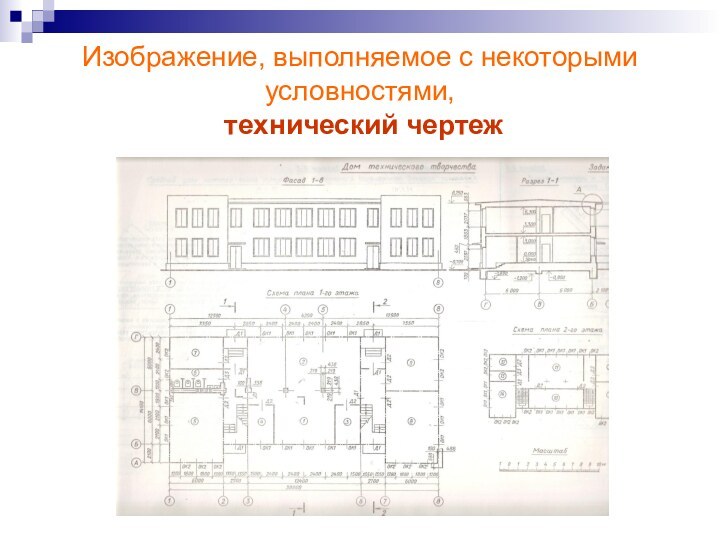
Изображение, выполняемое с некоторыми условностями,
технический чертеж
Слайд 20
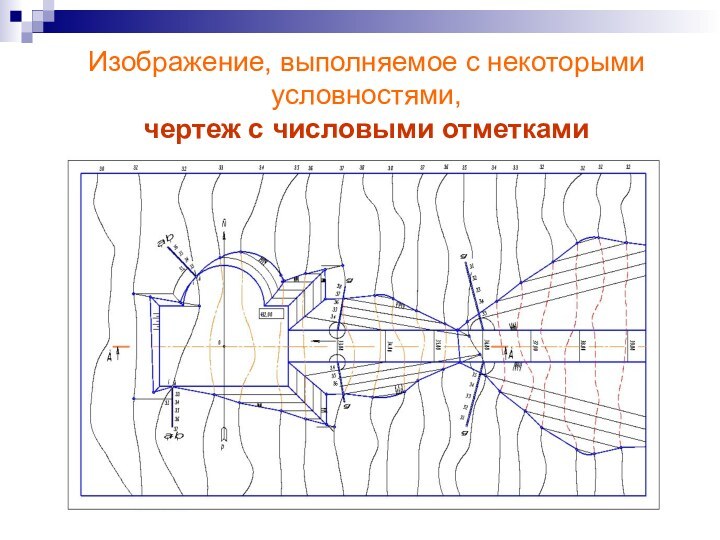
Изображение, выполняемое с некоторыми условностями,
чертеж с числовыми отметками
Слайд 21
Чертеж является
международным графическим языком,
который должен быть
понятен технически
грамотному человеку.
Начертательная геометрия -
грамматика этого языка.
Слайд 22
Для построения изображений геометрических фигур начертательная
геометрия применяет метод проецирования.
Получающиеся при этом изображения
называются
проекционными чертежами.
Слайд 23
Параметры – независимые величины, значения которых
служат для различения элементов некоторого множества между собой.
В геометрических задачах параметры выделяют единственную фигуру
или подмножество фигур
из множества фигур,
соответствующих одному и тому же определению.
Слайд 24
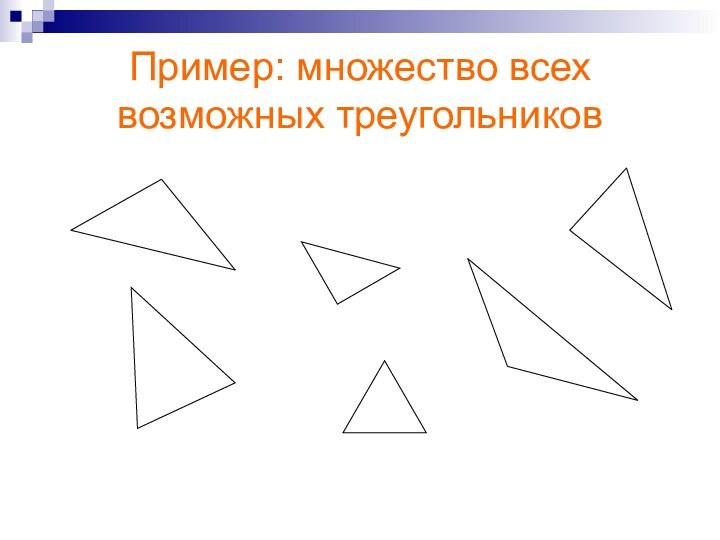
Пример: множество всех возможных треугольников
Слайд 26
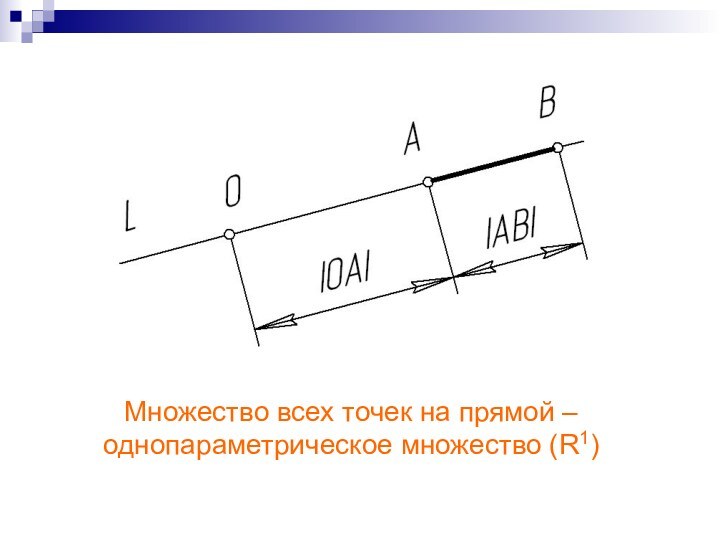
Множество всех точек на прямой –
однопараметрическое множество
(R1)
Слайд 27
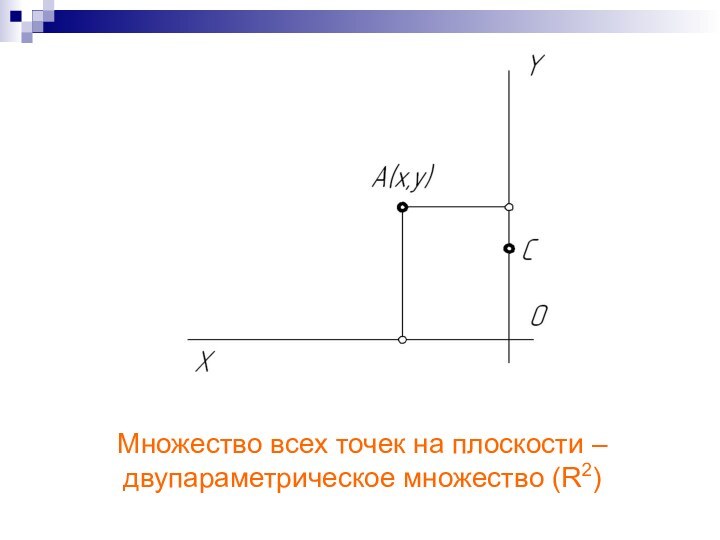
Множество всех точек на плоскости –
двупараметрическое множество
(R2)
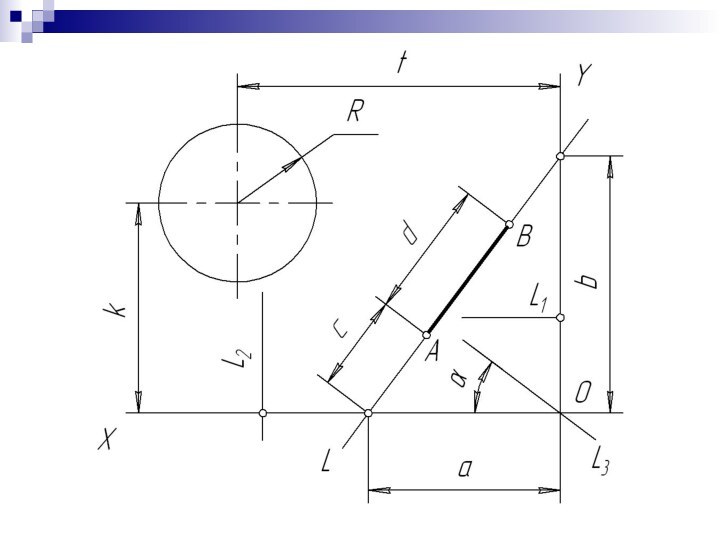
Слайд 30
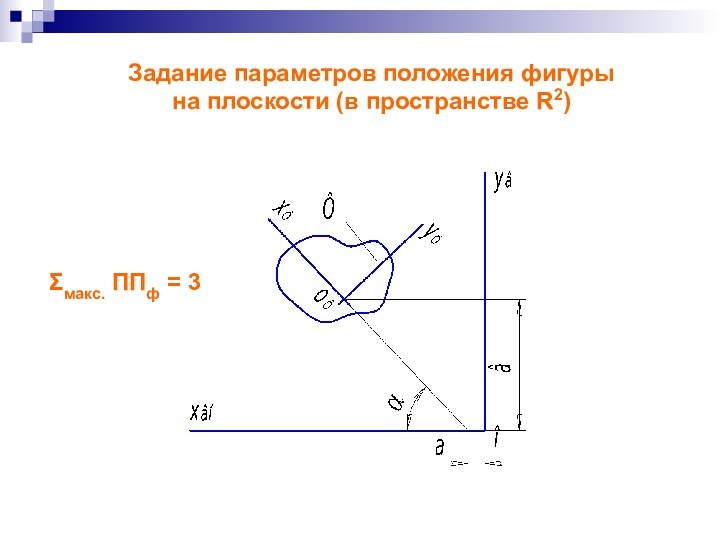
Задание параметров положения фигуры
на плоскости (в пространстве
R2)
Σмакс. ППф = 3
Слайд 31
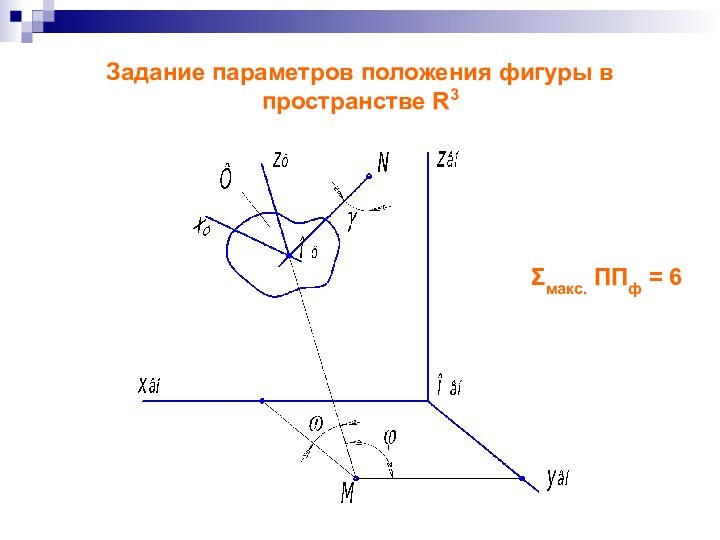
Задание параметров положения фигуры в пространстве R3
Σмакс. ППф
Слайд 33
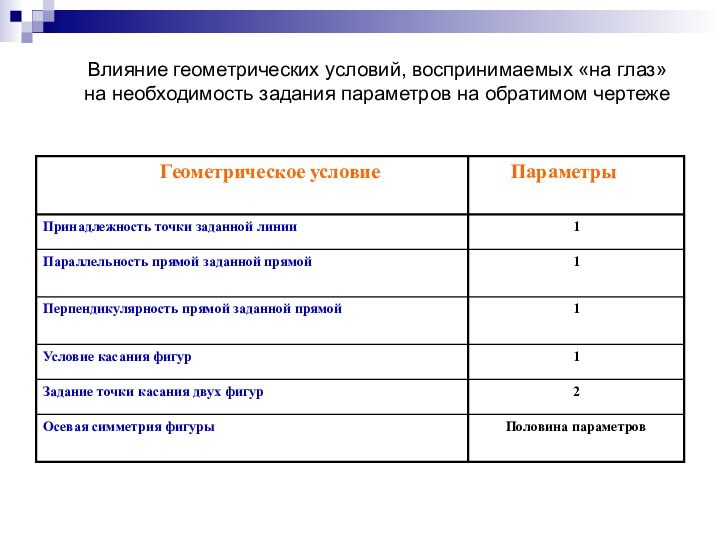
Влияние геометрических условий, воспринимаемых «на глаз»
на необходимость задания
параметров на обратимом чертеже
Слайд 34
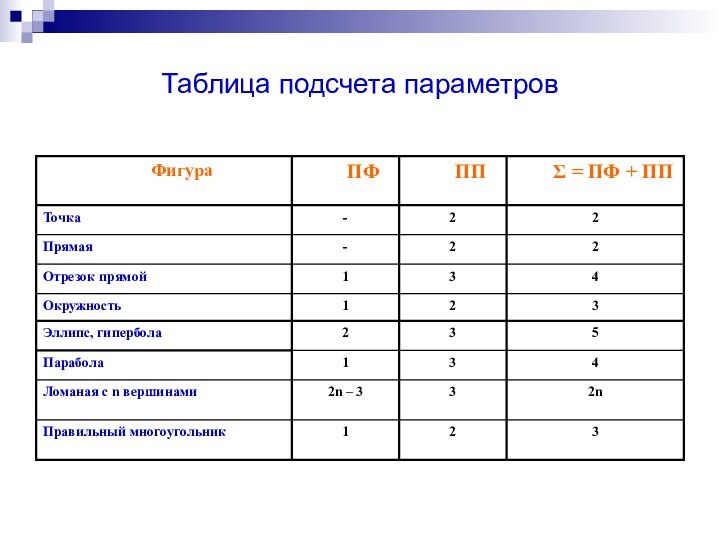
Формула подсчета параметров фигуры:
ΣПФ = ПП + ПФ
- ГУ