Слайд 2
Понятие корреляции появилось в середине XIX века в
работах английских статистиков Ф. Гальтона и К. Пирсона. Этот
термин произошел от латинского "correlatio" - соотношение, взаимосвязь. Понятие регрессии (латинское "regressio" - движение назад) также введено Ф. Гальтоном, который, изучая связь между ростом родителей и их детей, обнаружил явление "регрессии к среднему" - рост детей очень высоких родителей имел тенденцию быть ближе к средней величине.
Теория и методы корреляционного анализа используются для выявления связи между случайными переменными и оценки ее тесноты. Основной задачей регрессионного анализа является установление формы и изучение зависимости между переменными.
Слайд 4
Функция ŷ = f (x1,x2,...,xp),
описывающая зависимость показателя от
параметров, называется уравнением (функцией) регрессии.
Уравнение регрессии показывает ожидаемое значение зависимой переменной при определенных значениях зависимых переменных .
В зависимости от количества включенных в модель факторов Х модели делятся на однофакторные (парная модель регрессии) и многофакторные (модель множественной регрессии).
Слайд 5
В зависимости от
вида функции f(X1, X2,…Xk) модели делятся на линейные и
нелинейные.
Модель множественной линейной регрессии имеет вид:
y i = 0 + 1x i 1 +2x i 2 +…+ k x i k + i (1)
- количество наблюдений.
коэффициент регрессии j показывает, на какую величину в среднем изменится результативный признак , если переменную xj увеличить на единицу измерения, т. е. j является нормативным коэффициентом.
Коэффициент может быть отрицательным. Это означает, что область существования показателя не включает нулевых значений параметров. Если же а0>0, то область существования показателя включает нулевые значения параметров, а сам коэффициент характеризует среднее значение показателя при отсутствии воздействий параметров.
Слайд 6
Анализ уравнения
(1) и методика определения параметров становятся более наглядными, а
расчетные процедуры существенно упрощаются, если воспользоваться матричной формой записи:
Y=Xa+ε (2)
Где – вектор зависимой переменной размерности п 1, представляющий собой п наблюдений значений .
- матрица п наблюдений независимых переменных , размерность матрицы равна п (k+1) . Дополнительный фактор , состоящий из единиц, вводится для вычисления свободного члена. В качестве исходных данных могут быть временные ряды или пространственная выборка.
Слайд 7
k- количество факторов, включенных
в модель.
a — подлежащий
оцениванию вектор неизвестных параметров размерности (k+1) 1;
—ε вектор случайных отклонений (возмущений) размерности п 1. ε отражает тот факт, что изменение будет неточно описываться изменением объясняющих переменных , так как существуют и другие факторы, неучтенные в данной модели.
Слайд 8
k - количество факторов,
включенных в модель.
a —
подлежащий оцениванию вектор неизвестных параметров размерности (k+1) 1;
ε — вектор случайных отклонений (возмущений) размерности п 1. отражает тот факт, что изменение будет неточно описываться изменением объясняющих переменных , так как существуют и другие факторы, неучтенные в данной модели.
Слайд 9
Таким образом,
Уравнение (2) содержит значения неизвестных параметров 0,1,2,…
,k
Эти величины оцениваются на основе выборочных наблюдений, поэтому
полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Модель линейной регрессии, в которой вместо истинных значений параметров подставлены их оценки (а именно такие регрессии и применяются на практике), имеет вид
Слайд 10
где A — вектор оценок
параметров; е — вектор «оцененных» отклонений регрессии, остатки регрессии
е = Y - ХА; —оценка значений Y, равная ХА.
Построение уравнения регрессии осуществляется, как правило, методом наименьших квадратов (МНК), суть которого состоит в минимизации суммы квадратов отклонений фактических значений результатного признака от его расчетных значений, т.е.:
Слайд 11
Формулу для вычисления параметров
регрессионного уравнения по методу наименьших квадратов приведем без вывода
Для того чтобы регрессионный анализ, основанный на обычном методе наименьших квадратов, давал наилучшие из всех возможных результаты, должны выполняться следующие условия, известные как условия Гаусса – Маркова.
Слайд 12
Первое условие. Математическое ожидание
случайной составляющей в любом наблюдении должно быть равно нулю.
Второе условие означает, что дисперсия случайной составляющей должна быть постоянна для всех наблюдений. Эта постоянная дисперсия обычно обозначается , или часто в более краткой форме , а условие записывается следующим образом:
Выполнимость данного условия называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью, (непостоянством дисперсии отклонений).
Слайд 13
Третье условие предполагает отсутствие
систематической связи между значениями случайной составляющей в любых двух
наблюдениях. В силу того, что , данное условие можно записать следующим образом:
Возмущения не коррелированны (условие независимости случайных составляющих в различных наблюдениях). Это условие означает, что отклонения регрессии (а значит, и сама зависимая переменная) не коррелируют.
Четвертое условие состоит в том, что в модели (1) возмущение (или зависимая переменная ) есть величина случайная, а объясняющая переменная - величина неслучайная. Если это условие выполнено, то теоретическая ковариация между независимой переменной и случайным членом равна нулю.
Слайд 14
КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ В MS EXCEL
Создайте файл исходных данных
в MS Excel (например, таблица 2)
Построение корреляционного поля
Для построения
корреляционного поля в командной строке выбираем меню Вставка/ Диаграмма. В появившемся диалоговом окне выберите тип диаграммы: Точечная; вид: Точечная диаграмма, позволяющая сравнить пары значений (Рис. 5).
Слайд 15
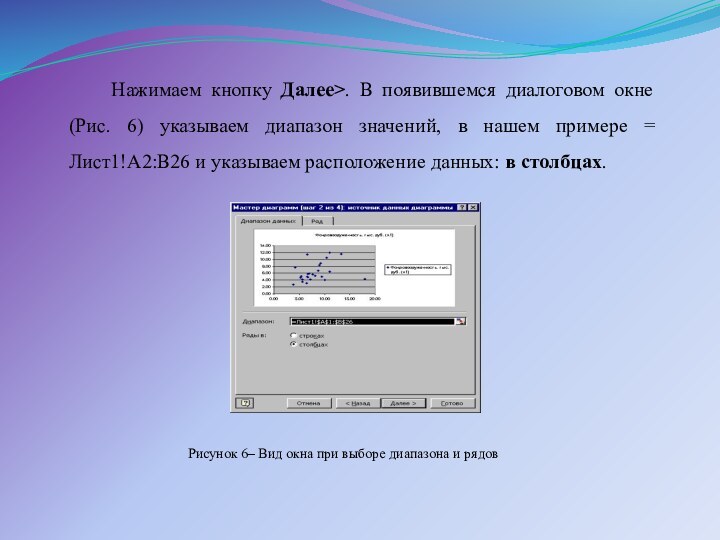
Нажимаем кнопку Далее>. В появившемся диалоговом окне (Рис.
6) указываем диапазон значений, в нашем примере = Лист1!A2:B26
и указываем расположение данных: в столбцах.
Рисунок 6– Вид окна при выборе диапазона и рядов
Слайд 16
Нажимаем кнопку Далее>. В следующем диалоговом окне (рис.
7) указываем название диаграммы, наименование осей. Нажимаем кнопку Далее>,
и Готово.
Рисунок 7 – Вид окна, шаг 3.
Таким образом, получаем корреляционное поле зависимости y от x. Далее добавим на графике линию тренда, для чего выполним следующие действия:
Слайд 17
В области диаграммы щелкнуть левой кнопкой мыши по
любой точке графика, затем щелкнуть правой кнопкой мыши по
этой же точке. Появляется контекстное меню (рис. 8).
Рисунок 8 – Вид окна, шаг 4
В контекстном меню выбираем команду Добавить линию тренда.
В появившемся диалоговом окне выбираем тип графика (в нашем примере линейная) и параметры уравнения, как показано на рисунке 9.
Слайд 18
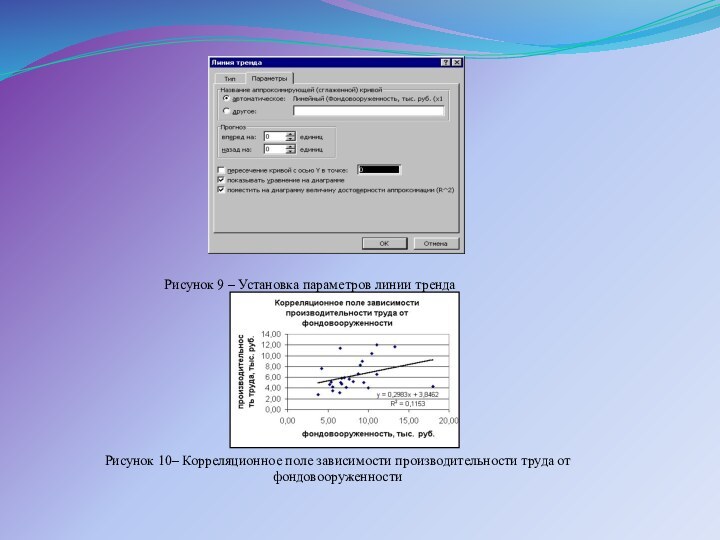
Рисунок 9 – Установка параметров линии тренда
Рисунок 10–
Корреляционное поле зависимости производительности труда от фондовооруженности
Слайд 19
Аналогично строим корреляционное поле зависимости производительности труда от
коэффициента сменности оборудования. (рисунок 11).
Рисунок 11 – Корреляционное поле
зависимости производительности труда
от коэффициента сменности оборудования
Построение корреляционной матрицы.
Для построения корреляционной матрицы в меню Сервис выбираем Анализ данных.
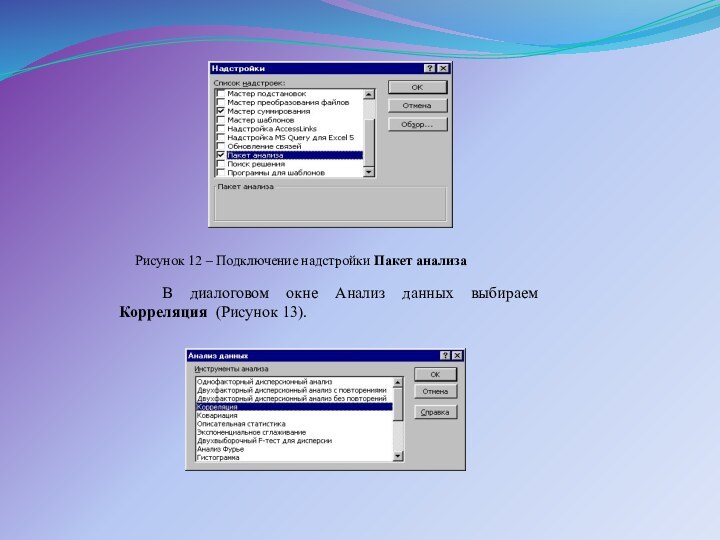
С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Для этого необходимо проверить доступ к пакету анализа. В главном меню последовательно выберите Сервис/ Надстройки. Установите флажок Пакет анализа (Рисунок 12)
Слайд 20
Рисунок 12 – Подключение надстройки Пакет анализа
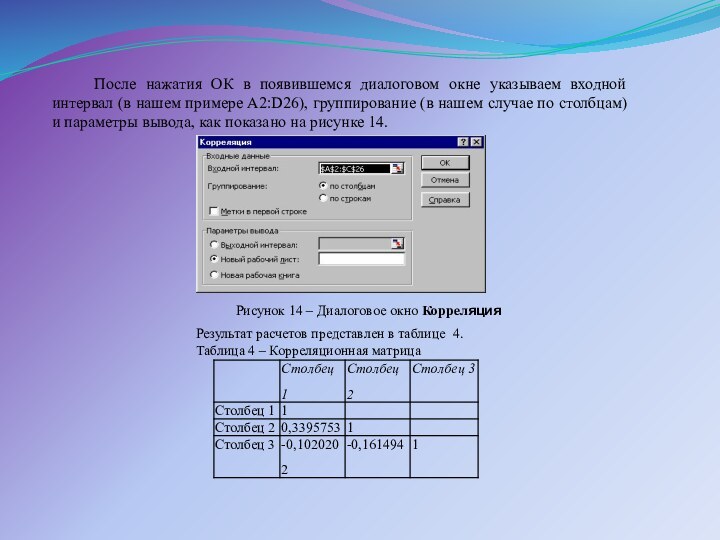
В диалоговом
окне Анализ данных выбираем Корреляция (Рисунок 13).