Слайд 2
Задача устойчивых паросочетаний была частично сформулирована в 1962
году, когда два экономиста-математика,
Дэвид Гейл и Ллойд Шепли, задались
вопросом:
Можно ли спланировать процесс поступления в колледж (или приема на работу), который был бы саморегулируемым (self-enforcing)?
Слайд 3
Решение было опубликовано в 1962 году в журнале
American Mathematical Monthly в статье под названием «Поступление в
колледж и стабильность браков».
Элвин Рот разработал очень много практических механизмов, основанных на алгоритме Гейла-Шелли.
Ллойд Шепли и Элвин Рот в 2012 году получили Нобелевскую премию по экономике «За теорию стабильного распределения и практики устройства рынков».
Слайд 4
Примеры механизмов, которые были внедрены:
Распределение врачей по больницам
Распределение
интернов по больницам
Набор спортсменов в команды
Набор стажеров в компании
Наем
клерков в суды
Подбор школ для детей
Доноры и реципиенты
Слайд 5
Группа студентов колледжа начинает подавать заявки в компании
на летнюю практику.
В процессе обработки заявок важно взаимодействие двух
разных сторон: компаний (нанимателей) и студентов (кандидатов).
Каждый кандидат упорядочивает список компаний в порядке своих предпочтений.
Каждая компания - после поступления заявок - формирует свой порядок предпочтений для кандидатов, подавших заявки.
На основании этих предпочтений компании обращаются с предложениями к некоторым из своих кандидатов.
Кандидаты решают, какое из полученных предложений стоит принять.
Слайд 6
Возможные сбои
Радж только что принял предложение от крупной
телекоммуникационной компании CluNet. Через несколько дней начинающая компания WebExodus,
которая тянула с принятием нескольких окончательных решений, связывается с Раджем и тоже предлагает ему летнюю практику. Вообще-то, с точки зрения Раджа, вариант с WebExodus предпочтительнее CluNet - скажем, из-за непринужденной атмосферы и творческого азарта. Этот поворот заставляет Раджа отказаться от предложения CluNet и пойти в WebExodus. Лишившись практиканта, CluNet предлагает работу одному из запасных кандидатов, который мгновенно отменяет свое предыдущее согласие на предложение мегакорпорации Babelsoft.
Слайд 7
Возможные сбои
Подруге Раджа по имени Челси было назначено
отправиться в Babelsoft. Но услышав историю Раджа, она звонит
в WebExodus и говорит: «Знаете, я бы предпочла провести это лето в вашей фирме, а не в Babelsoft». Отдел кадров WebExodus охотно верит; более того, заглянув в заявку Челси, они понимают, что она перспективнее другого студента, у которого уже запланирована летняя практика. И если компания WebExodus не отличается особой деловой принципиальностью, она найдет способ отозвать свое предложение другому студенту и возьмет Челси на его место.
Слайд 8
Основная проблема
Процесс не является саморегулируемым.
Если участникам разрешено произвольно
действовать, исходя из их собственных интересов, весь процесс может
быть нарушен.
Многие участники - как кандидаты, так и наниматели - могут оказаться недовольны как самим процессом, так и его результатом.
Слайд 9
Формулировка задачи с устойчивыми результатами
Можно ли для имеющегося
набора предпочтений по кандидатам и нанимателям распределить кандидатов по
нанимателям так, чтобы для каждого нанимателя E и каждого кандидата A, который не был принят на работу к E, выполнялось по крайней мере одно из следующих двух условий?
Каждый из кандидатов, принятых E на работу, с его точки зрения, предпочтительнее A.
С точки зрения A, его текущая ситуация предпочтительнее работы на нанимателя E.
Слайд 10
За десять лет до работы Гейла и Шепли
очень похожая задача использовалась Национальной программой распределения студентов-медиков по
больницам.
Более того, эта система с относительно незначительными изменениями продолжает применяться и в наши дни.
Другие источники происхождения задачи
Слайд 11
Каждый из n кандидатов подает заявки в каждую
из n компаний, а каждая компания хочет принять на
работу одного кандидата.
Упрощенная постановка задачи
Слайд 12
Имеется множество M = {m1, ..., mn} из
n мужчин и множество W = {w1, ..., wn
} из n женщин.
Паросочетание (марьяж) S представляет собой множество пар из M × W, обладающее тем свойством, что каждый элемент M и каждый элемент W встречается не более чем в одной паре в S.
Идеальным паросочетанием S' называется паросочетание, при котором каждый элемент M и каждый элемент W встречается ровно в одной паре из S'
Частный случай задачи
Слайд 13
Каждый мужчина m ∈ M формирует оценки всех
женщин; мы говорим, что m предпочитает w женщине w',
если m присваивает w более высокую оценку, чем w'.
Мы будем называть упорядоченную систему оценок m его списком предпочтений.
«Ничьи» в оценках запрещены.
Аналогичным образом каждая женщина назначает оценки всем мужчинам.
Понятие предпочтений
Слайд 14
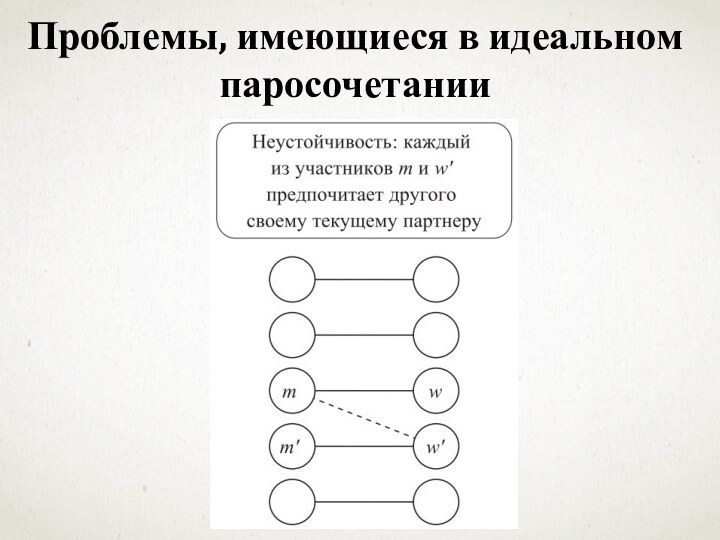
Проблемы, имеющиеся в идеальном паросочетании
Слайд 15
Цель: создать паросочетание без неустойчивых пар.
Паросочетание S называется
устойчивым, если оно (1) идеально и (2) не содержит
неустойчивости в отношении S.
Вопросы:
Существует ли устойчивое паросочетание для каждого набора списков предпочтений?
Можно ли эффективно построить устойчивое паросочетание для имеющегося списка предпочтений (если оно существует)?
Слайд 16
Мужчины: {1, 2}
Женщины: {a, b}
Предпочтения:
Идеальное, но
неустойчивое
паросочетание
устойчивое
паросочетание
Пример 1
Слайд 17
Мужчины: {1, 2}
Женщины: {a, b}
Предпочтения:
1-ое
устойчивое
паросочетание
2-ое
устойчивое
паросочетание
Пример 2
Слайд 18
Мужчины: {1, 2, 3, 4, 5}
Женщины: {a, b,
c, d, e}
Предпочтения:
Мужчины:
Женщины:
Пример 3
Слайд 19
Мужчины делают предложения, а женщины выбирают.
Шаг 1. Начальные
предложения. Мужчины делают предложения (первый столбец матрицы предпочтений), женщины
в соответствии с приоритетом выбирают.
Слайд 20
Шаг 2. Отвергнутые мужчины делают новые предложения (второй
столбец матрицы предпочтений).
Слайд 21
Шаг 3. Настойчивый мужчина 1 делает очередное предложение
женщине a и отвергнут ею.
Слайд 22
Шаг 4. И вновь мужчина 1. Его предложение
женщиной e принято, а мужчина 4 ею отвергнут.
Слайд 23
Шаг 5. Отвергнутый мужчина 4 делает новое предложение.
Слайд 24
Шаг 6. Новое предложение мужчины 4.
В итоге получаем
устойчивое паросочетание:
1 → e, 2 → a, 3 →
b, 4 → d, 5 → c
Слайд 25
Предложения делают женщины, а мужчины осуществляют выбор.
Шаг 1.
Начальные предложения женщин.
Слайд 26
Шаг 2. Отвергнутые женщины делают новые предложения.
Получили устойчивое
паросочетание, причем оно совпадает с тем, когда предложения делали
мужчины, а женщины выбирали.
Слайд 27
Глобальные структуры данных
man, women : Array
[1..n, 1..n] Of Integer; {Матрицы предпочтений}
indexMan : Array
[1.. n] Of Integer; {Номер предложения i-го мужчины}
married : Array [1.. n] Of Integer; {Результат, married[i] определяет номер мужчины, с которым женщина i сочетается законным браком}
freeman : Array [1..n] Of Boolean; {Признак занятости мужчин. Если freeman[i]=True, то мужчина с номером i свободен}
Слайд 28
Начальная инициализация данных:
For i := 1 To n
Do Begin
married[i] := -1; {Женщины не заняты}
indexMan[i]
:= 1; {Каждый мужчина делает предложение первой женщине из своего списка предпочтений}
freeMan[i] := True; {Мужчины свободны}
End;
Слайд 29
Основная логика:
Procedure Solve;
var i, cw : Integer;{i
- № мужчины, cw - № женщины}
Begin
While
Not Result Do {Пока не найдено паросочетание}
For i := 1 To n Do
If freeMan[i] Then Begin {i-ый мужчина свободен}
cw := man[i, indexMan[i]];
WriteLn('мужчина ', i, ' делает предложение ', cw, ' женщине');
If (married[cw] = -1) Then Begin {Женщина свободна}
married[cw] := i;
freeMan[i] := False;
End
Else SelectW(i,cw); {Женщина занята и вынуждена делать выбор}
End;
End;
Слайд 30
Проверка того, что найдено устойчивое паросочетание на этих
структурах данных осуществляется подсчетом количества сформировавшихся пар. Если оно
равно значению n, то паросочетание найдено.
Function Result : Boolean;
Var i, k : Integer;
Begin
k := 0;
For i := 1 To n Do
If (married[i] <> -1) Then k := k+1;
If k = n Then Result := True
Else Result := False;
End;
Слайд 31
Логика процедуры выбора женщины:
Идем по приоритетам женщины cw
и ищем, кто встретится раньше: ее жених на данный
момент или сделавший только что предложение i-ый мужчина.
Procedure SelectW(i, cw: Integer);
{i - № мужчины, cw - № женщины}
Var j : Integer;{№ приоритета у женщины cw}
pp : Boolean;{женщина cw сделала выбор}
Begin
j := 1;
pp := False;
End;
Цикл по j
Begin
If (women[cw, j] = married[cw]) Then Begin
{жених в приоритете}
indexMan[i] := indexMan[i] + 1; {i-му мужчине надо выбирать следующую женщину по его приоритету}
pp := True;
end
Else If (women[cw, j] = i) Then Begin {Женщина отдает предпочтение мужчине с номером i}
indexMan[married[cw]] := indexMan[married[cw]] + 1; {жениху женщины cw надо выбирать следующую женщину по его приоритету}
freeMan[married[cw]] := True; {жених становится свободным}
freeMan[i] := False; {i-ый мужчина становится занятым}
married[cw] := i;{i становится женихом для cw}
pp := True;
End;
j :=j + 1;
End;
Слайд 33
Мужчины: {1, 2, 3}
Женщины: {a, b, c}
Предпочтения:
Мужчины:
Женщины:
Задача 1

























![Задача о поиске устойчивых паросочетаний. (Лекция 11) Глобальные структуры данных man, women : Array [1..n, 1..n] Of Integer;](/img/tmb/15/1466500/d8b8af5bc3a79f28d8cab5f138c2fad5-720x.jpg)
![Задача о поиске устойчивых паросочетаний. (Лекция 11) Начальная инициализация данных:For i := 1 To n Do Begin married[i] :=](/img/tmb/15/1466500/0ab316b9f68e9c33989fdf50d092e616-720x.jpg)